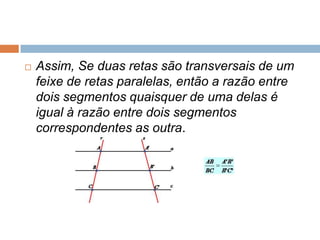
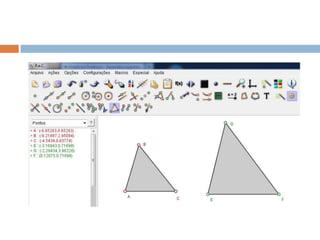
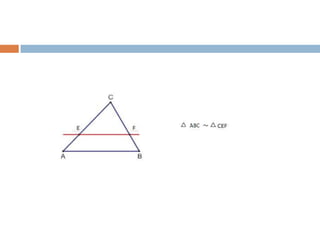
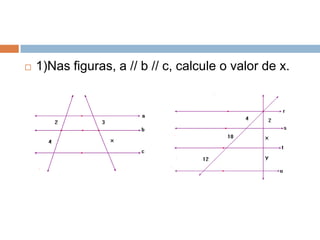
Este documento propõe uma aula interativa sobre o Teorema de Tales e proporcionalidade utilizando o programa Régua e Compasso. Os alunos irão construir figuras geométricas e responder perguntas para descobrir que as razões entre segmentos mudam proporcionalmente quando retas paralelas são cortadas por transversais. O documento fornece instruções detalhadas para a aula.

1. TEOREMA DE TALES
E
PROPORCIONALIDADE
POR VIVIANE DAS GRAÇAS DOS SANTOS
INFORMÁTICA EDUCATIVA I
TUTOR: ANDRÉ TENÓRIO

2. 

Conteúdos
- Geometria
Proporcionalidade.
9° Ano
Tempo estimado
De 04a 06 aulas de 50 minutos.


Material necessário:
Folha A4 para anotações
computador com Rec ( régua e compasso) e internet para a
atividades complementar.
Notebook e data show.

3. 
Justificativa: Esta aula é uma proposta interativa
e diferenciada do ensino de
Geometria, possibilitando a criação de um
ambiente favorável à aprendizagem.

Objetivos:
Utilizando conteúdos prévios como
razão, proporção, retas paralelas e transversais o
Teorema de Tales será apresentado com a
utilização do programa régua e
compasso, ReC, assim como suas implicações e
aplicações em situações problemas.

4. 

A aula será ministrada num laboratório de informática
com os alunos dispostos em dupla ou
individualmente. Professor deverá dar as instruções,
utilizando o data-show para possibilitar o
entendimento e a visualização das ferramentas do
software.
O passo a passo é fundamental para os alunos que
terão um primeiro contato com o software.



A primeira parte é experimental, sem uma introdução
do conteúdo. O professor orientará os alunos nas
construções. Em seguida os alunos farão anotações
em uma folha A4, respondendo as questões pedidas.

5. 
Ação 01-Utilizando o programa Régua e
Compasso siga os passos.


Nessa ação serão poderemos utilizar as
ferramentas:




Traçar 03 retas paralelas e 02 transversais.


Nomear os pontos de interseção entre elas (A, B,
C, D, E e F).

6. 



Questão 01-Determinar as medidas dos
segmentos AB, BC, DE e EF formados.
Questão 02-Determinar as razões: AB/BC,
DE/EF.
Exemplos da construção:

8. 
Questão 03-Analisando a construção, o que
se pode observar com os resultados obtidos?


Ação 02: Mova o ponto A

10. 
Anote os valores encontrados.


Questão 04-O que se pode observar sobre os valores
das medidas dos segmentos AB, BC, DE e EF?


Questão 05- O que ocorreu com as razões: AB/BC,
DE/EF.


Ação 03: Faça o mesmo para o ponto C


O professor pode pedir que os alunos descrevam
suas conclusões. Espera-se que ele observe as
razões mudam proporcionalmente.

11. 

A seguir faz-se a exibição de um vídeo que
aborda um pouco parte histórica do conteúdo
a ser estudado, formalizando-se o Teorema
Tales as ideia que norteiam o princípio da
proporcionalidade.


<http://www.youtube.com/watch?v=cWkU6fGo
YA8

12. 
Assim, Se duas retas são transversais de um
feixe de retas paralelas, então a razão entre
dois segmentos quaisquer de uma delas é
igual à razão entre dois segmentos
correspondentes as outra.

13. 
Vimos no vídeo que os triângulos formados
pelas alturas e sombras são semelhantes.
Façamos então e próxima construção:



Ação 04-Desenhe os triângulos ABC e EFG
utilizando a ferramenta
Exemplo da construção:

15. 


Questão 06-Verifique as medidas dos lados AB,
AC, BC, EF, FG e EG.
Questão 07-Verifique as razões: Determine as
razões AB/EG, AC/EF e BC/GF.
Questão 08-Os lados são proporcionais?
Justifique.


Ação 05- Construa o triângulo ABC


Trace uma paralela ao lado AB formando um
triângulo ECF

16. 

Nomeie os pontos determinados.
Represente a medida dos lados dos triângulos
obtidos.



Questão 09-Determine as razões
CE/CF, EA/FB e compare essa construção
com a anterior.
Questão 10-Os triângulos são semelhantes?


Exemplos da construção:

18. 
Formalizando a ação 05.



Se uma reta é paralela a um dos lados de um
triângulo e intercepta os outros dois em pontos
distintos, então o triângulo que ela determina
é semelhante ao primeiro.

20. 
Atividade Complementar:


Segue em:

http://objetoseducacionais2.mec.gov.br/bitstre
am/handle/mec/841/alturas.swf?sequencs=7
dois desafios para a determinação da altura
do colosso e da pirâmide de Quéops
utilizando os conteúdos aprendidos sob forma
de

21. 
No 1° desafio, peça aos alunos que façam a
comparação com todos os objetos
disponibilizados.

22. 
No 2° desafio, os alunos poderão alterar o
horário (mais cedo ou mais tarde). Sugira que
eles o façam e discutam o que se Poe
observar com essas alterações.

23. 
A verificação da aprendizagem se dará ao
longo das ações propostas, das anotações
feitas pelo aluno e por situações que
envolvam o tema estudado.


Exemplos de exercícios:

24. 
1)Nas figuras, a // b // c, calcule o valor de x.

25. 
4) Uma estátua projeta uma sombra de 8 m no
mesmo instante que seu pedestal projeta uma
sombra de 3,2 m. Se o pedestal tem 2 m de
altura, determinar a altura da estátua.

26. 
Referências:




ANDRINI, Álvaro e VASCONCELOS, Maria José. Praticando matemática,
8º série. 1º edição, São Paulo: Editora do Brasil, 2002.
GIOVANNI JUNIOR, José Ruy. A conquista da matemática, 8º série. São
Paulo: FTD, 2009.
Mathias, Carlos Eduardo. Programa de Geometria Dinâmica Plana: Uma
apresentação através do Rec. Material de Estudo.


Sites




http://www.brasilescola.com/matematica/teorema-tales.htm. Acesso:
Outubro 2013
http://www.youtube.com/watch?v=cWkU6fGoYA8> Acesso: Outubro 2013.

27. 
http://objetoseducacionais2.mec.gov.br/bitstream/handle/mec/841/alturas.swf?seque
ncs=7 Acesso: outubro 2013.


http://www.professores.uff.br/hjbortol/car/


Tutorial01http://www.youtube.com/watch?v=pv5AbSoFVwA. Acesso: Setembro
2013.


Tutorial02http://www.youtube.com/watch?v=lg-Xdt0Wf8Y Acesso: Setembro 2013.


Tutorail03http://www.youtube.com/watch?v=qgzXKiCCOrY Acesso: Setembro 2013.



Tutorial04http://www.youtube.com/watch?v=8rkygVRzaOk Acesso: Setembro 2013.