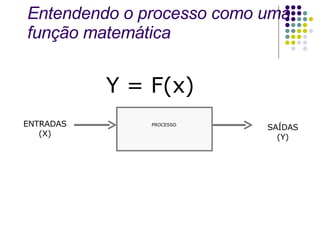
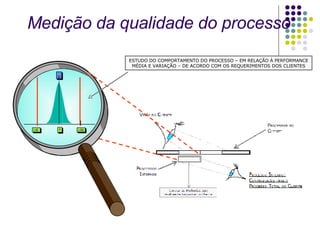
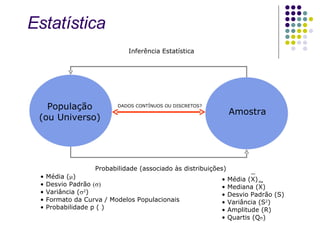
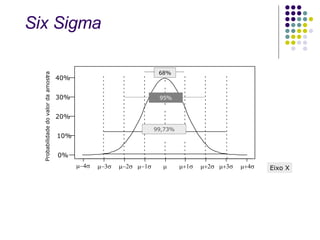
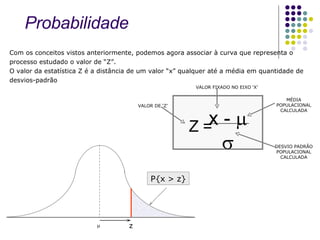
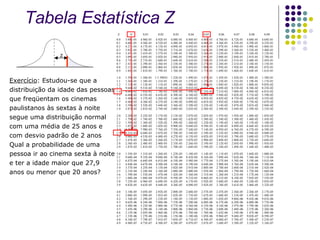
O documento discute conceitos estatísticos como média, desvio padrão e distribuição normal que são usados na metodologia Six Sigma para analisar processos e identificar oportunidades de melhoria. É apresentado um exemplo numérico ilustrando como calcular a probabilidade de um valor estar em determinada faixa de uma distribuição normal.
![Six Sigma MSc. Luiz Barboza [email_address]](https://image.slidesharecdn.com/sixsigma-1222051362336643-9/75/Sixsigma-1-2048.jpg)




![Six Sigma MSc. Luiz Barboza [email_address]](https://image.slidesharecdn.com/sixsigma-1222051362336643-9/85/Sixsigma-35-320.jpg)