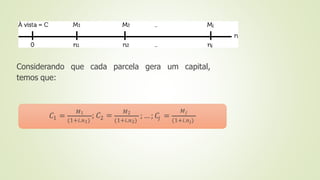
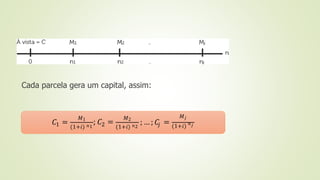
O documento apresenta os principais conceitos de matemática financeira, incluindo capital, juros, montante, juros simples, juros compostos e séries de pagamentos. Juros simples são calculados sobre o capital inicial, enquanto juros compostos são calculados sobre o montante do período anterior. Séries permitem o pagamento parcelado calculando o capital a partir de cada prestação futura.

1. MATEMÁTICA
FINANCEIRA
AULA 1

2. Introdução
A matemática financeira possui diversas aplicações no
nosso sistema econômico. Podemos encontrá-la em
situações do dia-a-dia como:
• Ao financiar um carro;
• Realizar empréstimos;
• Comprar no crediário ou no cartão de crédito.

3. Capital (C)
O capital
disponível
é a quantidade de recurso
ou exigido no ato de uma
financeiro
operação
financeira, compra ou aplicação.
O capital também é denominado como Valor
Presente (VP) e Valor Atual (VA).

4. Juros (J)
• São as compensações financeiras nas operações
realizadas, representando um acréscimo.
• Pode ser o rendimento de uma aplicação financeira, o
valor referente ao atraso no pagamento de uma
prestação ou também uma quantia paga pelo
empréstimo de um capital.

5. Montante (M)
Montante é a soma do Capital com os juros. O montante
também é conhecido como Valor Futuro.
Em língua inglesa, usa-se Future Value,
indicado nas calculadoras financeiras pela
tecla FV.

6. Juros Simples
O juro simples é calculado sempre sobre o valor do capital
inicial. Os juros de cada período são obtidos multiplicando
a taxa de juros (i) pelo capital (C) e pelo tempo da
aplicação (n)
Obs.: o valor do juro será o mesmo em todos os períodos
(n).
𝑱 = 𝑪. 𝒊. 𝒏

7. Exemplo
 Maria emprestou R$ 1500,00 para pagar após 4 meses, com uma taxa de 2% a. m. no
regime de juros simples. Quanto Maria pagará de juros?
 2
100
𝐶 = 1500 𝑛 = 4 𝑖 = 2%𝑎. 𝑚 = = 0,02
𝐽 = 𝐶. 𝑖. 𝑛
𝐽 = 1500.0,02.4
𝐽 = 120,00

8. Taxa equivalente em Juros Simples
Considerando inicialmente o período comercial, em que 1
mês = 30 dias e 1 ano = 360 dias, temos que:
• Quando a taxa for apresentada numa referência maior
que a solicitada, deverá dividir pela proporção da
referência menor com relação à maior;
• Quando menor, multiplica-se.

9. Montante ou valor futuro
O montante (M) ou valor futuro (VF) – corresponde ao
capital (C) mais o juro (J) produzido em certo período (n).
𝑀 = 𝐶 + 𝐽
𝑀 = 𝐶 + 𝐶. 𝑖. 𝑛
𝑀 = 𝐶(1 + 𝑖. 𝑛)

10. Séries de juros simples
𝑀 = 𝐶(1 + 𝑖. 𝑛) 𝐶 =
𝑀
(1 + 𝑖. 𝑛)
Cada parcela ou prestação são
pequenos Montantes (M).

11. Considerando que cada parcela gera um capital,
temos que:
1
𝐶 =
𝑀1
(1+𝑖.𝑛1) 2
; 𝐶 =
𝑀2
(1+𝑖.𝑛2) 𝑗
; … ; 𝐶 =
𝑀𝑗
(1+𝑖.𝑛𝑗)

12. Logo:
Então:
Assim:
𝐶 = 𝐶1 + 𝐶2 + ⋯ + 𝐶𝑗
𝐶 =
𝑀1
(1 + 𝑖. 𝑛1)
+
𝑀2
(1 + 𝑖. 𝑛2)
+ ⋯ +
𝑀𝑗
(1 + 𝑖. 𝑛𝑗
)
𝑗
𝐶 = ෍
𝑗=1
𝑀𝑗
(1 + 𝑖. 𝑛𝑗 )

13. Em uma situação em que trabalhamos com
pagamento de entrada (E), teremos:
𝑗
𝑀𝑗
𝐶 = 𝐴𝑉 − 𝐸 = ෍
(1 + 𝑖. 𝑛𝑗 )
𝑗=1
𝐶 = 𝐴𝑉 − 𝐸

14. Juros Compostos
O Juro composto é calculado sobre o montante relativo ao
período anterior (CRESPO, 2010, p. 153). Assim, os juros
são incorporados, a cada período de capitalização, ao
principal.
Onde:
𝑖: taxa de juros
𝑛: prazo da operação financeira
𝑀 = 𝐶. (1 + 𝑖) 𝑛

15. Taxa equivalente em juros compostos
Em que 𝑎 é o período
e 𝑝 o período pedido ou desejado.
apresentado
𝑝
𝑖𝑒𝑞 = (1 + 𝑖) 𝑎−1
𝑖𝑒𝑞 = 𝑎
(1 + 𝑖)𝑝− 1
ou

16. • Taxas equivalentes são as taxas de juros fornecidas em
unidades de tempo diferentes.
• Quando estas são aplicadas a um mesmo principal
durante um mesmo prazo, produzem um mesmo
montante acumulado, no regime de juros compostos.
Período Comercial
1 mês = 30 dias em qualquer mês do ano
1 Ano = 360 dias

17. Lembre-se!
1 ano = 6 bimestres
1 ano = 4 trimestres
1 ano = 3 quadrimestres
1 ano = 2 semestres
1 biênio = 2 anos
1 triênio = 3 anos
Período Comercial

18. Série de Juros Compostos
Séries de juros compostos poderiam ter, também,
Parcelamento
Financiamento
em Juros
em Juros
como denominação
Compostos, ou ainda,
Compostos.
Cada parcela ou prestação são pequenos montantes
(M)
𝑀 = 𝐶. (1 + 𝑖) 𝑛
𝐶 =
𝑀
(1 + 𝑖) 𝑛

19. Cada parcela gera um capital, assim:
1
𝐶 =
𝑀1
(1+𝑖) 𝑛1 2
; 𝐶 =
𝑀2
(1+𝑖) 𝑛2 𝑗
; … ; 𝐶 =
𝑀𝑗
(1+𝑖) 𝑛𝑗

20. Logo:
Assim:
𝐶 = 𝐶1 + 𝐶2 + ⋯ + 𝐶𝑗
Então:
𝑀1 𝑀2 𝑀𝑗
𝐶 = + + ⋯ +
(1 + 𝑖) 𝑛1 (1 + 𝑖) 𝑛2 (1 + 𝑖) 𝑛𝑗
𝑗
𝑀𝑗
𝐶 = ෍
(1 + 𝑖) 𝑛𝑗
𝑗=1

21. Em uma situação em que trabalhamos com
pagamento de entrada (E), teremos:
𝐶 = 𝐴𝑉 − 𝐸
𝑗
𝑀𝑗
𝐶 = 𝐴𝑉 − 𝐸 = ෍
(1 + 𝑖. 𝑛𝑗 )
𝑗=1

22. Juros Simples: O juro simples é
calculado sempre sobre o valor do
capital inicial.
𝐽 = 𝐶. 𝑖. 𝑛
𝑀 = 𝐶(1 + 𝑖. 𝑛)
Série de Juros Simples: Cada
parcela ou prestação são pequenos
Montantes (M).
𝑗
𝑀𝑗
𝐶 = ෍
1 + 𝑖𝑛𝑗
𝑗=1
𝑗
𝑀𝑗
𝐴𝑉 − 𝐸 = ෍
1 + 𝑖𝑛𝑗
𝑗=1

23. Juros Compostos: O
Juro composto é calculado
sobre o montante relativo
ao período anterior.
𝑀 = 𝐶. (1 + 𝑖) 𝑛
Série de Juros
Compostos: Cada parcela
ou prestação são
pequenos Montantes (M).
𝑗
𝑀𝑗
𝐶 = ෍
1 + 𝑖 𝑛𝑗
𝑗=1
𝑗
𝑀𝑗
𝐶 = 𝐴𝑉 − 𝐸 = ෍
(1 + 𝑖. 𝑛𝑗)
𝑗=1