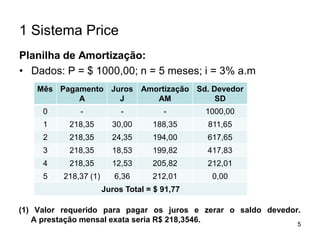
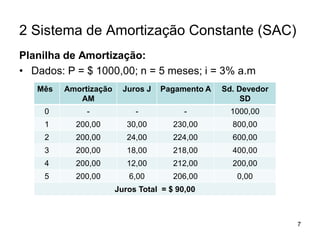
O documento resume os principais sistemas de amortização de empréstimos: Price e Amortização Constante. Explica que o sistema Price tem prestações constantes ao longo do tempo enquanto o sistema de Amortização Constante mantém uma parcela constante de amortização. Também discute carência, commitment fee e fornece exemplos numéricos para ilustrar os cálculos envolvidos.

1. Escola Politécnica da UFBA – Departamento de Engenharia Química
ENGD06 – Engenharia Econômica e Gestão - Herbert Oliveira – Aula 9
AULA 9 - Sistemas de Amortização de
Empréstimos
Salvador
2017

2. 2
Tópicos Abordados
1. SISTEMA PRICE
2. SISTEMA DE AMORTIZAÇÃO CONSTANTE (SAC)
3. ANÁLISE COMPARATIVA PRICE X SAC
4. CARÊNCIA E COMMITMENT FEE

3. 3
1 Sistema Price
• Apresenta prestações constantes durante todo o
período de amortização (Série Uniforme).
• O valor da prestação (A) pode ser obtida a partir da
seguinte relação:
)%,(. niPAPA 
Trata-se portanto de um problema típico A dado P.

4. 4
1 Sistema Price
Observações importantes:
• Cada pagamento inclui uma parcela de juros e uma de
amortização do saldo devedor.
• À medida que o saldo devedor vai sendo amortizado, a
parcela de juros vai diminuindo e a de amortização vai
aumentando, mantendo-se o pagamento constante.
Pagamento Total
Pagamento ($)
Juros
Amortização
Prestações
n(última)

5. 5
1 Sistema Price
Planilha de Amortização:
• Dados: P = $ 1000,00; n = 5 meses; i = 3% a.m
Mês Pagamento
A
Juros
J
Amortização
AM
Sd. Devedor
SD
0 - - - 1000,00
1 218,35 30,00 188,35 811,65
2 218,35 24,35 194,00 617,65
3 218,35 18,53 199,82 417,83
4 218,35 12,53 205,82 212,01
5 218,37 (1) 6,36 212,01 0,00
Juros Total = $ 91,77
(1) Valor requerido para pagar os juros e zerar o saldo devedor.
A prestação mensal exata seria R$ 218,3546.

6. 6
2 Sistema de Amortização Constante (SAC)
• Mantém ao longo do período uma parcela constante de
amortização do saldo devedor, à qual são somados os
juros.
• Como o saldo devedor diminui com a amortização, os
juros e os pagamentos são decrescentes .
Pagamento ($)
Juros
Amortização
Prestações
n(última)

7. 7
2 Sistema de Amortização Constante (SAC)
Planilha de Amortização:
• Dados: P = $ 1000,00; n = 5 meses; i = 3% a.m
Mês Amortização
AM
Juros J Pagamento A Sd. Devedor
SD
0 - - - 1000,00
1 200,00 30,00 230,00 800,00
2 200,00 24,00 224,00 600,00
3 200,00 18,00 218,00 400,00
4 200,00 12,00 212,00 200,00
5 200,00 6,00 206,00 0,00
Juros Total = $ 90,00

8. 8
3 Análise Comparativa Price X SAC
• O pagamento Inicial no SAC é maior
• A amortização inicial no SAC é maior
• O total de juros pagos no SAC é menor
• A maioria dos grandes financiamentos utiliza o
sistema SAC, pela simplicidade dos cálculos
envolvidos.
• O sistema Price é restrito a financiamentos
habitacionais, por resultar em prestações iniciais
menores, o que exige menor renda familiar.
• Sistema misto - SAM (BNH): utilizava a média das
prestações dos 2 sistemas anteriores.

9. 9
4 Carência e Commitment Fee
• Prazo de Carência:
– Período concedido para que se inicie o pagamento das
amortizações.
– O empréstimo não é amortizado e somente são pagos os juros
sobre o principal.
– Alguns casos: não se paga nem os juros.
• Commitment Fee = Taxa de Reserva
– Comum em financiamentos onde o principal é liberado em
parcelas.
– Taxa de reserva sobre a parcela do financiamento ainda não
sacada.

10. 10
4 Carência e Commitment Fee
Exemplo de Aplicação:
• Seja um empréstimo de R$ 100.000,00, nas seguintes
condições:
– Prazo de carência:2 anos
– Prazo de pagamento (exceto carência): 5 anos (Sistema SAC)
– Taxa de Juros: 10% a.a.
– Commitment fee: 0,5% a.a.
– Liberação do empréstimo: 3 parcelas anuais de R$ 20.000,00,
R$ 50.000,00 e R$ 30.000,00, com início no ano 0.
Problema: montar a planilha do financiamento.

11. 11
4 Carência e Commitment Fee
Solução:
ANO 0 1 2 3 4 5 6 7
Liberada 20000 50000 30000 - - - - -
A liberar. 80000 30000 - - - - - -
Amortiz. - - - 20000 20000 20000 20000 20000
Sd Dev. 20000 70000 100000 80000 60000 40000 20000 -
Juros - 2000 7000 10000 8000 6000 4000 2000
Comm.
Fee
- 400 150 - - - - -
Pagto
Total
- 2400 7150 30000 28000 26000 24000 22000
Total de Juros+ Comm. Fee: R$ 39.550,00

12. 12
4 Carência e Commitment Fee
Atividade 1 em Grupo (Valor: 0,5)
• Seja um empréstimo de R$ 1.100.000,00, nas seguintes
condições:
– Prazo de carência 4 anos
– Prazo de pagamento (exceto carência): 6 anos (Sistema SAC)
– Taxa de Juros: 6 % a.a.
– Commitment fee: 0,5% a.a.
– Liberação do empréstimo: 5 parcelas anuais de R$ 400.000,00,
R$ 200.000,00, R$ 200.000,00, R$ 200.000,00 e R$ 100.000,00,
com início no ano 0.
Problema: montar a planilha do financiamento.

13. 13
4 Carência e Commitment Fee
Atividade 2 em Grupo (Valor: 0,5)
• Seja um empréstimo de R$ 1.100.000,00, nas seguintes
condições:
– Prazo de carência 4 anos
– Prazo de pagamento (exceto carência): 6 anos (Sistema Price)
– Taxa de Juros: 6 % a.a.
– Commitment fee: 0,5% a.a.
– Liberação do empréstimo: 5 parcelas anuais de R$ 400.000,00,
R$ 200.000,00, R$ 200.000,00, R$ 200.000,00 e R$ 100.000,00,
com início no ano 0.
Problema: montar a planilha do financiamento.