1) O documento apresenta exercícios de matemática envolvendo equações do 2o grau, sistemas de equações, geometria plana e cônicas. 2) São propostos problemas para determinar coordenadas de pontos, comprimentos de segmentos, equações de retas e circunferências, e pertencimento de pontos a curvas. 3) São solicitados cálculos e identificações envolvendo elipses, hipérboles e circunferências.

1. ”± ‡•–‹„—Žƒ” ‘’—Žƒ” †ƒ
‹„—Žƒ” ƒ ‰‡Šƒ”‹ƒ
Multiplicando ambos os membros por q, fica:
9 + 9q2 – 30q = 0
Dividindo por 3 e ordenando, fica:
3q2 – 10q + 3 = 0, que é uma equação do segundo grau. PENGE 1
Resolvendo a equação do segundo grau acima
encontraremos q = 3 ou q = 1/3.
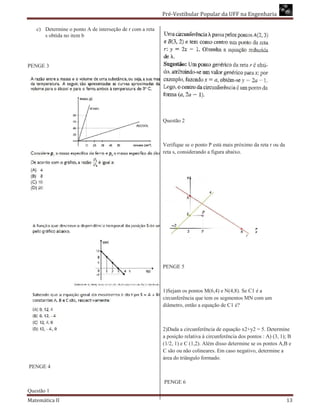
1 .Conhecendo-se o baricentro B(3,5), do triângulo XYZ
se
Como é dito que a PG é decrescente, devemos conside
considerar onde X(2,5), Y(-4,6), responda:
4,6),
apenas o valor a) Quais as coordenadas do vértice Z do triângulo
)
q = 1/3, já que para q = 3, a PG seria crescente. XYZ?
Portanto, a PG é:
9/q, 9, 9q, ou substituindo o valor de q vem: 27, 9 3.
9, b) Qual o comprimento do segmento BZ?
)
O problema pede a soma dos quadrados, logo:
a2 + b2 + c2 = 272 + 92 + 32 = 729 + 81 + 9 = 819 2. Seja a reta y = -2x, determine:
2x,
6.2 - Sabe-se que S = 9 + 99 + 999 + 9999 + ... + 999...9
se a) As coordenadas do ponto P que está no segundo
onde a última parcela contém n algarismos. Nestas quadrante, sobre a reta r e cuja distância ao ponto
condições, o valor de 10n+1 - 9(S + n) é: (0,-1) é ¥10 unidades;
10
A)1 b) As coordenadas do ponto Q, sobre a reta r, que esestá
*B) 10 mais próximo do ponto (0,(0,-1).
C) 100
D) -1
E) -10 PENGE 2
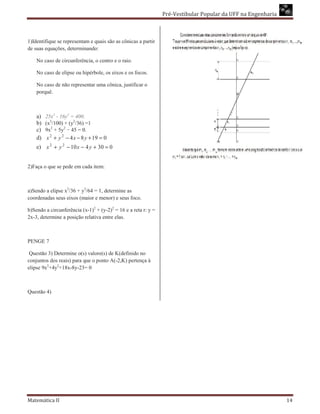
Solução: 1-Sendo o ponto P(r - 12, 4r - 6) pertencente a bissetriz dos
quadrantes ímpares e P’(s-12, 4s
12, 4s-13) pertencente a bissetriz
Observe que podemos escrever a soma S como:
rve dos quadrantes ímpares, determine:
S = (10 – 1) + (100 – 1) + (1000 – 1) + (10000 – 1) + ... +
(10n – 1)
a) O valor da distância entre P e P’.
S = (10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + ... + (10n –
1)
b) Qual dos pontos está mais próximo da origem.
ntos
Como existem n parcelas, observe que o número ( 1) é
(–
somado n vezes, 2. Considere o gráfico:
resultando em n(-1) = - n.
Logo, poderemos escrever:
S = (10 + 102 + 103 + 104 + ... + 10n ) – n
Vamos calcular a soma Sn = 10 + 102 + 103 + 104 + ... + 10n
, que é uma PG de primeiro termo a1 = 10, razão q = 10 e
último termo an = 10n . Teremos:
Sn = (an.q – a1) / (q –1) = (10n . 10 – 10) / (10 – 1) = (10n+1 –
10) / 9
Substituindo em S, vem:
S = [(10n+1 – 10) / 9] – n
Deseja-se calcular o valor de 10n+1 - 9(S + n)
Temos que S + n = [(10n+1 – 10) / 9] – n + n = (10n+1 – 10) /
9 a) Obtenha uma equação da reta r
Substituindo o valor de S + n encontrado acima, fica:
10n+1 – 9(S + n) = 10n+1 – 9(10n+1 – 10) / 9 = 10n+1 – (10n+1 – b) Obtenha uma equação da reta s que passa por P e é
10) = 10 perpendicular a r.
ƒ–‡ž–‹…ƒ