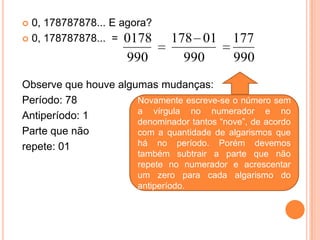
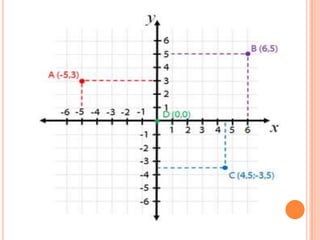
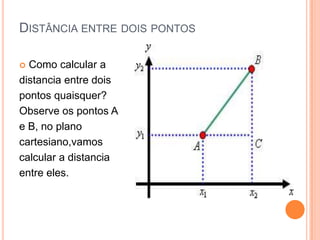
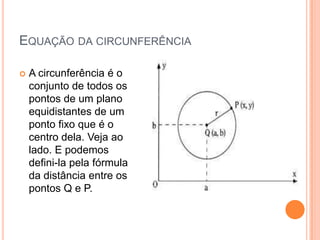
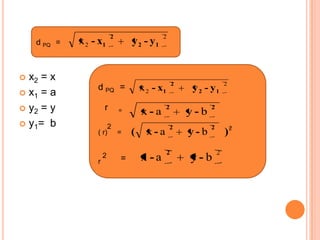
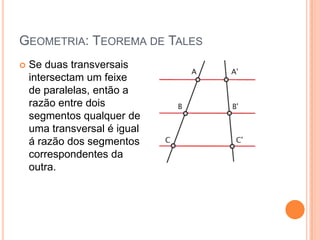
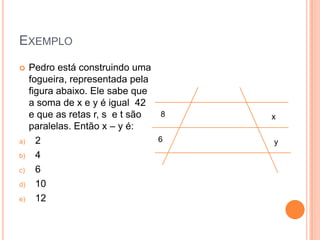
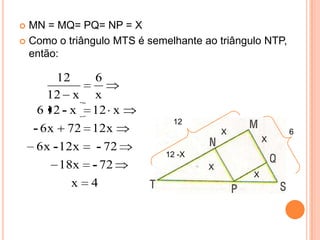
O documento aborda conceitos fundamentais de conjuntos numéricos, incluindo naturais, inteiros, racionais e irracionais, além de suas propriedades e representações. Também discute coordenadas cartesianas e fórmulas relacionadas, como a distância entre pontos e equação de circunferências. Por fim, menciona teoremas de geometria como o Teorema de Tales e a semelhança de triângulos, proporcionando uma rica revisão de matemática.

1. REVISÃO PARA A PROVA
Cristina Alves de S. Cardoso

2. CONJUNTOS NUMÉRICOS
 Um dos principais objetos de que se ocupa a
Matemática são os números e as figuras
geométricas. O objetivo desta revisão é recordar e
aprofundar o que você já estudou. Vejamos então
os conjuntos numéricos abaixo.

3. NÚMEROS NATURAIS (IN)
 O conjunto dos números naturais é representado
por:
IN 0,1,2,3,4,5,6,...
 Um subconjunto importante de IN é o conjunto IN*,
obtido excluindo o zero de IN.
IN * 1,2,3,4,5,6,...

4. NÚMEROS INTEIROS (Z)
 O conjunto dos números inteiros é representado por:
Z ..., 4, 3, 2, 1,0,1,2,3,4,...
 Destacamos os seguintes subconjuntos de Z:
 IN, pois IN é subconjunto de Z, ou seja, IN, está
 contido em Z.
 Z* = Z – {0} ou Z* = {..., -4, -3, -2, -1, 1, 2, 3, 4,...}
“Deus criou os números naturais. O resto é obra dos
homens.” Leopold Kronecker

5. NÚMEROS RACIONAIS (Q)
 Quando pensamos , por exemplo no cálculo de:
(-7) : (2) = ?, logo percebemos que esse resultado
não faz parte do conjunto dos números naturais e
tão pouco dos números inteiros. Daí a necessidade
de acrescentarmos as frações não aparentes, ou
seja aquela fração que indica um número inteiro.
 Assim por exemplo, são números racionais:
3 1 5
2, - , - 1, - , 0, , e 2.
2 2 3

6.  Desse modo escrevemos que todo número racional
é um número x, tal que x, é igual a sobre b, com a e
b pertencente ao inteiros e b diferente de zero.
Matematicamente, temos:
Q = { x/x = a , com a Z, b Z e b 0}.
b
Mas se os números racionais são números na forma
de fração como podemos dizer que -2 é um número
racional?
6 0
Simples, pois, 2 - assim como: 0
3 3

7. REPRESENTAÇÃO DECIMAL DOS NÚMEROS
RACIONAIS
 Dado um número racional
a, a representação
decimal desse número é b obtida dividindo-se a
por b , podendo resultar em:
 Decimais exatas, finitas:
1 4
0,25 e 0,8
4 5
 Decimais ou dízimas periódicas, infinitas:
2 177
0,6666... 0, 6 e 0,1787878.
.. 0, 178
3 990

8. FRAÇÃO GERATRIZ
 O decimal exato ou periódico que também pode
ser escrito na forma de fração, recebe o nome de
fração geratriz. Existem formas de se obter a fração
geratriz de uma dízima periódica: Veja os exemplos:
 I X = 0,222... .(10)
 II 10 X = 2,222... Resolvendo: II – I, temos:
 9X= 2
 X= 2
9

9.  I X = 0,17171717... .(10)
 II 10 X = 1,71717171... .(10)
 III 100 X = 17,171717..... Resolvendo: III – I, temos:
 99 X = 17
 X = 17
99
 Mas vejamos uma dica:
Escreve-se o número sem a
vírgula no numerador e no
 0,171717... = 017 17 denominador tantos “nove”,
de acordo com a quantidade
99 99 de algarismos que há no
Período = 17 período.
Antiperíodo = não há.

10.  0, 178787878... E agora?
 0, 178787878... = 0178 178 01 177
990 990 990
Observe que houve algumas mudanças:
Período: 78 Novamente escreve-se o número sem
a vírgula no numerador e no
Antiperíodo: 1
denominador tantos “nove”, de acordo
Parte que não com a quantidade de algarismos que
repete: 01 há no período. Porém devemos
também subtrair a parte que não
repete no numerador e acrescentar
um zero para cada algarismo do
antiperíodo.

11. VAMOS EXERCITAR?
 1) Determine a fração geratriz das dízimas periódicas:
a) 0,666...
b) 5,121212...
c) 2,1909090...
 2) Assinale a afirmação verdadeira.
a) 0,313131... é um número natural.
b) 5,47 é um número inteiro.
c) 3,1415926335... é um número real.
d) 5,171717... é um número racional.
...

12.  3) Em relação aos números racionais, todas as
alternativas são verdadeiras, exceto:
a) o conjunto dos naturais está contido no conjunto dos
números racionais.
b) o conjunto dos números inteiros pertence ao conjunto
dos números racionais.
c) 13 ; 0, 777...; 0; 4; ¾; -2; - 1/5; 0,3 são exemplos de
números racionais.
d) Todos os números racionais podem ser escritos na
forma de fração.

13. NÚMEROS IRRACIONAIS

14. COORDENADAS CARTESIANAS
 A notação (a, b) é usada para indicar o par
ordenado de números reais a e b, no qual a é a
primeira coordenada e o número b é a segunda
coordenada.
 O plano cartesiano é composto por um sistema de
eixos ortogonais, Ox e Oy, que tem a mesma origem
O. O eixo x é o das abscissas e y das ordenadas.
Dado um ponto P desse plano, dizemos que os
números a e b são as coordenadas cartesianas
desse
plano. Observe a seguir:

16. DISTÂNCIA ENTRE DOIS PONTOS
 Como calcular a
distancia entre dois
pontos quaisquer?
Observe os pontos A
e B, no plano
cartesiano,vamos
calcular a distancia
entre eles.

17.  A distância de A até B pode ser calculada através
da fórmula da distância abaixo.
2 2
d AB = x 2 - x1 y 2 - y1
Agora marque os pontos A( 1, -4) e B( -3, 2) no
plano cartesiano e depois calcule a distância entre
eles.

18. EQUAÇÃO DA CIRCUNFERÊNCIA
 A circunferência é o
conjunto de todos os
pontos de um plano
equidistantes de um
ponto fixo que é o
centro dela. Veja ao
lado. E podemos
defini-la pela fórmula
da distância entre os
pontos Q e P.

19. 2 2
d PQ = x 2 - x1 y 2 - y1
 x2 = x
2 2
d PQ = x 2 - x1 y 2 - y1
 x1 = a
 y2 = y r = x-a
2
y-b
2
 y1= b 2 2 2
( r) = ( x-a y-b )2
2 2
r
2 = x -a y-b

20.  Exemplo: Determine a equação da circunferência com
centro o(1, 4) e raio 2.
a=1 e b=4,r=2
 r2 = (x – a)2 + (y – b)2
 22 = (x – 1)2 + (y – 4)2
 4 = (x – 1)2 + (y – 4)2 logo a equação é:
 4 = (x – 1)2 + (y – 4)2 ou x² + y² - 2x - 8y +12 = 0 .
 Observação: Quando o centro da circunferência estiver
na origem, ou seja, O(0,0), a equação simplificada é
esta:
r² = x² + y²

21. GEOMETRIA: TEOREMA DE TALES
 Se duas transversais
intersectam um feixe
de paralelas, então a
razão entre dois
segmentos qualquer de
uma transversal é igual
á razão dos segmentos
correspondentes da
outra.

22. EXEMPLO
 Pedro está construindo uma
fogueira, representada pela
figura abaixo. Ele sabe que
a soma de x e y é igual 42
e que as retas r, s e t são 8 x
paralelas. Então x – y é:
a) 2 6 y
b) 4
c) 6
d) 10
e) 12

23. SEMELHANÇA DE TRIÂNGULOS
 Toda reta paralela a um lado de um triângulo que
intersecta os outros dois lados em pontos distintos
determina outro triângulo semelhante ao primeiro.
 Observe a atividade. (MACKENZIE - SP) Na figura
ao abaixo, MNPQ é um losango. Se MT = 12 e MS
= 6, quanto mede cada lado do losango?

24.  MN = MQ= PQ= NP = X
 Como o triângulo MTS é semelhante ao triângulo NTP,
então:
12 6
12 x x
6 12 - x 12 x
12
- 6 x 72 12x X 6
X
6 x - 12x - 72
12 -X
18x - 72 X
X
x 4

25. Só posso
MENSAGEM FINAL
ATÉ AQUI ME AJUDOU O
desejar a
SENHOR!!!!!!!!!!! vocês bons
Pense nisso. estudos e
ótimos
resultados. A
vida nos
apresenta
milhares de
pessoas. E
cada uma
delas vem
cumprir um
papel
em nossa
vida. Mas
cabe a nós o
papel
principal.Boa
prova a todos