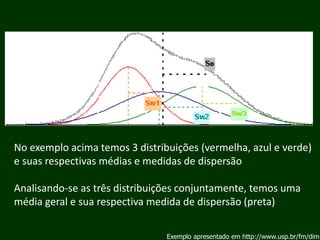
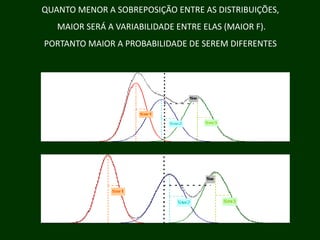
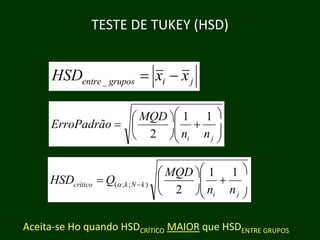
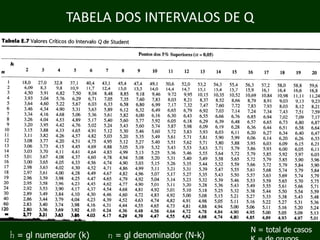
Este documento descreve a análise de variância (ANOVA), um teste estatístico que compara as médias de dois ou mais grupos. A ANOVA determina se as médias dos grupos são estatisticamente significativas ou se podem ter ocorrido por acaso. O teste compara a variância entre os grupos com a variância dentro dos grupos para calcular uma razão F que é comparada com valores críticos de F.

1. ANÁLISE
DE VARIÂNCIA
‐ ANOVA ‐

2. TRATA‐SE DE UM TESTE PARAMÉTRICO
Portanto:
• a amostragem deve ter sido aleatória
• as variáveis devem ter distribuição normal
• os grupos têm que ser independentes e
homocedásticos

3. A análise de variância permite que vários grupos
(
(distribuições) sejam comparados simultaneamente
ç ) j
p
Seu princípio é comparar a média e a dispersão dos
dados entre grupos de amostras com a dispersão
observada dentro dos mesmos
mesmos.
Variância total = variância dentro + variância entre os grupos

4. No exemplo acima temos 3 distribuições (vermelha, azul e verde)
p
ç
(
,
)
e suas respectivas médias e medidas de dispersão
Analisando‐se as três distribuições conjuntamente, temos uma
média geral e sua respectiva medida de dispersão (preta)
Exemplo apresentado em http://www.usp.br/fm/dim

5. QUANTO MENOR A SOBREPOSIÇÃO ENTRE AS DISTRIBUIÇÕES,
MAIOR SERÁ A VARIABILIDADE ENTRE ELAS (MAIOR F).
F)
PORTANTO MAIOR A PROBABILIDADE DE SEREM DIFERENTES

6. TABELA SINTESE
ANOVA UM FATOR
FONTE DE VARIÂNCIA
SOMA DOS QUADRADOS
GRAUS DE LIBERDADE
ENTRE GRUPOS
k-1
SQE
DENTRO DOS GRUPOS
N-k
SQD
TOTAL
N-1
SQT
∑ (X
∑ (X
∑ (X
FATOR: variável independente
GRUPO
ij
QUADRADOS MÉDIOS
)
− X T OTAL
− X GRUPO )
2
ij
− X TOTAL
)
2
MQE
SQE
Q
k −1
MQD
2
SQD
N − k
F
MQE
Q
MQD

7. RAZÃO F
INDICA A DIFERENÇA ENTRE OS GRUPOS EM FUNÇÃO DA
Ã
VARIAÇÃO DENTRO DE CADA GRUPO
RAZAO F = MQE / MQD
ONDE:
• o numerador representa a variação entre os grupos
p
ç
grupos
• o denominador representa a variação dentro desses g p

8. RAZÃO F
•
Ho: todas as médias são iguais
•
H1: nem todas as médias são iguais (ou seja, pelo menos um grupo de
amostras não é procedente d mesma população)
d
da
l
)
ACEITA SE
ACEITA‐SE HO QUANDO F CALCULADO É MENOR QUE F CRITICO
O VALOR DE F CRÍTICO PODE SER OBTIDO NA TABELA DE DISTRIBUIÇÃO
DE F OU A PARTIR DA FUNÇÃO INVF NO EXCEL
Ç
Assumimos k-1 graus de liberdade entre os grupos e N-k graus de
liberdade dentro dos grupos.

9. ANALISE DE VARIÂNCIA
FATOR ÚNICO
Trata‐se de uma análise de variância simples ( variável
p (1
independente) dos valores de dois ou mais grupos.
FATOR DUPLO
Aplicada quando os dados podem ser classificados com
base em duas dimensões diferentes ou duas variáveis
independentes.

10. COMPARAÇÕES DE MÉDIAS
A POSTERIORI OU POST HOC
Uma vez verificada a diferença entre os
grupos podem ser aplicados testes
d
li d
estatísticos para se identificar quais são
diferentes entre si.
Ho = os dois grupos são iguais
g p
g

11. COMPARAÇÕES DE MÉDIAS
A POSTERIORI OU POST HOC
Existem diferentes testes para este fim:
• Tukey HSD (Honestly Significantly Different
• Fisher’s LSD (Least Significant Difference method)
• Newman‐Keuls
l
• Dunnett comparação com um controle
Dunnett:

12. TESTE DE TUKEY (HSD)
HSDentre _ grupos = xi − x j
 MQD  1 1 
 +
ErroPadrão
E P dã = 

 2  ni n j 

HSDcrítico = Q(α ;k ; N − k )
íti
 MQD  1 1 
 +

 2  ni n j 

Aceita‐se Ho quando HSDCRÍTICO MAIOR que HSDENTRE GRUPOS

13. TABELA DOS INTERVALOS DE Q
h = gl numerador (k)
n = gl denominador (N-k)
N = total de casos
K = de grupos