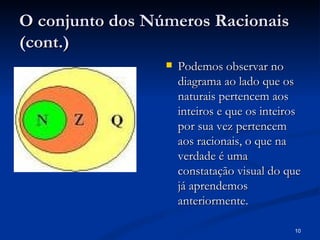
Este documento descreve o conjunto dos números racionais. Explica que os números racionais incluem frações como 1/1, 2/1, 3/1 e dízimas periódicas que podem ser expressas como frações. Também define subconjuntos dos números racionais como Q* (excluindo zero), Q+ (números positivos) e Q- (números negativos).

1. Matemática
Profª Beth Blanco
Números Racionais
1

2. O Conjunto dos Números Racionais
 Os números racionais
são todos aqueles que
podem ser colocados em
forma de fração, observe
que 1/1 , 2/1 , 3/1
também são frações, ou
seja, o conjunto dos
números racionais
“abraça” também os
naturais e os inteiros que
são seus subconjuntos.
2

3. Conjunto dos Números Racionais
 O conjunto dos números racionais é representado pela
letra Q e também é infinito.
 Fazem parte do Conjunto dos Números Racionais, os
naturais, os inteiros, a frações (razões entre dois
inteiros) e as dízimas periódicas(que podem ser
transformadas entre razões de dois inteiros).
 Observe uma representação dos números racionais:
Q = {..., -1, -1/2, 0 , 1/2, 1,...}
3

4. Conhecendo melhor os números
racionais.
 Você conhece as dízimas
periódicas? Como
dissemos anteriormente,
elas também pertencem
aos números racionais,se
conhece vamos
relembrar, se não, vamos
conhecê-las?
4

5. Dízimas periódicas, o que são?
 Toda fração é uma divisão de dois números
inteiros, por exemplo ½ é igual a 1 dividido por
2 o que resulta em 0,5. (dá uma conferidinha aí
na sua calculadora).
 Já as dízimas periódicas são divisões que
resultam infinitas e repetitivas, por exemplo 1/3
é um exemplo pois ao executar essa divisão
obtemos 0,3333333333333.... Infinitamente.
Pode conferir aí na sua calculadora!
5

6. Dizimas periódicas, o que são?
(cont)
 Mas se tivermos 1/3 já vamos dizer facilmente que
pertence aos racionais não é? Porém o que acontece é
que geralmente temos 0,333333....., mas nesse caso o
que fazer?
O primeiro passo é identificar o período, número que se
repete após a vírgula no caso acima é o 3.
O segundo passo é dividir o número que se repete, no
caso o 3, por tantos 9 quanto seja o número de termos
do período no caso temos apenas um número se
repetindo, então fica assim: 3/9 simplificando a
fração(dividindo por 3 o numerador e o denominador)
ficamos com 1/3.
6

7. Exemplo prático
 Transforme 0,32323232... Em uma razão de dois inteiros.
(tradução: transforme em uma fração)
Primeira pergunta: qual é o período? O que se repete infinitamente?
Resposta: 32
Segunda pergunta: quantos números tem esse período? Resposta: 2
números (3 e 2)
Agora estamos em condições de transformar 0,323232 em uma
fração basta colocar o período(número que se repete) no
numerador (parte de cima da fração) , no caso é 32 e no
denominador (parte de baixo da fração) colocamos tantos 9
quantos são os números do numerador( parte de cima da fração).
Assim, temos a resposta que é 32/99, pode conferir na sua
calculadora, sempre dá certo!
7

8. Conjunto dos números Racionais
(cont).
 O conjuntos dos números racionais tem seus
subconjuntos, vejamos:
 Q* (racionais, excluído o zero)
 Q+ (racionais positivos)
 Q- (racionais negativos)
8

9. Pausa para reflexão
 A partir deste momento
conseguimos compreender,
relacionar e representar os
números naturais, inteiros e
racionais, já sabemos que os
naturais pertencem aos
inteiros que por sua vez
pertencem aos racionais.e
portanto estamos prontos
para compreeender esta idéia
em diagrama.
9

10. O conjunto dos Números Racionais
(cont.)
 Podemos observar no
diagrama ao lado que os
naturais pertencem aos
inteiros e que os inteiros
por sua vez pertencem
aos racionais, o que na
verdade é uma
constatação visual do que
já aprendemos
anteriormente.
10