1) O documento discute seqüências e séries numéricas, definindo seqüências, apresentando exemplos e propriedades como convergência e monotonicidade. 2) Uma seqüência é uma função que associa números naturais a números reais. Exemplos incluem seqüências com termos definidos por fórmulas ou recorrência. 3) Uma seqüência converge se seu limite quando n tende ao infinito existe e é um número real finito. Caso contrário, diverge. Teoremas caracterizam convergência ou divergência.

1. Seqüências e Séries
Notas de Aula
4º Bimestre/2010
1º ano - Matemática
Cálculo Diferencial e Integral I
Profª Drª Gilcilene Sanchez de Paulo

2. Seq¨ˆncias e S´ries
ue
e
Para x ∈ R, podemos em geral, obter senx, ex , lnx, arctgx e valores de outras fun¸oes
c˜
transcendentes utilizando uma calculadora ou uma tabela.
Um problema fundamental consiste em determinar como as calculadoras calculam esses n´meros,
u
ou como se constr´i uma tabela.
o
As s´ries num´ricas infinitas (somas infinitas) podem ser usadas para obter valores funcionais
e
e
de uma certa fun¸ao f (x), ou seja, valores aproximados para f (c), c ∈ R.
c˜
Portanto, temos que interpretar essas “somas infinitas” e saber o seu significado preciso. Lidar
com o infinito sempre foi um problema dif´
ıcil; e os matem´ticos sabem disso h´ mais de dois
a
a
milˆnios. E para que n´s tenhamos uma id´ia das dificuldades que podem surgir, vamos logo dar
e
o
e
um exemplo simples e bastante esclarecedor. Considere a soma infinita,
S = 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + ···
Se escrevermos S = (1 − 1) + (1 − 1) + (1 − 1) + (1 − 1) + · · · , teremos S = 0. Mas podemos
tamb´m escrever S = 1 − (1 − 1) − (1 − 1) − (1 − 1) − (1 − 1) − · · · e agora conclu´
e
ımos que S = 1.
Ainda h´ uma terceira possibilidade, t˜o leg´
a
a
ıtima como as anteriores:
S = 1 − (1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + · · · ) = 1 − S ⇒ 2S = 1 ⇒ S = 1/2 .
Afinal, S = 0, S = 1 ou S = 1/2? Por que trˆs respostas diferentes? Claro que n˜o podemos
e
a
aceitar nenhuma delas em detrimento das outras.
Este exemplo aponta para a necessidade de se conceituar o que significa “soma infinita”. Como
veremos, essa conceitua¸˜o excluir´ a possibilidade de somas infinitas do tipo que acabamos de
ca
a
considerar. E para chegar a essa conceitua¸ao devemos primeiro estudar as chamadas “seq¨ˆncias
c˜
ue
num´ricas”.
e
1
Seq¨ˆncias num´ricas
ue
e
Defini¸˜o 1. Uma seq¨ˆncia de n´meros reais ´ uma fun¸˜o a : N → R que associa a cada n´mero
ca
ue
u
e
ca
u
natural n a um n´mero real a(n), indicado por an , o qual ´ chamado n−´simo termo da seq¨ˆncia.
u
e
e
ue
Figura 1: Representa¸ao gr´fica de uma seq¨ˆncia num´rica.
c˜
a
ue
e
Um exemplo concreto de seq¨ˆncia num´rica ´ dado pela seq¨ˆncia dos n´meros pares positivos
ue
e
e
ue
u
(2, 4, 6, 8, 10, · · · , 2n, · · · ), cujo termo geral da seq¨ˆncia ´ designado por an = 2n, n = 1, 2, 3, · · · .
ue
e
A seq¨ˆncia dos n´meros ´
ue
u
ımpares positivos tamb´m tem uma f´rmula simples para o termo geral,
e
o
a qual ´ dada por an = 2n + 1, com n = 0, 1, 2, 3, · · · ; ou an = 2n − 1 para n = 1, 2, 3, · · · .
e
Mas nem sempre o termo geral de uma seq¨ˆncia ´ dado por uma f´rmula, embora, evidenue
e
o
temente, sempre haja uma lei de forma¸ao bem definida que permite determinar o termo geral
c˜
√
´ esse o caso das aproxima¸˜es decimais por falta de 2, que formam a seq¨ˆncia
da seq¨ˆncia. E
ue
co
ue
infinita
a1 = 1, 4; a2 = 1, 41; a3 = 1, 414; a4 = 1, 4142; a5 = 1, 41421; a6 = 1, 414213; · · ·
1

3. Outro exemplo ´ a seq¨ˆncia dos n´meros primos,
e
ue
u
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, · · ·
Como se sabe, n˜o existe f´rmula para o termo geral da seq¨ˆncia dos n´meros primos, mas
a
o
ue
u
todos eles est˜o determinados e podem ser encontrados, por exemplo, pelo chamado “crivo de
a
Erat´stenes”.
o
A nota¸ao (an ) ´ muito usada para denotar uma seq¨ˆncia. Tamb´m se escreve (a1 , a2 , a3 , · · · ),
c˜
e
ue
e
ou (an )n∈N ,ou simplesmente an . Podemos tamb´m usar quaisquer outras letras, como (bn ), (cn ),
e
(xn ), (yn ), (zn ), etc. Alguns autores costumas escrever {an } em vez de (an ), mas preferimos
reservar essa nota¸ao entre chaves para o conjunto de valores da seq¨ˆncia. Essa distin¸˜o ´
c˜
ue
ca e
importante, pois uma seq¨ˆncia possui infinitos elementos, mesmo que seu conjunto de valores seja
ue
finito. Por exemplo, a seq¨ˆncia (+1, −1, +1, −1, +1, −1, +1, −1, · · · ), ´ infinita, com elemento
ue
e
(n−1)
gen´rico an = (−1)
e
; mas o seu conjunto de valores possui apenas dois elementos , +1 e -1, de
forma que, segundo convencionamos, {an } = {−1, +1}.
Exemplos
(1) Seq¨ˆncia de termo geral an = 2n . (2, 4, 8, 16, 32, · · · )
ue
(2) Seq¨ˆncia de termo geral an =
ue
n
.
n+1
1 2 3 4
, , , ,···
2 3 4 5
(1)
(2)
Figura 2: Representa¸ao gr´fica das seq¨ˆncias num´ricas (1) e (2).
c˜
a
ue
e
Observamos que quando n cresce infinitamente, os termos an da seq¨ˆncia (1) tamb´m crescem
ue
e
infinitamente. Ao passo que os termos an da seq¨ˆncia (2) acumulam-se pr´ximos ao n´mero 1.
ue
o
u
n
(3) Seja an =
tk , t = 0 e t = 1. Calcule o termo geral da seq¨ˆncia (an ).
ue
k=0
Solu¸˜o: an = 1+t+t2 +· · ·+tn . Multiplicando pelo fator t obtemos, tan = t+t2 +t3 · · ·+tn+1 .
ca
Assim,
1 − tn+1
an − tan = 1 − tn+1 ⇒ (1 − t)an = 1 − tn+1 ⇒ an =
.
1−t
Note que an ´ a soma dos (n + 1) primeiros termos da P.G. 1, t, t2 , · · · , tn , · · · .
e
Para algumas seq¨ˆncias damos o primeiro termo a1 e uma regra que permite determinar qualue
quer termo ak+1 a partir do termo precedente, para k ≥ 1. Isto ´ o que constitui uma defini¸˜o
e
ca
por recorrˆncia e a seq¨ˆncia ´ dita definida por recorrˆncia.
e
ue
e
e
2

4. (4) Ache os quatro primeiros termos e o n−´simo termo da seq¨ˆncia definida por a1 = 3 e
e
ue
ak+1 = 2ak para k ≥ 1.
a1 = 3 = 2 0 · 3
a2 = 2a1 = 2 · 3 = 6 = 21 · 3
a3 = 2a2 = 2.6 = 12 = 22 · 3
a4 = 2a3 = 2.12 = 24 = 23 · 3
Isto sugere que an = 2n−1 · 3.
´
E poss´ provar por indu¸ao finita que a suposi¸ao ´ correta. Prove!
ıvel
c˜
c˜ e
1.1
Seq¨ˆncias convergentes e divergentes
ue
Algumas seq¨ˆncias apresentam uma propriedade de que quando n cresce arbitrariamente, an
ue
se aproxima de um n´mero real L, ou seja, a diferen¸a |an − L| ´ t˜o pequena quanto se deseja,
u
c
e a
desde que n seja suficientemente grande.
Defini¸˜o 2. Seja (an ) uma seq¨ˆncia num´rica e L um n´mero real. Dizemos que
ca
ue
e
u
(i) lim an = L ⇐⇒ ∀ ε > 0;
n→+∞
∃ N ∈ N : ∀ n > N =⇒ |an − L| < ε.
(ii) lim an = +∞ ⇐⇒ ∀ M > 0;
∃ N ∈ N : ∀ n > N =⇒ an > M .
(iii) lim an = −∞ ⇐⇒ ∀ M > 0;
∃ N ∈ N : ∀ n > N =⇒ an < −M .
n→+∞
n→+∞
Figura 3: Representa¸ao gr´fica de uma seq¨ˆncia an que se aproxima de um n´mero real L.
c˜
a
ue
u
Na figura 3, exibimos uma seq¨ˆncia (an ) tal que lim an = L.
ue
n→+∞
Defini¸˜o 3. Se existe um n´mero real (finito) L tal que lim an = L a seq¨ˆncia (an ) ´ dita
ca
u
ue
e
n→+∞
convergente. Caso contr´rio, a seq¨ˆncia ´ dita divergente.
a
ue
e
3

5. Exemplo
(5) Utilize a defini¸ao para provar que a seq¨ˆncia
c˜
ue
n−1
1 2 3
, · · · , cujo termo geral
0, , , , · · · ,
2 3 4
n
n−1
´ an =
e
, tem limite L = 1.
n
Solu¸˜o:
ca
Exerc´
ıcio: (1) Prove utilizando a defini¸ao de limite que a seq¨ˆncia (an ) =
c˜
ue
n
n + 12
converge
para o n´mero 1.
u
Solu¸˜o:
ca
Alguns Teoremas para convergˆncia de seq¨ˆncias
e
ue
Teorema 1. a) lim rn = 0, se |r| < 1
n→+∞
b) lim rn n˜o existe se |r| > 1
a
n→+∞
Teorema 2 (Teorema do Confronto). Sejam (an ), (bn ) e (cn ) seq¨ˆncias tais que lim an = L =
ue
n→+∞
lim cn . Se existe n1 ∈ N tal que an ≤ cn ≤ bn , para todo n > n1 , ent˜o lim bn = L.
a
n→+∞
n→+∞
Observa¸˜o: Se suprimirmos de uma seq¨ˆncia an um n´mero finito de seus termos, isso n˜o
ca
ue
u
a
altera em nada o car´ter da seq¨ˆncia com n no infinito. Assim, se a seq¨ˆncia original converge
a
ue
ue
para L, ou diverge, a nova seq¨ˆncia convergir´ para L ou divergir´, respectivamente.
ue
a
a
Teorema 3. Seja (an ) uma seq¨ˆncia. Se lim |an | = 0, ent˜o lim an = 0.
ue
a
n→+∞
n→+∞
4

6. Exerc´
ıcio: (2) Utilizando a Defini¸˜o 3, os Teoremas 1, 2 e 3, verifique se s˜o convergentes ou
ca
a
divergentes as seguintes seq¨ˆncias:
ue
a)
n2 + 2n − 1
2n2 + 5
(−1)n+1
d) an =
n
i)
1.2
ln n
n
n
b) an =
tk , 0 < t < 1,
c) an =
k=0
n
e) (1, 01)
j) (101−n )
f)
5n
e2n
g)
cos2 n
3n
−
2
3
n
h) (n · sen(π/2n))
√
l) ( n n)
k) an = (−1)n
Seq¨ˆncias Mon´tonas
ue
o
Defini¸˜o 4. Dizemos que uma seq¨ˆncia (an ) ´ mon´tona n˜o-decrescente (ou crescente) se, para
ca
ue
e
o
a
todos os naturais m, n tais que m < n implicar am ≤ an (ou am < an ). Se m < n implicar
am ≥ an (ou am > an ) dizemos que a seq¨ˆncia (an ) ´ mon´tona n˜o-crescente (ou decrescente).
ue
e
o
a
Defini¸˜o 5. Uma seq¨ˆncia (an ) ´ limitada se existe um n´mero real positivo K tal que |an | ≤ K,
ca
ue
e
u
∀ n ∈ N.
Teorema 4. Se (an ) ´ uma seq¨ˆncia convergente ent˜o (an ) ´ limitada.
e
ue
a
e
Pergunta: Toda seq¨ˆncia limitada ´ convergente?
ue
e
Solu¸˜o: N˜o. Considere a seq¨ˆncia an = (−1)n . Evidentemente, a seq¨ˆncia ´ limitada, |an | ≤ 1,
ca
a
ue
ue
e
∀ n ∈ N. Entretanto, os valores desta seq¨ˆncia alternam de −1 para 1 indefinidamente, e porue
tanto ela n˜o ´ convergente.
a e
Teorema 5. Se (an ) ´ uma seq¨ˆncia mon´tona e limitada ent˜o (an ) ´ convergente.
e
ue
o
a
e
Teorema 6. a) Se (an ) ´ uma seq¨ˆncia mon´tona cresecente (ou n˜o-decrescente) e ilimitada
e
ue
o
a
superiormente ent˜o lim an = +∞.
a
n→+∞
b) Se (an ) ´ uma seq¨ˆncia mon´tona decresecente (ou n˜o-crescente) e ilimitada
e
ue
o
a
inferiormente ent˜o lim an = −∞.
a
n→+∞
Exemplo
(6) A seq¨ˆncia
ue
5n
3n n!
´ convergente.
e
Solu¸˜o:
ca
5

7. Exerc´
ıcio: (3) Verifique se s˜o convergentes ou divergentes as seguintes seq¨ˆncias:
a
ue
a) an =
n−1
n2n
b) an = (−1)n
2n
3n + 1
6

8. Lista 11: Seqüências
A) Exercícios do Guidorizzi – Vol. 4 – Páginas 6 - 10:
Exercícios 1.1
(1)
(2) a-b-c-d-l-m-n-o-q-s
(3)
(4) a-b
B)
an  8n  1
 4n 4  1 
 2 
 2n  1 
 1  n 


 1   
 n  


Respostas dos exercícios de número ímpar do bloco B)
(5)
(9)
(12)

9. 2
S´ries num´ricas
e
e
∞
an = a1 +a2 +a3 +· · ·+an +· · · ´
e
Defini¸˜o 6. Seja (an ) uma seq¨ˆncia infinita. A soma infinita
ca
ue
n=1
chamada s´rie num´rica infinita de termo geral an . Se somarmos apenas os n primeiros termos
e
e
n
ak = a1 + a2 + a3 + · · · + an .
desta s´rie, teremos o que chamamos de soma parcial Sn =
e
k=1
Exemplos
∞
(7) A seq¨ˆncia dos n´meros pares fornece a s´rie 2 + 4 + 6 + · · · =
ue
u
e
2n de termo geral an = 2n.
n=1
(8) A seq¨ˆncia num´rica (1, 2, 6, 24, 120, 720, · · · ) fornece a s´rie 1 + 2 + 6 + 24 + 120 + 720 + · · · =
ue
e
e
∞
n! de termo geral an = n!.
n=1
(9) A seq¨ˆncia num´rica
ue
e
1 1
1
1, , , · · · , , · · ·
2 3
n
fornece a s´rie 1 +
e
1
1
+ + ··· =
2
3
∞
1
, de
n=1 n
1
, conhecida como s´rie harmˆnica.
e
o
n
1 1 1 1 1
1
1 1 1
(10) A seq¨ˆncia num´rica
ue
e
, , , , ,··· ,
, · · · fornece a s´rie + + +· · · =
e
2 6 12 20 30
n(n + 1)
2 6 12
∞
1
1
, de termo geral an =
, conhecida como s´rie telesc´pica.
e
o
n(n + 1)
n=1 n(n + 1)
termo geral an =
∞
Defini¸˜o 7. Dizemos que um n´mero real S ´ a soma da s´rie
ca
u
e
e
∞
an , ou que a s´rie
e
n=1
an
n=1
converge para S quando lim Sn = S ( o limite da seq¨ˆncia das somas parciais (S1 , S2 , S3 , · · · )
ue
n→+∞
∞
´ S). Neste caso, escrevemos S =
e
∞
an . Quando lim Sn n˜o existe, dizemos que a s´rie
a
e
n→+∞
n=1
an
n=1
diverge.
Exemplos
(11) A s´rie
e
∞
(−1)n+1 = 1 − 1 + 1 − 1 + · · · diverge. Trata-se da s´rie que nos motivou a
e
n=1
conceituar soma infinita.
Solu¸˜o:
ca
• Seq¨ˆncia das somas parciais:
ue
S1 = a1 =,
S2 = a1 + a2 =,
S3 = a1 + a2 + a3 =,
S4 = a1 + a2 + a3 + a4 =,
.
.
.
Sn = a1 + a2 + · · · + an =.
7

10. • Limite da seq¨ˆncia (Sn ): lim Sn =
ue
n→∞
∞
n = 1 + 2 + 3 + 4 + · · · + n + · · · diverge.
(12) A s´rie
e
n=1
Solu¸˜o:
ca
• Seq¨ˆncia das somas parciais:
ue
• Limite da seq¨ˆncia (Sn ): lim Sn =
ue
n→∞
∞
(13) A s´rie
e
1 1 1
1
1
= + + + · · · + n + · · · converge.
n
2 4 8
2
n=1 2
Solu¸˜o:
ca
• Seq¨ˆncia das somas parciais:
ue
• Limite da seq¨ˆncia (Sn ): lim Sn =
ue
n→∞
(11)
(12)
(13)
Figura 4: Representa¸ao da seq¨ˆncia (Sn ) dos exemplos (11), (12) e (13).
c˜
ue
Exerc´
ıcio
(4) Determine a s´rie infinita que tem a seguinte seq¨ˆncia de somas parciais. Al´m disso, verifique
e
ue
e
se a s´rie ´ convergente ou divergente.
e e
4n
2n
n2
b) Sn =
c) Sn =
d) (Sn = 2n )
a) Sn =
n+1
3n + 1
n+1
8

11. 2.1
S´ries Geom´tricas
e
e
∞
Uma s´rie geom´trica ´ da forma a + ar + ar2 + ar3 + · · · + arn−1 + · · · =
e
e
e
arn−1 , com a = 0.
n=1
A n−´sima soma parcial da s´rie geom´trica ´ Sn =
e
e
e
e
De fato,
a(1 − rn )
, r = 1.
1−r
a
.
n→∞
n→∞
1−r
n
• Se |r| > 1 =⇒ lim r n˜o exite, e assim, lim Sn n˜o existe.
a
a
n→∞
n→∞
• Se r = 1, ent˜o Sn = na e portanto, lim Sn = lim na n˜o existe.
a
a
n→∞
n→∞
• Se r = −1, ent˜o Sn oscila e portanto, lim Sn n˜o existe.
a
a
• Se |r| < 1 =⇒ lim rn = 0, e assim, lim Sn =
n→∞
Conclus˜o
a
A s´rie geom´trica converge se |r| < 1 e a sua soma ´ S =
e
e
e
A s´rie geom´trica diverge se |r| ≥ 1.
e
e
a
.
1−r
Exerc´
ıcios
(5) Determine
1
a) 1 + +
2
∞
d)
1
se a s´rie ´ convergente ou divergente, se convergente encontre a soma.
e e
1 1
3 9 27 81
2 4
8
16
+ + ···
b) 1 + + +
+
···
c) −1 + − +
−
···
4 8
2 4
8
16
3 9 27 81
e) 0, 3 + 0, 03 + 0, 003 + 0, 0003 + · · ·
n=1
(6) Expresse a d´
ızima peri´dica 2, 358585858..... como raz˜o de dois inteiros.
o
a
2.2
S´rie Harmˆnica
e
o
∞
A s´rie
e
1
´ conhecida como s´rie harmˆnica.
e
e
o
n=1 n
O Teorema enunciado a seguir ser´ utilizado para provar a divergˆncia da s´rie harmˆnica.
a
e
e
o
∞
an ´ convergente ent˜o, dado ε > 0, ∃ N ∈ N tal que |Sm − Sn | < ε para
e
a
Teorema 7. Se a s´rie
e
n=1
todo m, n > N .
9

12. A s´rie harmˆnica ´ divergente.
e
o
e
De fato,
2.3
S´rie Telesc´pica
e
o
∞
A s´rie
e
1
´ conhecida como s´rie telesc´pica.
e
e
o
n=1 n(n + 1)
A s´rie telesc´pica ´ convergente.
e
o
e
De fato,
2.4
Propriedades das s´ries
e
∞
(P1) Se
∞
n=1
∞
E vale,
∞
(P2) Se
∞
an .
n=1
∞
an e
n=1
∞
n=1
n=1
∞
(an ± bn ) =
n=1
∞
an ±
n=1
∞
bn .
n=1
∞
an converge e
n=1
∞
(P4) Se
∞
∞
n=1
∞
bn divergem, ent˜o
a
n=1
(an ± bn ) diverge.
bn diverge, ent˜o
a
n=1
an e
n=1
(an ± bn ) tamb´m converge.
e
bn convergem, ent˜o
a
E vale,
(P3) Se
n=1
can = c
n=1
∞
can tamb´m converge, ∀ c ∈ R.
e
an converge, ent˜o
a
(an ± bn ) pode divergir ou convergir.
n=1
No momento oportuno, veremos exemplos para a (P4).
10

13. Exemplos
(14) Justifique, utilizando as propriedades acima, se a s´rie a seguir ´ convergente ou divergente.
e
e
∞
∞ 5
∞
1
1
1
c)
a)
b)
−
+ 2n
2n
2n 3n
3n
n=1
n=1
n=1
Para muitas s´ries ´ d´
e
e ıficil ou praticamente imposs´
ıvel encontrar uma f´rmula simples para
o
Sn . Em tais casos, s˜o usados alguns testes que n˜o nos fornecem a soma S da s´rie; dizem-nos
a
a
e
apenas se a soma existe. Isto ´ suficiente na maioria das aplica¸oes porque, sabendo que a soma
e
c˜
existe, podemos aproximar o seu valor com um grau arbitr´rio de precis˜o, bastanto somar um
a
a
n´mero suficiente de termos da s´rie.
u
e
2.5
S´ries de termos positivos
e
∞
an ´ uma s´rie de termos positivos e se existe K > 0 tal que Sn ≤ K, ∀ n ∈ N,
e
e
Teorema 8. Se
n=1
∞
ent˜o a s´rie
a
e
an converge.
n=1
Em uma s´rie de termos positivos, ´ evidente, que (Sn ) ´ mon´tona n˜o-decresente S1 ≤ S2 ≤
e
e
e
o
a
S3 ≤ · · · ≤ Sn ≤ · · · , pois a1 ≤ a1 + a2 ≤ a1 + a2 + a3 ≤ · · · ≤ a1 + a2 + · · · + an ≤ · · · . Portanto,
∞
basta verificar se a seq¨ˆncia (Sn ) ´ limitada para concluir se a s´rie
ue
e
e
an ´ convergente ou
e
n=1
divergente, segundo os Teoremas 5 e 6, respectivamente.
Exemplo
∞
(15) Verifique se a s´rie
e
2.6
n−1
converge.
n
n=1 n2
Teste da Divergˆncia
e
∞
Teorema 9 (Teorema da divergˆncia). Se lim an = 0, ent˜o a s´rie
e
a
e
n→∞
an diverge.
n=1
De fato,
CUIDADO: lim an = 0 n˜o garante a convergˆncia da s´rie. (Ver s´rie harmˆnica).
a
e
e
e
o
n→∞
Exemplo
(16) Prove que as s´ries s˜o divergentes:
e
a
n2 + 1
n2
n=1
∞
a)
∞
b)
n=1
2(−1)n+1
c)
1 2 3
n
+ + +· · ·+
+· · ·
3 5 7
2n + 1
11
∞
d)
ln
n=1
n
.
n+1

14. ∞
Exemplos para a (P4):
e)
n=1
2.7
1
+1
n
∞
f)
n=1
1
1
−
n n+1
Teste da Integral
∞
Teorema 10. Sejam
an uma s´rie de termos positivos e f uma fun¸ao cont´
e
c˜
ınua, tal que
n=1
f (n) = an , ∀ n ∈ N. Ent˜o,
a
∞
∞
an converge ⇐⇒
n=1
f (x) dx converge.
1
Exemplo
(17) Determine se a s´rie dada ´ convergente ou divergente:
e
e
∞
∞
a)
2.8
1
n=1 n
∞
1
2
n=1 n
b)
c)
1
√
n
n=1
∞
d)
e)
n=1
1
√
n=1 n ln n
S´rie-p
e
∞
Uma s´rie do tipo
e
1
´ denominada S´rie-p.
e
e
p
n=1 n
A s´rie-p converge se p > 1. Caso contr´rio, se p ≤ 1, a s´rie-p diverge.
e
a
e
De fato,
2.9
Teste da compara¸˜o
ca
∞
Teorema 11. Sejam
∞
∞
an e
n=1
bn s´ries de termos positivos.
e
n=1
∞
bn converge e an ≤ bn , ∀ n > N ∈ N, ent˜o
a
a) Se
an converge.
n=1
∞
n=1
∞
bn diverge e bn ≤ an , ∀ n > N ∈ N, ent˜o
a
b) Se
n=1
an diverge.
n=1
12
∞
∞
e−n
f)
n=1
ne−n

15. Exemplo
(18) Determine se a s´rie dada ´ convergente ou divergente:
e
e
∞
√
5n n
c)
.
2
n=1 13n − n − 10
∞
sen(3n)
a)
2
n=1 n + 1
∞
17n
b)
3
n=1 5n − 1
∞
Para utilizarmos um Teste da Compara¸˜o devemos primeiro escolher uma s´rie
ca
e
bn aden=1
quada para ent˜o provar que an ≤ bn ou bn ≤ an para todo inteiro n maior do que algum inteiro
a
positivo N . Esta prova pode ser dif´ se an ´ uma express˜o complicada. O teorema seguinte ´
ıcil
e
a
e
∞
um teste de compara¸˜o mais f´cil de aplicar porque escolhida
ca
a
bn , basta calcular o limite do
n=1
quociente an /bn quando n → ∞.
∞
∞
Teorema 12. Se
an e
n=1
an
= c > 0. Ent˜o, ou
a
n→∞ bn
bn s˜o s´ries de termos positivos e se lim
a e
n=1
ambas as s´ries convergem, ou ambas divergem.
e
∞
Para obter uma s´rie
e
bn conveniente para ser usada na forma limite do teste da compara¸ao
c˜
n=1
no caso em que an ´ um quociente,um bom processo consiste em reter apenas os termos do numee
rador e do denominador que tˆm o maior efeito sobre a magnitude. Podemos tamb´m substituir
e
e
∞
qualquer fator constante c por 1, pois
∞
bn e
n=1
an
cbn s˜o ambas convergentes ou divergentes.
a
n=1
termos de maior magnitude escolha de bn
3n + 1
+ n2 − 2
3n
3
= 2
3
4n
4n
4n3
1
n2
√
3
√
3
n2 + 4
6n2 − n − 1
n2
1
= 4/3
2
6n
6n
1
n4/3
Tabela 1: Ilustra¸ao para escolha de bn .
c˜
Exemplo
(19) Determine se as s´ries seguintes convergem ou divergem:
e
∞
a)
2.10
1
n
n=1 2 + 5
∞
√
b)
n=1
3
n−1
∞
c)
1
√
3
n2 + 1
n=1
3n2 + 5n
n
2
n=1 2 (n + 1)
∞
d)
S´ries Alternadas
e
Uma s´rie infinita ´ denominada s´rie alternada quando seus termos s˜o alternadamente
e
e
e
a
∞
positivos e negativos. Isto ´,
e
∞
(−1)n−1 an = a1 − a2 + a3 − a4 + · · · + (−1)n−1 an + · · · ou
n=1
n
(−1) an = −a1 + a2 − a3 + a4 − · · · + (−1)n an + · · · .
n=1
13

16. Teorema 13 (Teste de Leibniz). Em uma s´rie alternada,
e
Se an ≥ an+1 e lim an = 0, ent˜o a s´rie ´ convergente.
a
e e
n→∞
Conseq¨ˆncia: Em uma s´rie alternada, se an ≥ an+1 e lim an = c > 0, ent˜o a s´rie ´
ue
e
a
e e
n→∞
divergente.
Exemplo
(20) Determine se as seguintes s´ries alternadas convergem ou divergem:
e
∞
a)
(−1)n−1
n=1
2.11
∞
2n
4n2 − 3
b)
(−1)n−1
n=1
2n
4n − 3
∞
c)
(−1)n
n=1
n+2
n(n + 1)
(−1)n
n
n=1
∞
d)
Convergˆncia Absoluta e Convergˆncia Condicional
e
e
∞
∞
Defini¸˜o 8. Uma s´rie infinita
ca
e
n=1
vergente
Exemplo
∞
(21) Verifique se a s´rie
e
(−1)n
n=1
n=1
1
´ absolutamente convergente.
e
n2
∞
Teorema 14. Se
|an | ´ cone
an ´ dita absolutamente convergente se a s´rie
e
e
∞
an ´ absolutamente convergente ent˜o
e
a
n=1
an ´ convergente.
e
n=1
Exemplo
∞
(22) Verifique se a s´rie
e
sen(n)
converge.
n2
n=1
∞
Defini¸˜o 9. Uma s´rie infinita
ca
e
an ´ dita condicionalmente convergente se a s´rie ´ convergente,
e
e e
n=1
∞
|an | ´ divergente.
e
mas
n=1
Exemplo
∞
(23) Verifique que a s´rie alternada
e
(−1)n−1
n=1
1)
´ condicionalmente convergente.
e
n
Exerc´
ıcios
(7) Determine se a s´rie ´ absolutamente convergente, condicionalmente convergente ou divergente.
e e
∞
∞
∞ cos(nπ/6))
∞
1)
2( 1/n))
1)
a)
(−1)n−1 √
c)
d)
(−1)n
b)
(−1)n−1
ln(n + 1)
n2
n!
2n + 1
n=1
n=1
n=1
n=1
14

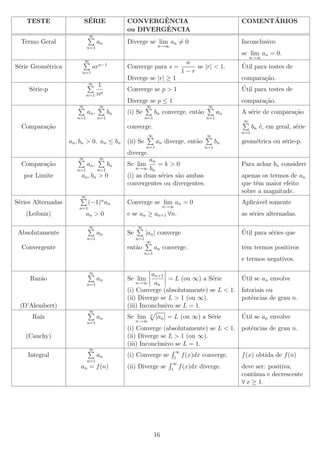
17. 2.12
Teste da Raz˜o
a
∞
Teorema 15 (Crit´rio D’Alembert). Seja
e
an uma s´rie de termos n˜o nulos.
e
a
n=1
an+1
= L.
an
(a) Se L < 1 ent˜o a s´rie ´ absolutamente convergente.
a
e e
(b) Se L > 1 ou L = +∞ ent˜o a s´rie diverge.
a
e
(c) Se L = 1 nada se pode concluir.
Seja lim
n→∞
Exemplo
(24) Use o teste da raz˜o e determine se a s´rie ´ absolutamente convergente, condicionalmente
a
e e
convergente, divergente ou se o teste ´ inconclusivo.
e
∞ 1
∞ 1
∞
∞ n!
∞
n!
n
b)
a)
c)
(−1)n+1 2
d)
e)
(−1)n+1
2
n
n
2n − 1
n=1 n
n=1 n!
n=1
n=1 2
n=1
2.13
Teste de Ra´
ız
∞
Teorema 16 (Crit´rio de Cauchy). Seja
e
an uma s´rie de termos n˜o nulos.
e
a
n=1
Seja lim
n
n→∞
|an | = L.
(a) Se L < 1 ent˜o a s´rie ´ absolutamente convergente.
a
e e
(b) Se L > 1 ou L = +∞ ent˜o a s´rie diverge.
a
e
(c) Se L = 1 nada se pode concluir.
Exemplo
ız
e
(25) Ache lim n |an | e use o teste da ra´ para determinar se a s´rie converge, divergente ou se o
n→∞
teste ´ inconclusivo.
e
∞ 2n
∞ [ln(n)]n
∞
(−1)n
b)
c)
a)
n
2
n/2
n=1 n
n=1 n
n=1 [ln(n + 1)]
15

18. ´
SERIE
TESTE
ˆ
CONVERGENCIA
ˆ
ou DIVERGENCIA
´
COMENTARIOS
Diverge se lim an = 0
Inconclusivo
∞
an
Termo Geral
n→∞
n=1
se lim an = 0.
∞
ar
S´rie Geom´trica
e
e
n−1
n=1
a
se |r| < 1.
Converge para s =
1−r
Diverge se |r| ≥ 1
∞
1
p
n=1 n
S´rie-p
e
Converge se p > 1
Diverge se p ≤ 1
∞
∞
an ,
n=1
bn
(i) Se
∞
bn converge, ent˜o
a
an
n=1
Compara¸ao
c˜
compara¸ao.
c˜
´
Util para testes de
compara¸ao.
c˜
∞
n=1
n→∞
´
Util para testes de
n=1
A s´rie de compara¸ao
e
c˜
∞
bn ´, em geral, s´rie
e
e
converge.
∞
an , bn > 0, an ≤ bn
n=1
∞
(ii) Se
an diverge, ent˜o
a
n=1
bn
geom´trica ou s´rie-p.
e
e
n=1
diverge.
∞
∞
Compara¸ao
c˜
an ,
n=1
por Limite
n=1
an , bn > 0
∞
S´ries Alternadas
e
bn
(−1)n an
an
=k>0
bn
(i) as duas s´ries s˜o ambas
e
a
convergentes ou divergentes.
Se lim
n→∞
an > 0
Aplic´vel somente
a
e se an ≥ an+1 ∀n.
as s´ries alternadas.
e
n→∞
∞
Absolutamente
∞
an
n=1
|an | converge
Se
n=1
Convergente
apenas os termos de an
que tˆm maior efeito
e
sobre a magnitude.
Converge se lim an = 0
n=1
(Leibniz)
Para achar bn considere
´
Util para s´ries que
e
∞
ent˜o
a
an converge.
tˆm termos positivos
e
n=1
e termos negativos.
∞
Raz˜o
a
an
n=1
(D’Alembert)
∞
Ra´
ız
an
n=1
an+1
´
= L (ou ∞) a S´rie
e
Util se an envolve
n→∞
an
(i) Converge (absolutamente) se L < 1. fatoriais ou
(ii) Diverge se L > 1 (ou ∞).
potˆncias de grau n.
e
(iii) Inconclusivo se L = 1.
´
Util se an envolve
Se lim n |an | = L (ou ∞) a S´rie
e
Se lim
n→∞
(i) Converge (absolutamente) se L < 1. potˆncias de grau n.
e
(ii) Diverge se L > 1 (ou ∞).
(iii) Inconclusivo se L = 1.
(Cauchy)
∞
an
Integral
(i) Converge se
n=1
an = f (n)
(ii) Diverge se
16
∞
f (x)dx converge.
1
∞
f (x)dx diverge.
1
f (x) obtida de f (n)
deve ser: positiva;
cont´
ınua e decrescente
∀ x ≥ 1.

19. Lista 12: S´ries
e
(A) Determine se cada uma das s´ries abaixo ´ convergente ou divergente:
e
e
∞
1
n=1
2n−1
1.
3
cos( 2 π) + 2
3.
3n
n=1
∞
∞
1
2.
n=1 n + 4
∞
∞
1
4.
n=1 4n
1
1
+ n
4n 4
5.
n=1
∞
∞
1
10.
2
1/3
n=1 (n + 2)
n+2
11.
(−1)
n(n + 1)
n=1
1
cos( 3 nπ)
13.
n2
n=1
14.
∞
∞
16.
n=1
√
3
∞
1
n=1 n!
n3
9.
n=1 n!
1
√
8.
n
n=1
∞
6.
∞
∞
4
7.
n+1
n=1 3
∞
n
(−1)n+1
n=1
n
2n
3n2 + 5n
17.
n 2
n=1 2 (n + 1)
∞
12.
n=1
∞
15.
n2 + 1
(−1)n
n=1
∞
1
(−1)n+1
2
3n
en
n!
∞
18.
n
n=1 ln(n + 1)
(B) Determine se a s´rie dada ´ absolutamente convergente, condicionalmente
e
e
convergente ou divergente.
n
n+1 2
∞
(−1)
1.
n=1
∞
3.
(−1)n
n=1
n!
n2 + 1
n3
n2
2.
n=1 n!
∞
∞
4.
(−1)n+1
n=1
1
n(ln n)2
(C) Calcule s1 , s2 , s3 e sn e depois calcule a soma da s´rie, caso seja convergente.
e
∞
2
1.
−
n=1 (2n + 5)(2n + 3)
∞
2.
∞
n
3.
ln
n+1
n=1
1
2
n=1 4n − 1
∞
√
4.
n=1
17
1
√
n+1+ n

20. (D) Use o teste de divergˆncia para determinar se a s´rie diverge, ou se ´ necess´ria uma invese
e
e
a
tiga¸ao adicional.
c˜
∞
∞
1.
3n
n=1 5n − 1
2.
∞
4.
∞
1
n+1
n=1 e
∞
7.
n=1
∞
1
n
n=1 1 + (0, 3)
5.
3.
n=1
n=1
1
+3
∞
2n
1
+ n
7n − 5 4
ln
n2
n
n=1 ln(n + 1)
6.
∞
1
√
n
e
8.
n sen(1/n)
n=1
(E) Utilize s´ries conhecidas, convergentes ou divergentes, juntamente com as propriedades de
e
s´ries (P1)-(P4) para determinar se a s´rie ´ convergente ou divergente. No caso de convergˆncia,
e
e e
e
determine a soma.
∞
1.
n=3
∞
3.
n=1
1
4
n
+
3
4
n
∞
2.
(2−n − 2−3n )
n=1
∞
1
1
+
n
8
n(n + 1)
n
3
2
4.
n=1
+
2
3
n
(F) Use o teste da integral para determinar se a s´rie converge ou diverge.
e
∞
1.
∞
1
2
n=1 (3 + 2n)
n2 e−n
2.
∞
2
1
2
n=2 n(ln n)
3.
n=1
∞
4.
n=1
n2
n
+1
(G) Use o teste b´sico de compara¸˜o (Teorema 11) para determinar se a s´rie converge ou diverge.
a
ca
e
√
n
2.
2+1
n=1 n
∞
∞
1
1.
4 + n2 + 1
n=1 n
∞
3.
1
n
n=1 n3
∞
4.
2 + cos n
n2
n=1
(H) Use a forma limite do teste da compara¸ao (Teorema 12) para determinar se a s´rie converge
c˜
e
ou diverge.
√
n
1.
n=1 n + 4
∞
∞
2.
2
√
n
n=1 3 +
∞
3.
1
√
4n3 − 5n
n=2
18
8n2 − 7
n
2
n=1 e (n + 1)
∞
4.

21. an+1
e use o teste da raz˜o para determinar se a s´rie converge, diverge ou
a
e
an
se o teste ´ inconclusivo.
e
√
∞
∞ n10 + 10
∞
∞
3n + 1
2n−1
3n
4.
3.
1.
2.
2
2n
n!
5n (n + 1)
n=1
n=1
n=1
n=1 n + 4
(I) Determine lim
n→∞
√
(J) Determine lim n an e use o teste da ra´ para determinar se a s´rie converge, diverge ou se o
ız
e
n→∞
teste ´ inconclusivo.
e
∞
1.
(ln n)n
n/2
n=1 n
∞
1
n
n=1 n
2.
2n
2
n=1 n
∞
3.
∞
4.
n
n
n=1 3
(K) Determine se as s´ries alternadas seguintes convergem ou divergem.
e
∞
1.
(−1)n−1
n=1
∞
4.
(−1)n
n=1
1
2+7
n
∞
2.
∞
(−1)n−1 n5−n
3.
n=1
(−1)n (1 + e−n )
n=1
e2n + 1
e2n
(L) Determine se a s´rie ´ absolutamente convergente, condicionalmente convergente ou divere e
gente.
∞
1.
(−1)n−1 √
n=1
∞
4.
(−1)n
n=1
1
2n + 1
cos( nπ )
6
n2
n=1
∞
2.
21/n
n!
19
∞
3.
(2n − 1)π
1
sen
2
n=1 n