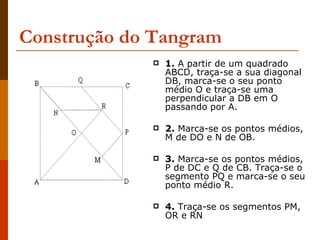
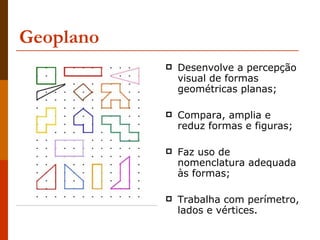
O documento discute os objetivos e materiais concretos utilizados no ensino da matemática. Ele descreve como esses materiais como o ábaco, material dourado, Cuisenaire, tangram e geoplano podem auxiliar na aprendizagem de conceitos matemáticos de forma estimulante e criativa. O documento também discute as competências desejadas para professores de matemática.

1. Educação Matemática Materiais Concretos Alessandra Gonçalves Marrissom Rodrigues Giovanni Almeida

2. Finalidades da Educação Matemática Fazer com que os alunos ultrapassem barreiras do seu desenvolvimento em termos de educação e emprego, quer no sentido de aumentar a sua auto-determinação e o seu envolvimento crítico na cidadania social.

3. Objetivos e metas da Educação Matemática Construção de uma cidadania informada e detentora de sentido crítico Múltiplas relações e determinações entre ensino , aprendizagem e conhecimento matemático . Melhoria da qualidade do ensino e da aprendizagem da Matemática; Desenvolver a Educação Matemática enquanto campo de investigação e produção de conhecimentos.

4. Competências e habilidades do futuro professor de matemática Formar um aluno que corresponda e se adapte, sobremaneira, às transformações econômicas, tecnológicas, políticas e sociais da sociedade mundial contemporânea; Ter domínio dos conteúdos e de seus significados em diferentes contextos, visando a articulação interdisciplinar e a adequação às características de desenvolvimento mental, sociocultural e afetiva dos alunos; Ter domínio das metodologias de ensino correspondentes aos conteúdos; Ter clareza dos objetivos propostos, considerando o desenvolvimento de capacidades cognitivas, afetivas e das habilidades de pensar e aprender.

5. Materiais Concretos: uma alternativa metodológica Recurso auxiliar para o ensino e aprendizagem que permite a aproximação com o objeto que se quer conhecer Fonte estimuladora do raciocínio e da criatividade, afastando-se da transmissão de conhecimentos, dos exercícios prontos e acabados e da repetição exaustiva Segundo Piaget, a aprendizagem da matemática envolve o conhecimento físico e o lógico-matemático.

6. Tipos de Materiais Concretos Os não-estruturados – bolas de gude, carretéis, tampinhas de garrafa, palitos de sorvete – não têm função determinada e seu uso depende da criatividade do professor. Os estruturados apresentam idéias matemáticas definidas. Entre eles temos o ábaco, o geoplano, o material dourado, o material Cuisenaire e o tangran.

7. Ábaco Atividades envolvendo o Sistema de Numeração Decimal, a base 10 e o valor posicional dos algarismos, além das 4 operações (com mais ênfase na adição e na subtração).

8. Material Dourado Montessori Maria Montessori (1870-1952), nasceu na Itália. Estudou as crianças com deficiências psíquicas Desenvolveu alguns materiais para trabalhar diversos aspectos cognitivos na criança

9. Material Dourado Montessori Destina-se a atividades que auxiliam o ensino e a aprendizagem do sistema de numeração decimal-posicional e dos métodos para efetuar as operações fundamentais

10. Material Dourado Montessori É constituído por cubinhos, barras, placas e cubão, que representam:

11. Material Cuisenaire É constituído por uma série de barras de madeira, sem divisão em unidades e com tamanhos variando de uma até dez unidades. Cada tamanho corresponde a uma cor específica.

12. Material Cuisenaire O material auxilia na compreensão da sucessão de números naturais; Na decomposição de uma adição em diferentes parcelas; Nas atividades, os conceitos trabalhados são: sucessor, antecessor, estar entre, antes de, depois de, maior e menor.

13. Tangram Trabalha a análise e síntese; A regra básica é que cada figura formada deve incluir as sete peças; Familiariza o aluno com as figuras básicas da Geometria; Desenvolve o raciocínio lógico para a resolução de problemas, coordenação motora e habilidades na utilização dos materiais a serem utilizados.

14. Construção do Tangram 1. A partir de um quadrado ABCD, traça-se a sua diagonal DB, marca-se o seu ponto médio O e traça-se uma perpendicular a DB em O passando por A. 2. Marca-se os pontos médios, M de DO e N de OB. 3. Marca-se os pontos médios, P de DC e Q de CB. Traça-se o segmento PQ e marca-se o seu ponto médio R. 4. Traça-se os segmentos PM, OR e RN

15. Geoplano Desenvolve a percepção visual de formas geométricas planas; Compara, amplia e reduz formas e figuras; Faz uso de nomenclatura adequada às formas; Trabalha com perímetro, lados e vértices.

16. Transcrição da atividade GEOPLANO Que figura é essa? Material: - Geoplano - Elásticos - Espelho - Material para registro

17. Metodologia Esta atividade pode ser realizada em grupo, em duplas, ou individualmente. O professor mostra uma forma que os alunos conheçam e possam reproduzir, mesmo sem saber nomeá-las (quadrado, retângulo, trapézio, etc.). No geoplano, usando 1 elástico, deverão reproduzi-la. O professor pode sugerir que a figura deve ser montada utilizando um n.º de pregos. (se a figura mostrada estiver desenhada na malha pontilhada, facilitará a visualização da quantidade de pregos.)

18. Com a figura montada, o professor questiona o nome da figura; quantos lados ela tem; quantos pregos ela está tocando (possibilitando um 1º contato com a noção de perímetro). A seguir, pergunta o que é preciso fazer para que essa figura fique maior. Deixando-os explorar o geoplano, eles irão deslocar os elásticos para ampliá-la. Depois, pode pedir que a diminuam. Daí, podem surgir questionamentos sobre quantos pregos foram usados na figura maior, e na menor, o que houve com as figuras – se ficaram iguais ou mudaram a forma.

19. Todas as questões podem ser registradas, e num segundo momento, as figuras formadas, desenhadas em quadriculados. Fonte: http://paje.fe.usp.br/~labmat/edm321/1999/material/private/geoplano.htm

20. Materiais Concretos: Pontos positivos Despertam a curiosidade e estimulam o aluno a fazer perguntas, descobrir semelhanças e diferenças, criar hipóteses e a chegar às próprias soluções. Ajuda na organização de idéias e refletir sobre a atividade realizada. Ajuda na coordenação motora; memória; análise-síntese; constância de percepção de forma, tamanho e cores.

21. Pressuposto Espera-se que seja dada a devida importância a um ensino de matemática que estimule o aluno a raciocinar e questionar, para que a aprendizagem não se detenha apenas a fórmulas prontas.

22. Referências Geoplano. Disponível em: <http://paje.fe.usp.br/~labmat/edm321/1999/material/private/geoplano.htm>. Acesso em: 10 de outubro de 2009; Maria Montessori. <http://www.members.tripod.com/pedagogia/infantil/montesori.htm>.Disponivel em: 10 de outubro de 2009; MATOS, J.F. A educação matemática como fenómeno emergente: desafios e perspectivas possíveis. Universidade de Lisboa. Disponível em: <http://www.educ.fc.ul.pt/docentes/jfmatos/comunicacoes/Sem_PA.doc> Acesso em: 07 de outubro de 2009; O profissional em Educação Matemática. Adaptado de Sérgio Lorenzato & Dario Fiorentino, 2001. Universidade Santa Cecília. Disponivel em: <http://sites.unisanta.br/teiadosaber/apostila/matematica/O_profissional_em_Educacao_Matematica-Erica2108.pdf>Acesso em 07 de outubro de 2009; Tangram e o Cabri Geometry . Disponível em: http://www.edumatec.mat.ufrgs.br/atividadesdiversas/ativ06.htm>. Acesso em: 10 de outubro de 2009. Sá, I.P. Materiais Concretospara o ensino da Matemática. Disponivel em:<www.magiadamatematica.com/diversos/eventos/05-concreto1.pps>Universidade Severino Sombra Curso de Pedagogia

23. OBRIGADA!!!