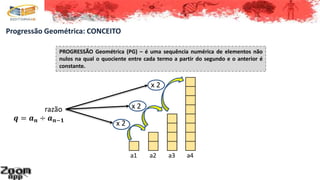
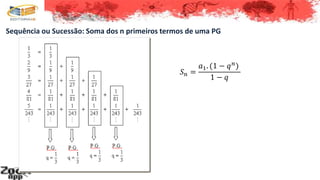
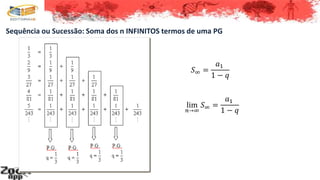
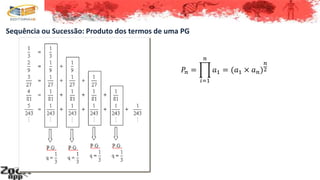
1. O documento discute sequências numéricas, com foco em progressões aritméticas e geométricas; 2. Uma progressão geométrica é uma sequência onde o quociente entre cada termo e o anterior é constante; 3. As propriedades de uma progressão geométrica incluem ter termos intermediários que são médias geométricas dos adjacentes e produtos de termos equidistantes dos extremos iguais ao produto dos extremos.

1. Matemática
Progressão Geométrica

2. Sequências Numéricas:
1. Sequências Numéricas;
a. Sequência ou Sucessão;
b. Leis de Formação;
2. Progressão Aritmética;
a. Conceitos;
b. Razão “r”;
c. Termo Geral;
d. Propriedades de uma PA;
e. Interpolação;
f. Soma dos n primeiros termos de uma PA;
3. Progressão Geométrica;
a. Condição de Existência;
b. Razão “q”;
c. Termo Geral;
d. Propriedades de uma PG;
e. Interpolação;
f. Soma dos n primeiros termos de uma PG;
g. Soma dos Infinitos termos de uma PG.

3. a1 a2 a3 a4
PROGRESSÃO Geométrica (PG) – é uma sequência numérica de elementos não
nulos na qual o quociente entre cada termo a partir do segundo e o anterior é
constante.
Progressão Geométrica: CONCEITO
x 2
x 2
x 2
razão
𝒒 = 𝒂 𝒏 ÷ 𝒂 𝒏−𝟏

4. Progressão Geométrica: Termo Geral de uma PG

5. Sequência ou Sucessão: PROPRIEDADES DE UMA PG
Em qualquer P.G., cada termo,
exceto os extremos, é a média
geométrica entre o
precedente e o consequente.
𝑎 𝑘
2
= 𝑎 𝑘−1. 𝑎 𝑘+1 𝑜𝑢
𝑎 𝑘 = 𝑎 𝑘−1. 𝑎 𝑘+1
Em qualquer P.G., o produto
dos termos equidistantes dos
extremos é igual ao produto
dos extremos.
𝑎 𝑘−1. 𝑎 𝑘+1 = 𝑎1. 𝑎 𝑛
Em uma P.G. de número ímpar
de termos, o termo médio é a
média geométrica entre os
extremos.
𝑇. 𝑀 = 𝑎1. 𝑎 𝑛

6. Sequência ou Sucessão: Interpolação Geométrica
Interpolação Geométrica – Para interpolar (colocar entre polos ou extremos) n
termos entre dois números 𝑎1 𝑒 𝑎 𝑛, de modo a formar uma PG, deve-se usar,
preferencialmente a fórmula do termo geral.
Exemplo: Um objeto foi vendido do dia 1º de janeiro por R$ 100,00 e, três
meses depois, no dia 1º de abril, devido à sua depreciação mensal de seu valor,
foi revendido por R$ 72,90. Qual era o preço desse produto nos primeiros dias
de fevereiro e março?
𝑎1 = 100; 𝑎4 = 72,90.
𝑎 𝑛 = 𝑎1. 𝑞 𝑛−1 → 72,90 = 100. 𝑞3 → 𝑞 =
3 72,90
100
= 0,9 𝑜𝑢 90% 𝑑𝑒 𝑡𝑎𝑥𝑎 𝑑𝑒 𝑑𝑒𝑠𝑐𝑜𝑛𝑡𝑜
𝑎2 = 100 . 0,9 = 90 𝑒 𝑎3 = 100 . (0,9)2= 81

7. Sequência ou Sucessão: Soma dos n primeiros termos de uma PG
𝑆 𝑛 =
𝑎1. (1 − 𝑞 𝑛)
1 − 𝑞

8. Sequência ou Sucessão: Soma dos n INFINITOS termos de uma PG
𝑆∞ =
𝑎1
1 − 𝑞
lim
𝑛→∞
𝑆∞ =
𝑎1
1 − 𝑞

9. Sequência ou Sucessão: Produto dos termos de uma PG
𝑃𝑛 =
𝑖=1
𝑛
𝑎1 = (𝑎1 × 𝑎 𝑛)
𝑛
2

10. Fim da Apresentação.