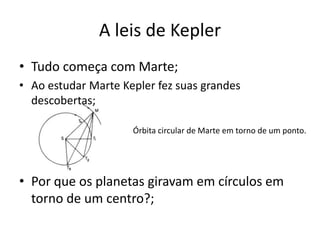
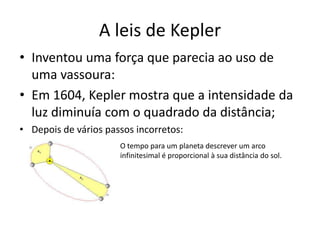
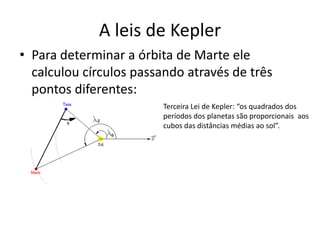
Johannes Kepler (1571-1630) foi um astrônomo alemão que tentou conciliar a visão heliocêntrica de Copérnico com a Bíblia. Ele desenvolveu as três leis de Kepler que descrevem o movimento dos planetas em órbitas elípticas ao redor do Sol. Suas descobertas ajudaram Isaac Newton a formular a lei da gravitação universal.

1. Johannes Kepler
• 27/12/1571-15/11/1630
• Família conturbada;
• Problemas de saúde;
• Inteligência reconhecida;
• Tentou conciliar a visão de Copérnico com a Bíblia;
• 1588-bacharel
• 1591-mestre em Filosofia;
• 1594- Professor de Astronomia e Matemática na
escola luterana de Gratz;

2. • 1595- Ideia brilhante:
• Resultado: a razão entre os raios dos dois círculos era a mesma que
os raios das órbitas de Saturno e Júpiter.
• Tentativas: inscrever no intervalo entre Júpiter e Marte um
quadrado;
• Entre Marte e a Terra um pentágono;
• Entre a Terra e Vênus um hexágono.
• Abandonou as figuras bidimensionais e partiu para as formas
tridimensionais;
considerou um triângulo com um círculo inscrito e
outro circunscrito:

3. • Havia apenas cinco sólidos perfeitos e cinco
intervalos entre os planetas.
 Na órbita de Saturno, inscreveu um
cubo;
 No cubo outra esfera: órbita de Júpiter;
 Na esfera, inscreveu o tetraedro, e
nele a esfera de Marte;
 Entre as esferas de Marte e da Terra
colocou um dodecaedro;
 Entre a terra e Vênus, o icosaedro;
 Entre Vênus e Mercúrio, o octaedro;

4. • Tentou explicar por que as distâncias de cada
planeta ao Sol variam dentro de certos limites;
• Postulou que deveria haver uma força
emanada do sol sobre os planetas
• Primeiro a atribuir uma causa física ao
movimento dos planetas;
• Kepler colocou, assim, o Primeiro Motor de
Aristóteles no Sol;
Animia motrix

5. • Primeiras tentativas para relacionar as
distâncias dos planetas ao Sol ao períodos de
rotação:
• Relação entre períodos de rotação entre dois
planetas e suas distâncias: Rs/R1= T1+Ts/2T1;

6. • Tudo começa com Marte;
• Ao estudar Marte Kepler fez suas grandes
descobertas;
• Por que os planetas giravam em círculos em
torno de um centro?;
A leis de Kepler
Órbita circular de Marte em torno de um ponto.

7. • Ele supôs que cada planeta estava sujeito a
duas forças oposta;
• Quanto maior a distância, menor a força
emanada do Sol;
• Sol centro do seu modelo de sistema;
A leis de Kepler

8. • Primeiro passo: determinar o movimento de
Marte e a forma da própria órbita;
• Determinar a órbita da Terra;
• Mostrou que ela se deslocava com velocidade
variável;
A leis de Kepler

9. • Inventou uma força que parecia ao uso de
uma vassoura:
• Em 1604, Kepler mostra que a intensidade da
luz diminuía com o quadrado da distância;
• Depois de vários passos incorretos:
A leis de Kepler
O tempo para um planeta descrever um arco
infinitesimal é proporcional à sua distância do sol.

10. • Para determinar a órbita de Marte ele
calculou círculos passando através de três
pontos diferentes:
A leis de Kepler
Terceira Lei de Kepler: “os quadrados dos
períodos dos planetas são proporcionais aos
cubos das distâncias médias ao sol”.