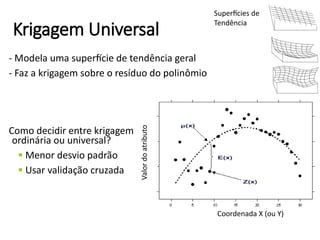
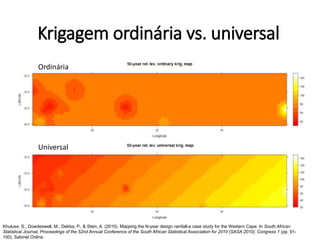
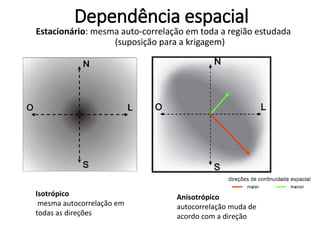
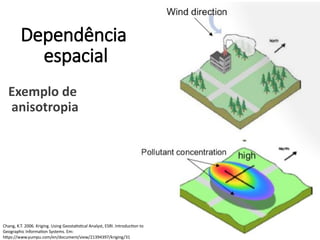
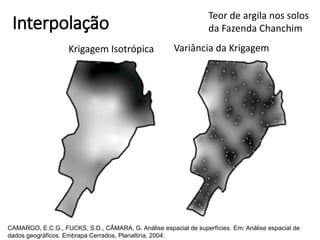
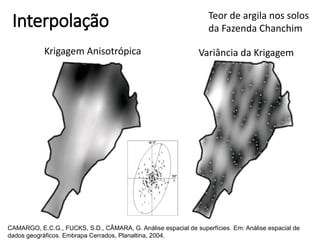
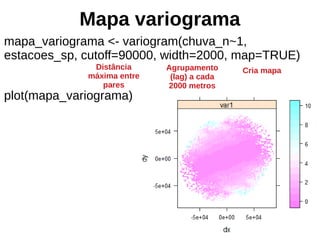
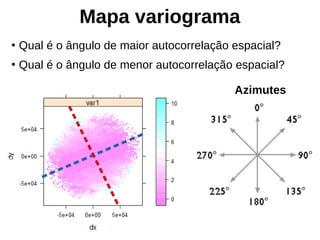
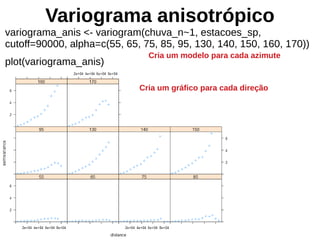
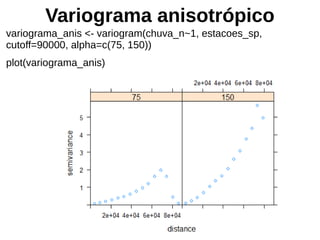
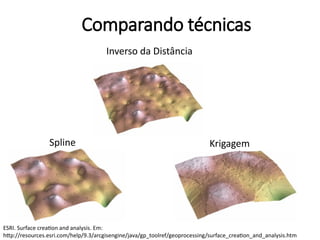
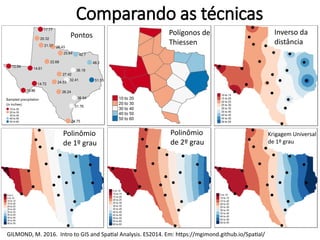
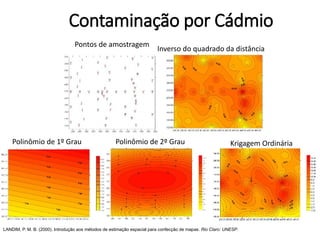
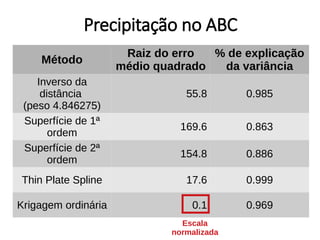
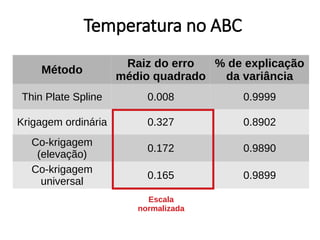
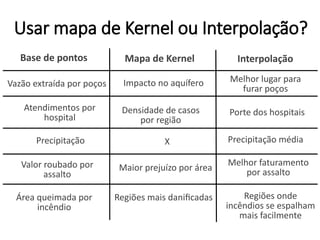
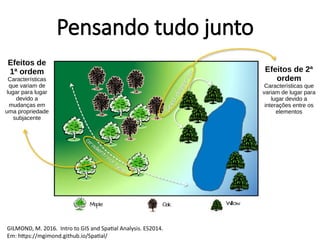
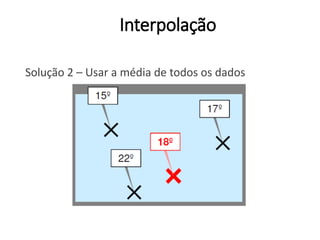
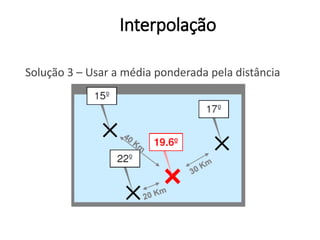
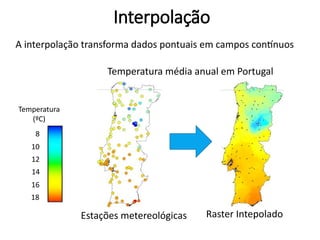
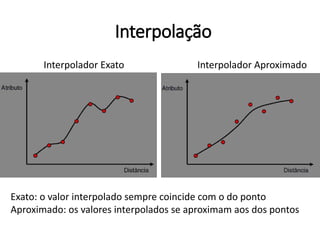
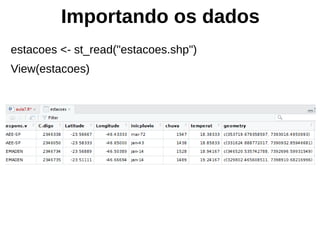
Este documento apresenta uma introdução aos métodos de interpolação e geoestatística no software R. Após uma breve introdução, o documento descreve métodos como vizinho mais próximo, inverso da distância, superfícies de tendência, funções de base radial e krigagem. Referências bibliográficas e tutoriais online são fornecidos para apoiar o aprendizado destes métodos espaciais.









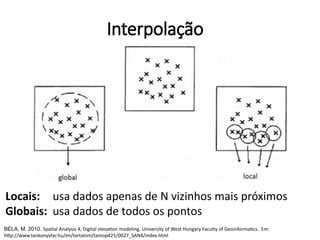




![Vizinho mais próximo - Chuva
plot(voronoi_sf["chuva"], breaks="quantile")](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-31-320.jpg)
![Vizinho mais próximo
Temperatura
plot(voronoi_sf["temperat"], breaks="quantile")](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-32-320.jpg)

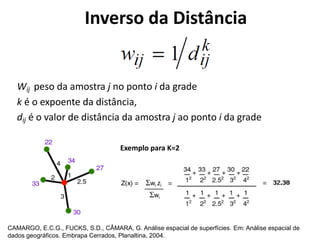
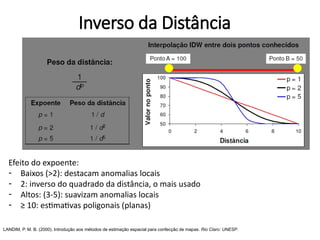
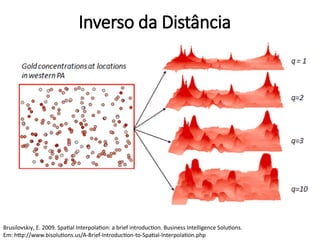
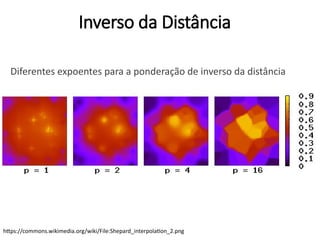



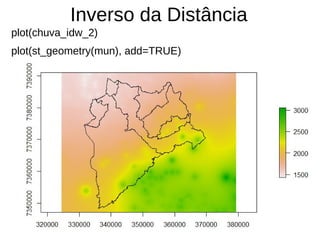
![Inverso da Distância
●
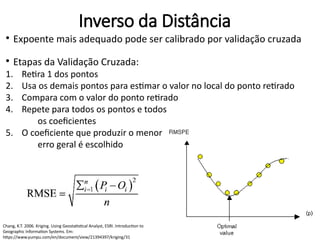
Raiz do erro médio quadrático
(Root Mean Square Error – RMSE) =
sqrt(mean(cv_idw_2$residual^2))
[1] 117.8616
●
Estimativa de % de explicação da variância
(análogo ao R2)
1-(var(cv_idw_2$residual)/var(cv_idw_2$observed))
[1] 0.9360051](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-43-320.jpg)


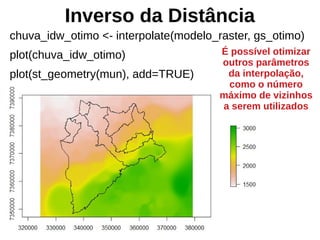
![Otimização da interpoloação
erro_medio_quadrado <- function(peso) {
gs <- gstat(formula=chuva~1, locations=estacoes, set=list(idp=peso))
cv <- gstat.cv(gs)
sqrt(mean(cv$residual^2)) }
erro_medio_quadrado(2)
peso_otimo <- optimize(f=erro_medio_quadrado, interval=c(1,10))
peso_otimo$minimum
peso_otimo$objective
Cria função para otimizar o peso do inverso da distância
Resultado da função
Parâmetro
da função
Limites mínimos e
máximos para o
parâmetro “peso”
[1] 117.8616
[1] 4.846275
Retorna erro quadrático médio
para peso = 2
Retorna peso com menor erro
quadrático médio
Raiz do erro quadrático médio
do peso otimizado
[1] 55.79638](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-47-320.jpg)
![Otimização da interpoloação
gs_otimo <- gstat(formula=chuva~1,
locations=estacoes, set=list(idp=peso_otimo$minimum))
cv_otimo <- gstat.cv(gs_otimo)
1-(var(cv_otimo$residual)/var(cv_otimo$observed))
[1] 0.9853082](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-48-320.jpg)



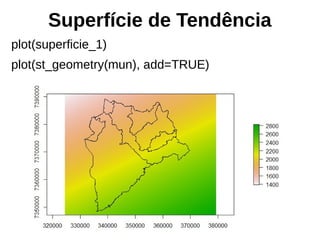
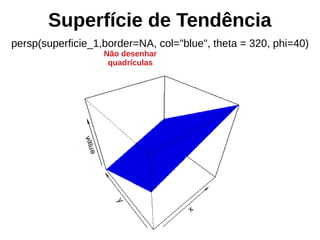
![Superfície de tendência
gs_superficie_1 <- gstat(formula=chuva~1, location=estacoes, degree=1)
Grau da
superfície de
tendência
cv_superficie_1 <- gstat.cv(gs_superficie_1)
sqrt(mean(cv_superficie_1$residual^2))
1-(var(cv_superficie_1$residual)/var(estacoes$chuva))
superficie_1 <- interpolate(modelo_raster, gs_superficie_1)
[1] 169.5668
[1] 0.8627123](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-53-320.jpg)


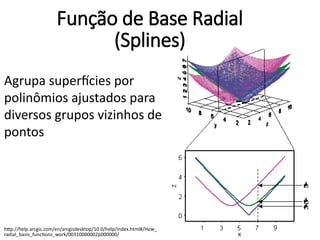
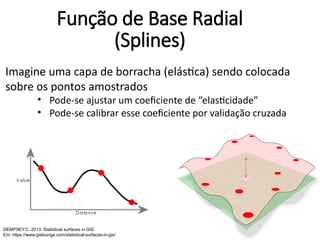
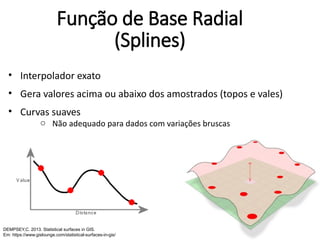
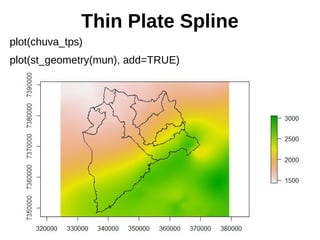
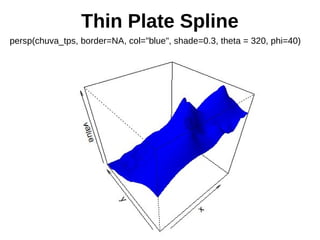
![Thin Plate Spline
install.packages("fields")
library(fields)
modelo_tps <- Tps(x=st_coordinates(estacoes), Y=estacoes$chuva)
sqrt(mean(modelo_tps$residual^2))
1-(var(modelo_tps$residual)/var(estacoes$chuva))
chuva_tps <- interpolate(modelo_raster, modelo_tps)
Variáveis preditoras Variável predita
Erro médio quadrático[1] 17.55077
Funções de spline mais avançadas são
encontradas no pacote geospt
% de explicação
[1,] 0.9985292](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-61-320.jpg)



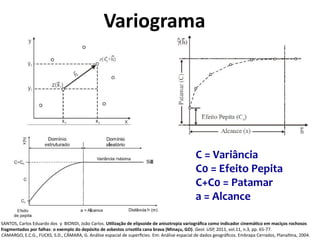
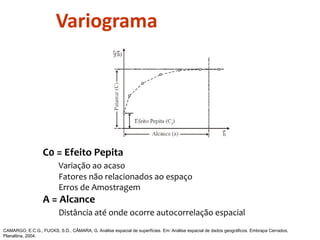
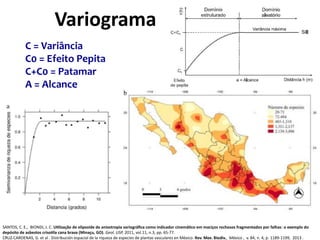
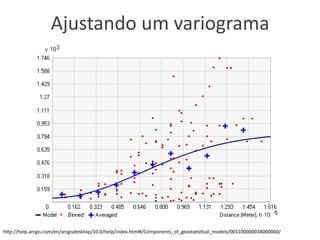
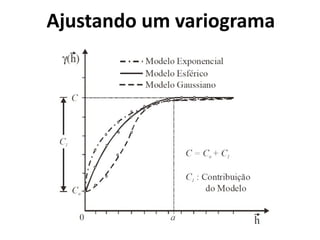
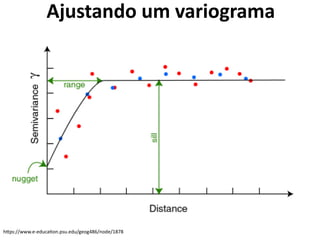
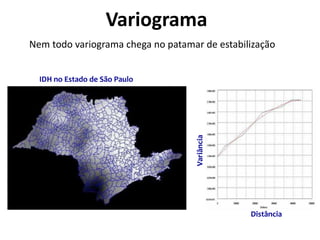

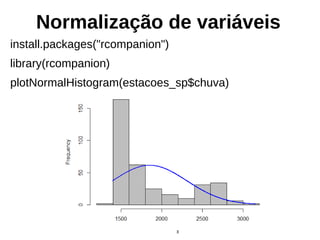

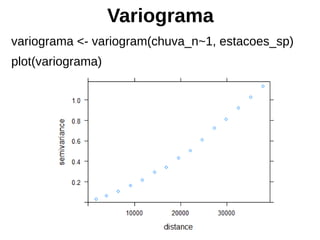
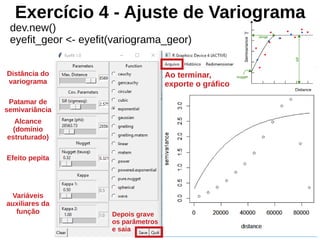
![Variograma
install.packages("geoR")
library("geoR")
estacoes_geodata <- as.geodata(estacoes_sp[,"chuva_n"])
variograma_geor <- variog(estacoes_geodata)
plot(variograma_geor)](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-84-320.jpg)
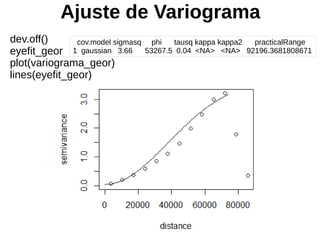
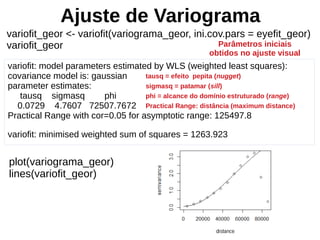
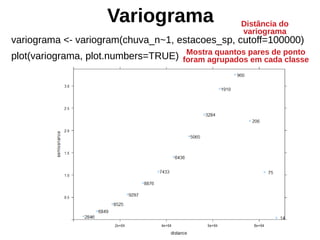
![Ajuste de Variograma
●
Parâmetros obtidos na etapa anterior:
variofit_geor$nugget # efeito pepita
variofit_geor$cov.pars[1] # patamar
variofit_geor$cov.pars[2] # alcance
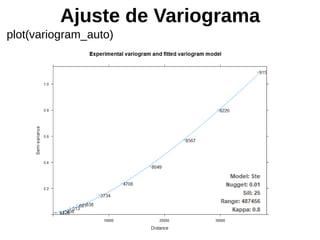
install.packages("automap")
library(automap)
variogram_auto <- autofitVariogram(chuva_n~1, estacoes_sp,
start_vals=c(variofit_geor$nugget, variofit_geor$cov.pars[2],
variofit_geor$cov.pars[1]))
View(variogram_auto$var_model)
[1] 0.07287448
[1] 4.760725
[1] 72507.77
Parâmetros iniciais para ajuste do variograma](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-88-320.jpg)
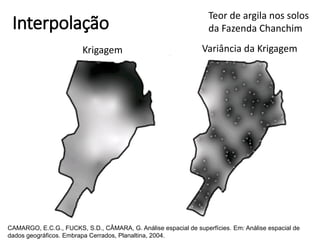
![Krigagem
●
Preparar o modelo raster para formado sp (grid)
writeRaster(modelo_raster,"modelo_raster.tif")
modelo_grid <- readGDAL("modelo_raster.tif")
●
Realizar a krigagem
krigagem_auto = autoKrige(chuva_n~1, estacoes_sp,
new_data = modelo_grid, start_vals = c(variofit_geor$nugget,
variofit_geor$cov.pars[2], variofit_geor$cov.pars[1]))](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-90-320.jpg)
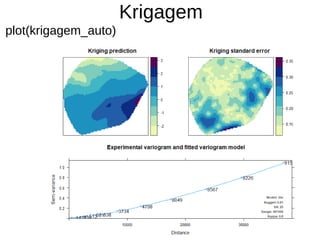
![Krigagem
par(mfrow=c(1,1))
plot(krigagem_auto$krige_output["var1.pred"])](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-92-320.jpg)
![Krigagem
plot(krigagem_auto$krige_output["var1.stdev"])
par(mfrow=c(1,1))](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-93-320.jpg)
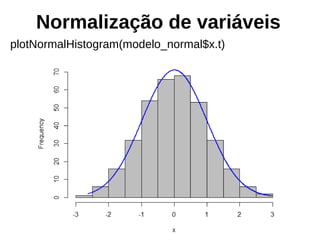
![Converter à escala original
krigagem_auto$krige_output$original <- predict(modelo_normal,
newdata=krigagem_auto$krige_output$var1.pred, inverse=TRUE)
plot(krigagem_auto$krige_output["original"])](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-94-320.jpg)
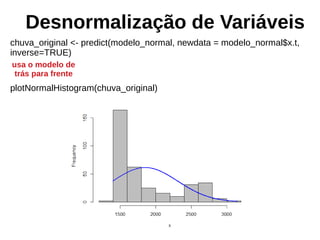
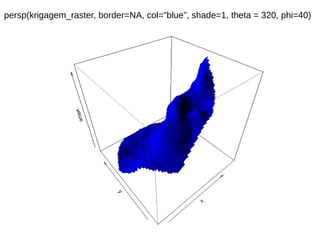
![Exportando para formato raster
krigagem_raster <- raster(krigagem_auto$krige_output["original"])
par(mfrow=c(1,1))
plot(krigagem_raster)
plot(st_geometry(mun), add=TRUE)](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-95-320.jpg)
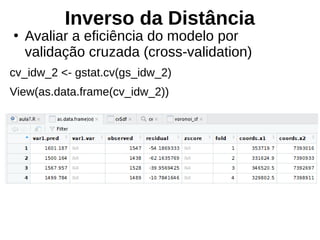
![Validação cruzada da krigagem
krigagem_cv <- autoKrige.cv(chuva_n~1, estacoes_sp,
start_vals=c(variofit_geor$nugget, variofit_geor$cov.pars[2],
variofit_geor$cov.pars[1]))
sqrt(mean(krigagem_cv$krige.cv_output$residual^2))
[1] 0.1710764
Raiz do erro médio quadrado
em escala normalizada
1-(var(krigagem_cv$krige.cv_output$residual)/
var(krigagem_cv$krige.cv_output$observed))
[1] 0.9699433
% de explicação da variância
(adimensional)](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-97-320.jpg)

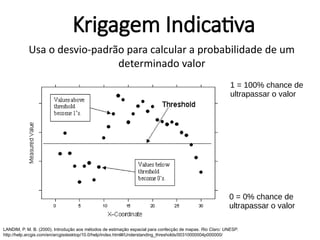
![Krigagem Indicativa
chuva_2000 <- predict(modelo_normal, newdata=2000)
chuva_2000
fit_indicadora <- autofitVariogram(formula=I(chuva_n<chuva_2000)~1,
estacoes_sp)
plot(fit_indicadora)
fit_indicadora$var_model
[1] 0.5810335
model psill range kappa
1 Nug 9.331463e-04 0 0.0
2 Ste 1.007782e+04 19635560 1.1](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-101-320.jpg)
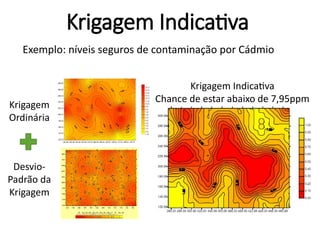
![Krigagem Indicativa
krigagem_indicadora <- krige(formula=I(chuva_n<chuva_2000)~1,
locations=estacoes_sp, model=fit_indicadora$var_model, nmax=12,
newdata=modelo_grid)
plot(krigagem_indicadora["var1.pred"])
plot(st_geometry(mun), add=TRUE)
Máximo de
vizinhos a
interpolar, para
não sobrecarregar
o processador](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-102-320.jpg)

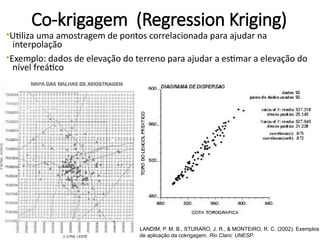
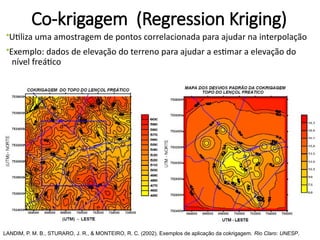
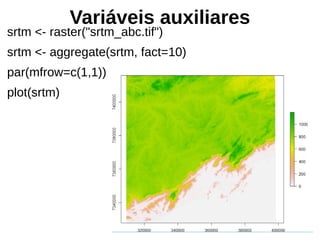
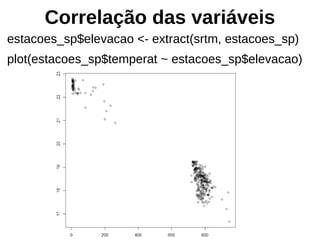

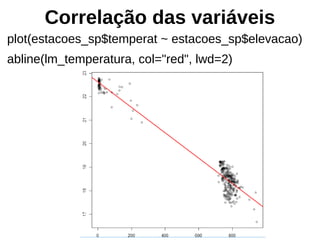
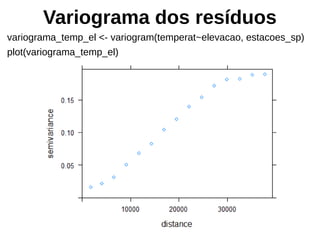
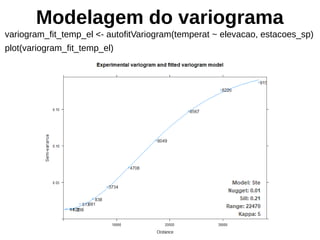

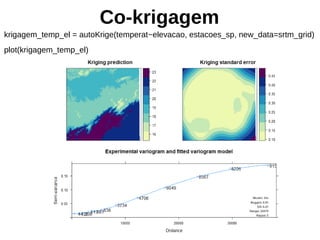
![Validação Cruzada
krigagem_cv_temp_el <- autoKrige.cv(temperat ~ elevacao,
estacoes_sp)
sqrt(mean(krigagem_cv_temp_el$krige.cv_output$residual^2))
[1] 0.1718555
1-(var(krigagem_cv_temp_el$krige.cv_output$residual)/
var(krigagem_cv_temp_el$krige.cv_output$observed))
[1] 0.9890234](https://image.slidesharecdn.com/aula9interpolacao-190418010045/85/Interpolacao-e-Geoestatistica-em-R-114-320.jpg)