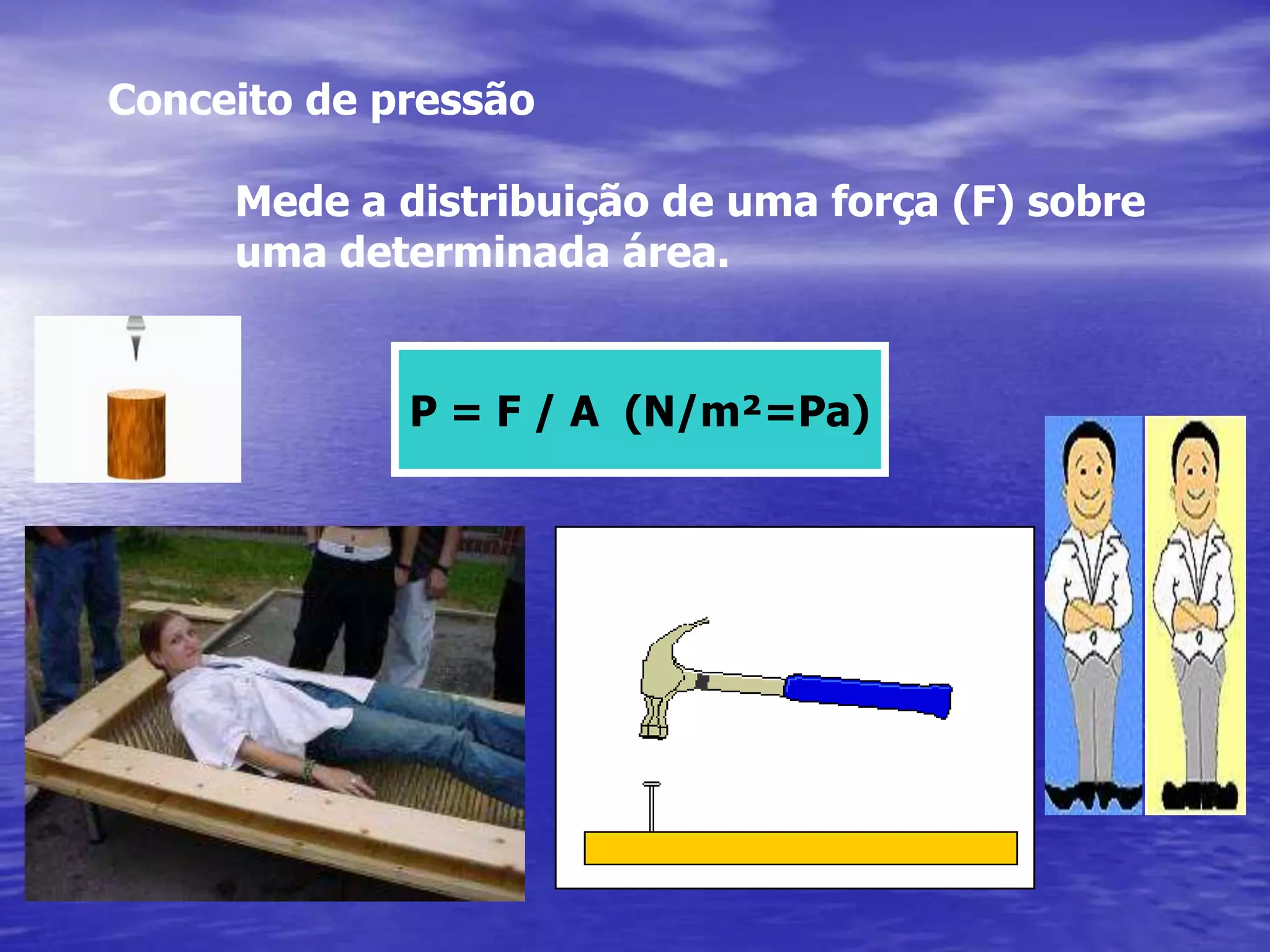
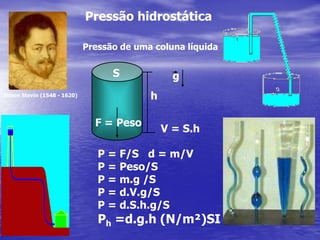
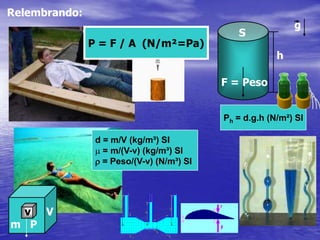
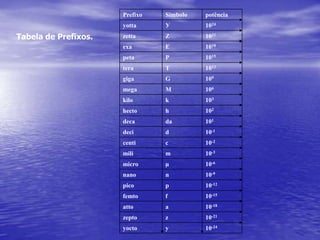
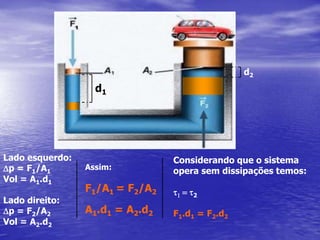
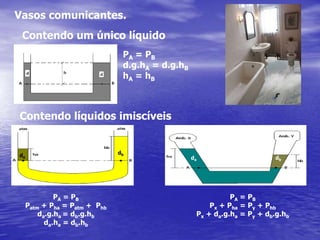
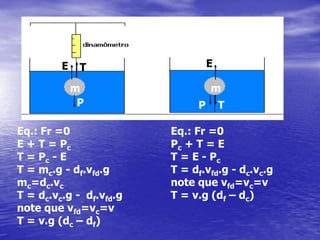
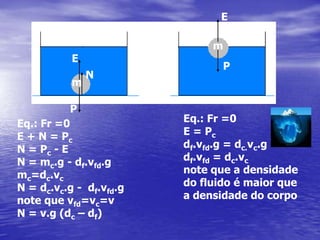
1) O documento apresenta conceitos de pressão, densidade, massa específica e peso específico. 2) São apresentadas equações para calcular pressão, densidade, massa específica e peso específico. 3) Exemplos ilustram aplicações dos conceitos em situações como vasos comunicantes e empuxo.

1. Conceito de pressão Mede a distribuição de uma força (F) sobre uma determinada área.P = F / A (N/m²=Pa)

2. Densidade, Massa específica e Peso específico1) Densidade (d)d = m/V (kg/m³) SIVvvm2) Massa específica (m)v = cavidade com arm = m / (V-v) (kg/m³) SIVvm3) Peso específico (r)r = P/(V-v) (N/m³) SIVVNota:1litro = 10-3m³ = 10³cm³ = 1dm³1mL = 1 cm³P

3. Exemplos1) UFR-RJ A janela de uma casa possui dimensões iguais a 3,0 m × 2,0 m. Em função deum vento forte, a pressão do lado de fora da janela caiu para 0,96 atm, enquanto a pressãodo lado interno manteve-se em 1 atm. O módulo (expresso em 104 N) e o sentido daforça resultante sobre a janela é igual a:Dado: 1 atm = 1 × 105 N/m²a) 6,0; de dentro para fora;b) 4,5; de fora para dentro;c) 2,4; de dentro para fora;d) 9,6; de dentro para fora;e) 2,0; de fora para dentro.fora dentroP = F/SS = 3.2 = 6m²Pf = 0,96.105 N/m²Pd = 1.105 N/m²Fr = S.DPFr =6.(105– 0,96.105)Fr = 6.0,04.105Fr = 2,4.104NResp.: c

4. 2) A pressão no ouvido interno de uma pessoa, no início de uma viagem subindo uma montanha, é igual a 1,010.105 Pa. Admita que essa pressão não varie durante a viagem e que a pressão atmosférica no topo da montanha seja igual a 0,998.105 Pa. Considere o tímpano como uma membrana circular com raio 0,4cm. Em relação ao instante de chegada dessa pessoa ao topo da montanha, quando ainda não foi alcançado novo equilíbrio entre a pressão interna do ouvido e a pressão externa, calcule a força resultante em cada tímpano. Adote π=3.P = F/SPi=1,010.105 Pa; Pf=0,998.105 Pa; R=0,4cm=0,4.10-2 mFr=DP.S ; S = p.R²Fr=(1,010.105-0,998.105).3.(0,4.10-2)²Fr=0,012.105.3.0,16.10-4Fr = 12.10².3.16.10-6Fr = 576.10-4 = 0,0576 NFr ≈ 0,06 N

5. Pressão hidrostáticaPressão de uma coluna líquidaSghSimon Stevin (1548 - 1620)F = PesoV = S.hP = F/S d = m/VP = Peso/SP = m.g /SP = d.V.g/SP = d.S.h.g/SPh =d.g.h (N/m²)SI

6. Teorema de StevinNuma mesma horizontal de um mesmo líquido, em equilíbrio, todos os pontos estão submetidos a mesma pressão.Py – Px = d.g (h-h’)DP = d.g.Dhh’Relação entre PA e PBDP = d.g.DhPA – PB = d.g.(hA – hB)hA = hB = hPA = PBxhDhya b Pa > PbA B

7. Exemplos:1) UFMT Ao projetar o sistema de fornecimento de água de uma cidade, um técnico temque dimensionar as caixas d’água de cada bairro, levando em conta as leis da Física.Acerca da maneira mais adequada de desenvolver tal projeto, julgue os itens.( ) O técnico deve projetar caixas d’água tanto mais largas quanto mais longe, emmédia, estiverem as residências.( ) Caixas d’água de diferentes formatos apresentam diferentes eficiência quanto aofornecimento de água.( ) Num sistema de abastecimento de água onde nenhuma bomba está presente, o agentefísico responsável pela pressão da água nos canos é a força da gravidade.( ) A pressão da água no interior da tubulação de uma residência independe do diâmetro dos canos.FFVV

8. 2) UEMS Sobre a água do reservatório representado na figura, existe ar rarefeito sob pressãode 8,0.10³ N/m², e um êmbolo de peso 80 N, com faces de área 400 cm². Sendom= 1000 kg/m³, a massa específica da água e 10m/s² a aceleração da gravidade, calcule,desprezando o atrito no êmbolo, a pressão p no ponto P:Pp= Par+Pe+PhPp = 8.10³ + 80 +10³.10.1 4.10-2Pp = 8.10³+2.10³+10.10³Pp = 2.104N/m²extra:Considerando que a face da rolha tem área de 2cm²,calcule a força que a mesma suporta.P = F/SF = P.SF = 2.104.2.10-4F = 2N

9. Relembrando:gSP = F / A (N/m²=Pa)hF = PesoPh = d.g.h (N/m²) SId = m/V (kg/m³) SI =m/(V-v) (kg/m³) SIr = Peso/(V-v) (N/m³) SIVvm P

10. Prensa e elevador hidráulicosBlaise Pascal (1623-1662)Princípio de Pascal:O acréscimo de pressão numa região de um fluido, em equilíbrio, transmite-se igualmente para as demais regiões do fluido e para as paredes do recipiente que o contém.

11. d2d1Lado esquerdo:Dp = F1/A1Vol = A1.d1Lado direito:Dp = F2/A2Vol = A2.d2Considerando que o sistemaopera sem dissipações temos:t1 = t2F1.d1 = F2.d2Assim:F1/A1 = F2/A2A1.d1 = A2.d2

12. Exemplos :1) UFRN O princípio de Pascal diz que qualquer aumento de pressão num fluido se transmiteintegralmente a todo o fluido e às paredes do recipiente que o contém. Uma experiênciasimples pode ser realizada, até mesmo em casa, para verificar esse princípio e ainfluência da pressão atmosférica sobre fluidos. São feitos três furos, todos do mesmodiâmetro, na vertical, na metade superior de uma garrafa plástica de refrigerante vazia,com um deles a meia distância dos outros dois. A seguir, enche-se a garrafa com água,até um determinado nível acima do furo superior; tampa-se a garrafa, vedando-se totalmenteo gargalo, e coloca-se a mesma em pé, sobre uma superfície horizontal.A seguir, estão ilustradas quatro situações para representar como ocorreria o escoamentoinicial da água através dos furos, após efetuarem-se todos esses procedimentos.Assinale a opção correspondente ao que ocorrerá na prática.Resp.: a)

13. 2) UERJ Um adestrador quer saber o peso de um elefante. Utilizando uma prensa hidráulica,consegue equilibrar o elefante sobre um pistão de 2000 cm2 de área, exercendo umaforça vertical F equivalente a 200 N, de cima para baixo, sobre o outro pistão da prensa,cuja área é igual a 25 cm2. Calcule a massa do elefante. Adote g = 10m/s2F1/A1 = F2/A2P/2000 = 200/25P = 400000/25P = 16000 NP = m.g16000 = m.10m = 1600 kg

14. 3) (UFCE) Na “redução” vista na figura, determine, em m/s, a velocidade de escoamento de um líquido suposto ideal, no trecho CD,sabendo que no trecho AB a velocidade é de 4m/s. dados: S1=21cm²; S2=3,5cm².VolAB=VolDCS1.ΔSAB=S2.ΔSCDV=ΔS/ΔtS1.VAB.Δt= S2.VCD.Δt21.4=3,5.VCDVCD=24m/s

15. Algumas unidades de medida de pressãoAplicando o Teorema de Stevintemos:PA = PBPar = d.g.hPara o nível do mar com t=0ºCe sendo g = 9,8 m/s², temos:dHg = 13,6.10³ kg/m³Par = 13,6.10³.9,8.0,76Par ≈ 1,013.105N/m²Evangelista Torricelli (1608 - 1647) A BAdotando como referência o nível do mar e t=0ºC, temos: 1atm ≈ 1,013.105N/m² (Pa) 1atm = 76cmHg = 760mmHg = 10mH2O

16. Vasos comunicantes.Contendo um único líquidoPA = PBd.g.hA = d.g.hBhA = hBContendo líquidos imiscíveisdbdada dbPA = PBPatm + Pha = Patm + Phbda.g.ha = db.g.hbda.ha = db.hbPA = PBPx + Pha = Py + PhbPx + da.g.ha = Py + db.g.hb

17. Exemplos1) UFRJ Um tubo em U, aberto em ambos os ramos, contém dois líquidos não miscíveisem equilíbrio hidrostático. Observe, como mostra a figura, que a altura da coluna dolíquido (1) é de 34 cm e que a diferença de nível entre a superfície livre do líquido (2), noramo da direita, e a superfície de separação dos líquidos, no ramo da esquerda, é de2,0 cm.Considere a densidade do líquido (1) igual a 0,80 g/cm³.Calcule a densidade do líquido (2).P1 = P2d1.h1 = d2.h20,8.34 = d2.2d2 = 13,6 g/cm³ou d2 = 13,6.10³ kg/m³

18. Empuxo: Todo corpo imerso em um fluidoexperimenta uma força vertical em seucentro de massa, orientada da região de maior pressão para região de menor pressão, cuja intensidade corresponde aopeso do volume de fluido deslocado.Arquimedes (282 - 212 a.C.)E = PfdE = mfd.gd = m/vE = df.vfd.g (N) SINote que o volume do fluido deslocado corresponde ao volumedo corpo que está imersovfd

19. Confronto entre empuxo e peso de um corpo.Eq.: Fr =0E = Pcdf.vfd.g = mc.gmc=dc.vcdf.vfd.g = dc.vc.gnote que vfd=vcdf=dcEmdP

20. EETm m PP TEq.: Fr =0E + T = PcT = Pc - ET = mc.g - df.vfd.gmc=dc.vcT = dc.vc.g - df.vfd.gnote que vfd=vc=vT = v.g (dc – df)Eq.: Fr =0Pc + T = ET = E - PcT = df.vfd.g - dc.vc.gnote que vfd=vc=vT = v.g (df – dc)

21. EmEPNm PEq.: Fr =0E = Pcdf.vfd.g = dc.vc.gdf.vfd = dc.vcnote que a densidadedo fluido é maior quea densidade do corpoEq.: Fr =0E + N = PcN = Pc - EN = mc.g - df.vfd.gmc=dc.vcN = dc.vc.g - df.vfd.gnote que vfd=vc=vN = v.g (dc – df)

22. 4) Fuvest-SP Um motorista pára em um posto e pede ao frentista para regular a pressão dos pneus de seu carro em 25 “libras” (abreviação da unidade “libra” força por polegada quadrada ou “psi”). Essa unidade corresponde à pressão exercida por uma força igual ao peso da massa de 1 libra, distribuída sobre uma área de 1 polegada quadrada. Uma libra corresponde a 0,5 kg e 1 polegada a 25 x 10–3 m, aproximadamente. Como 1 atm corresponde a cerca de 1 x 105 Pa no SI (e 1 Pa = 1 N/m²), aquelas 25 “libras” pedidas pelo motorista equivalem aproximadamente a:a) 2 atm b) 1 atm c) 0,5 atm d) 0,2 atm e) 0,01 atmPpneu = 25 libras1libra = 0,5 kg1polegada = 25.10-3m1atm=105N/m²25libras=12,5kgF = 125 NS = (1polegada)² = (25.10-3)²P = 125/625.10-6P = 2.105N/m²P = 2atm

23. 5) A pressão no ouvido interno de uma pessoa, no início de uma viagem subindo uma montanha, é igual a 1,010.105 Pa. Admita que essa pressão não varie durante a viagem e que a pressão atmosférica no topo da montanha seja igual a 0,998.105 Pa. Considere o tímpano como uma membrana circular com raio 0,4cm. Em relação ao instante de chegada dessa pessoa ao topo da montanha, quando ainda não foi alcançado novo equilíbrio entre a pressão interna do ouvido e a pressão externa, calcule a força resultante em cada tímpano. Adote π=3.P = F/SPi=1,010.105 Pa; Pf=0,998.105 Pa; R=0,4cm=0,4.10-2 mFr=DP.S ; S = p.R²Fr=(1,010.105-0,998.105).3.(0,4.10-2)²Fr=0,012.105.3.0,16.10-4Fr = 12.10².3.16.10-6Fr = 576.10-4 = 0,0576 NFr ≈ 0,06 N

24. 6) A anestesia peridural consiste em injetar líquido anestésico numa região próxima à medula espinhal do paciente. Para procurar a região exata, o anestesista introduz uma agulha com uma seringa, sem anestésico e com o embolo na posição A da figura, até que o êmbolo seja sugado espontaneamente.Isso significa que, nesta região:a) A temperatura é maior que no restante do corpo.b) A densidade é menor que no restante do corpo.c) A pressão é menor que a pressão atmosférica.d) Só existem líquidos orgânicose) Predominam tecidos sólidosresp.: c)

25. 7) Dois líquidos que não se misturam são colocados em um tubo aberto conforme representa a figura:1 2Considerando-se que dA e dB são as respectivas densidades, determine a razão dB/dA.P1 = P2dA.g.hA = dB.g.hBdB/dA = hA/hBdB/dA = 30/10 dB/dA = 3

26. Extra:1) UFMT Ao projetar o sistema de fornecimento de água de uma cidade, um técnico temque dimensionar as caixas d’água de cada bairro, levando em conta as leis da Física.Acerca da maneira mais adequada de desenvolver tal projeto, julgue os itens.( ) O técnico deve projetar caixas d’água tanto mais largas quanto mais longe, emmédia, estiverem as residências.( ) Caixas d’água de diferentes formatos apresentam diferentes eficiência quanto aofornecimento de água.( ) Num sistema de abastecimento de água onde nenhuma bomba está presente, o agentefísico responsável pela pressão da água nos canos é a força da gravidade.( ) A pressão da água no interior da tubulação de uma residência independe do diâmetro dos canos.FFVV

27. 2) UEMS Sobre a água do reservatório representado na figura, existe ar rarefeito sob pressãode 8,0.10³ N/m², e um êmbolo de peso 80 N, com faces de área 400 cm². Sendom= 1000 kg/m³, a massa específica da água e 10m/s² a aceleração da gravidade, calcule,desprezando o atrito no êmbolo, a pressão p no ponto P:Pp= Par+Pe+PhPp = 8.10³ + 80 +10³.10.1 4.10-2Pp = 8.10³+2.10³+10.10³Pp = 2.104N/m²extra:Considerando que a face da rolha tem área de 2cm²,calcule a força que a mesma suporta.P = F/SF = P.SF = 2.104.2.10-4F = 2N

28. 3) Unifor-CE Um mergulhador que submerge até uma profundidade de 28 m, na água,experimenta um aumento de pressão, em atmosferas, igual a:a) 28 d) 2,8b) 14 e) 1,4c) 7,0Dados:Pressão atmosférica: 1,0 atm = 1,0 . 105 N/m²Aceleração da gravidade: g = 10 m/s²Densidade da água: d = 1,0 g/cm³P = d.g.hP = 10³.10.28P = 2,8.105 N/m²1 atm = 105 N/m²x _____2,8.105x = 2,8 atmresp.: d

29. Extras1) F.M. Itajubá-MG 2 (dois) litros de um líquido com densidade igual a 0,500 g/cm³ sãomisturados a 6 (seis) litros de outro líquido com densidade igual a 0,800 g/cm³. Se na mistura não ocorreu contração de volume, determine, em g/cm³, qual a densidade do líquido resultante da mistura acima descrita.a) 0,725 b) 0,300 c) 0,415 d) 0,375 e) 0,6152) U.E. Londrina-PR A torneira de uma cozinha é alimentada pela água vinda de umreservatório instalado no último pavimento de um edifício. A superfície livre da água no reservatório encontra-se 15 m acima do nível da torneira. Considerando que a torneira esteja fechada, que a aceleração da gravidade seja de 10 m/s² e que a massa específica da água seja igual a 1,0 g/cm³, a pressão que a água exerce sobre a torneira é, em atm? dado: 1 atm = 105N/m².3) U.F. Pelotas-RS Um mergulhador cuidadoso mergulha, levando no pulso um aparelho capaz de registrar a pressão total a que esta submetido. Em um determinado instante, durante o mergulho, o aparelho está marcando 1,6 x 105 N/m². Sabendo que o organismo humano pode ser submetido, sem conseqüências danosas, a uma pressão de4 x 105 N/m², o mergulhador poderá descer, além do ponto em que se encontra, mais:Para resolver a questão, considere os seguintes dados:• massa específica da água = 1 g/cm³• pressão atmosférica = 105 N/m²• aceleração da gravidade = 10 m/s²a) 36 m b) 6 m c) 30 m d) 16 m e) 24 m

30. 4) U.F. Pelotas-RS A figura abaixo representa dois tubos abertos contendo líquidos diferentes. Uma mangueira interliga os dois, com uma torneira que permite entrada ou saída de ar. A, B, C e D são pontos das superfícies dos líquidos.Em relação às condições mostradas na figura, é correto afirmar que:a) a pressão no ponto B e maior que a atmosférica;b) os dois líquidos têm a mesma densidade;c) a pressão no ponto B e maior do que no ponto C;d) a pressão no ponto C e menor do que no ponto D;e) nos pontos A, B, C e D a pressão e a mesma5) UFPE O casco de um submarino suporta uma pressão externa de até 12,0 atm sem se romper. Se, por acidente, o submarino afundar no mar, a que profundidade, em metros, o casco se romperá? cosidere 1atm = 105N/m²a) 100 b) 110 c) 120 d) 130 e) 1406) PUC-PR A figura representa uma prensa hidráulica. Área da secção A = 1 m²Área da secção B = 0,25 m²Determine o módulo da força F aplicada no êmbolo A, para que o sistema esteja emequilíbrio.800 N d) 3200 N b) 1600 N e) 8000 N c) 200 N

31. Tabela de Prefixos.