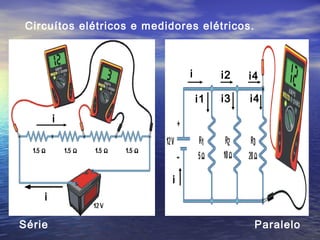
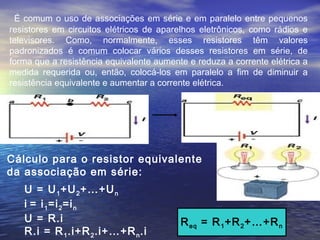
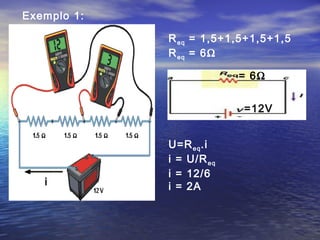
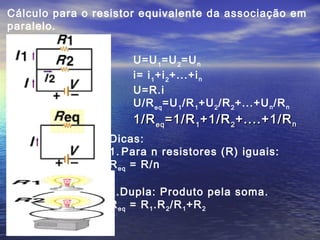
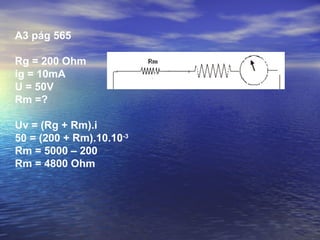
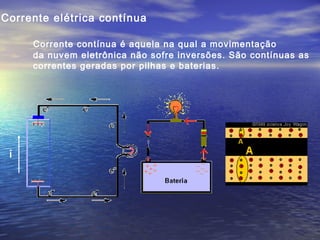
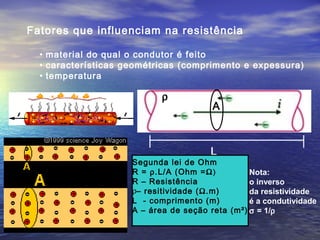
Este documento discute conceitos fundamentais de eletricidade como tensão elétrica, corrente elétrica, potência elétrica e resistência elétrica. Explica que a tensão elétrica é a razão entre o trabalho realizado sobre uma carga elétrica e a própria carga, e que está relacionada à energia fornecida a um aparelho. Também apresenta as leis de Ohm, que relacionam tensão, corrente e resistência em um circuito elétrico.

1. Tensão elétrica, d.d.p., força eletromotriz ou voltagem
A tensão associa-se a energia fornecida a um aparelho qualquer.
Uma carga, ao deslocar-se entre dois pontos no interior de um
condutor, sente a ação de uma força elétrica que realiza um
trabalho sobre essa carga ao deslocá-la. A razão entre esse
trabalho e a carga sobre a qual ele é realizado chama-se d.d.p.
(U = τ /q), tensão elétrica, força eletromotriz (f.e.m.) ou
voltagem. Essa voltagem é consequência do acúmulo de cargas
nos terminais metálicos da pilha ou bateria, que são
denominados de polos positivo e negativo através dos quais é
produzida uma tensão (d.d.p.) cujo valor vem impresso no corpo
desses geradores.
U
U = τ / q (J/C = V) SI
τ = U.q (J) SI

2. Aparelhos elétricos de uso cotidiano
relho tensão potência frequência outras
liquidificador 110/220V 350W 60Hz
chuveiro 220V 2800/7000W 60Hz
rádio 110/220V 6W 60Hz DC
6V
tv 110/220V 60W 60Hz
máquina de lavar 110/220V 60Hz
roupas
aspirador de pó 110/220V 850W 60Hz
computador 110V 60Hz
lâmpada 110/220V 100W 60Hz 1A
antena 300
Ohm

3. Movimento ordenado dos elétrons livres e sua relação com a
corrente elétrica.
Lâmpadas, ferros elétricos, computadores e eletrodomésticos em geral, só
funcionam quando ligados à fontes de energia (d.d.p.), tais como baterias
ou tomadas. Quando isso é feito se estabelece uma corrente elétrica no
interior desses aparelhos. Em um fio metálico desligado da fonte de
energia, a “nuvem” de elétrons livres move-se desordenadamente pela
rede cristalina. Tal movimento não constitui a corrente elétrica. Quando
ligamos o fio a uma fonte de energia, aparece uma força de natureza
elétrica que ordena o movimento dessa “nuvem”.

4. (1775 - 1836)
Intensidade de corrente elétrica (Ampère).
Quando ligamos o interruptor de uma lâmpada, o filamento metálico
no interior do bulbo fica sujeito a uma tensão elétrica (diferença de potencial)
que provoca um fluxo de carga elétrica, de maneira semelhante ao fluxo de
água numa mangueira, provocado por uma diferença de pressão. A
intensidade da corrente elétrica (i) está relacionada ao número de elétrons
livres (n) que são forçados a atravessar um volume infinitesimal imaginário
(A.∆L) transversal ao fio condutor, num determinado intervalo de tempo
(∆T).
A
∆L
i = n.e / ∆t = |Q| / ∆t (C/s = A)

5. Corrente elétrica alternada
Corrente alternada é aquela cujo sentido de movimentação
da nuvem eletrônica sofre inversões periodicamente.
No Brasil essa inversão ocorre com um frequência de 60
ciclos por segundo.
f = 60 ciclos/segundo = 60 Hertz = 60 Hz
i
1/120 1/60
t
ciclo

6. Corrente elétrica contínua
Corrente contínua é aquela na qual a movimentação
da nuvem eletrônica não sofre inversões. São contínuas as
correntes geradas por pilhas e baterias.
i

7. Relação entre as correntes elétricas num nó.
Nó é um ponto de um circuito elétrico onde mais
de dois fios condutores estão interliagados.
i1
i3 i1 + i2 = i3 + i4
i2 nó i4

8. Exemplo
1) Determinar a intensidade média de corrente elétrica no intervalo de tempo
de 0 a 4,0 s, conforme o gráfico abaixo. A área do gráfico (ixt) é
numericamente igual à variação de carga elétrica (∆Q).
∆Q = “área” (ixt) trapézio
∆Q = (B+b).h/2
∆Q = (4+2).10/2
∆Q = 30 C
i = ∆Q / ∆t = 30/4 = 7,5 A
2) A figura mostra 4 fios condutores interligados no ponto P. Em três desses
fios estão indicados os sentidos (sempre convencional) das correntes elétricas.
Qual a intensidade e o sentido da corrente i4? i1 = 20A, i2 =15A, i3 = 21A.
i2 i1 + i4 = i2 + i3
i1 i3 20 + i4 = 15 + 21
i4 = 16 A
i4

9. Energia elétrica nas residências e sua relação com o KWh
apresentado nas contas de luz.
E = Pot.∆t (W.h)
Aparelhos elétricos estão quase sempre efetuando transformações de
energia elétrica em outra forma de energia. Ao ligarmos um aparelho em
uma fonte de tensão qualquer, as cargas elétricas perdem energia elétrica
ao passar através dele. Essa energia não desaparece; ela é transferida
para o aparelho surgindo sob outra forma de energia, que dependerá do
tipo de aparelho utilizado. A energia elétrica consumida por um aparelho
ligado durante certo tempo é obtida através do produto da potência pelo
intervalo de tempo que o aparelho ficou ligado. Assim quanto maior a
potência de um aparelho, mais rapidamente fará girar o disco do relógio de
luz, que funciona como um tipo de motor, e mais KWh serão gastos em
comparação com o mesmo tempo de funcionamento de um aparelho de
menor potência.

10. Exemplos
1)Qual é o consumo de energia, durante um mês, em kWh, de
um chuveiro de 4000W, que é utilizado meia hora por dia?
E = kWh ? p/ ∆t = 30.0,5h = 15h E = 4.15
Pot = 4000W = 4kW E = 60 kWh
E = Pot.∆t (W.h)
2) Qual seria o valor da energia encontrada no exercício
anterior em Joule?
Pot = E /∆t ( J/s = W ) SI
E = 60 kWh E = 60000 J . 3600s
E = 60.1000 J.h s
s E = 216000000 J
E = 2,16.10 8

11. Em busca de uma relação entre potência (W), corrente (A)
e tensão (V).
Pot = E / ∆t (Watt =J/s) Pot = U.q / ∆t
W = U.q (Joule – J) Pot = U.i.∆t / ∆t
i = q / ∆t (Ampère = C/s = A) Pot = U.i
Pot = U.i (W) SI
A potência elétrica recebida por um aparelho será tanto maior quanto
maior a tensão à qual ele estiver submetido e quanto maior for a
orrente elétrica circulando. Uma mesma tensão de 12 V pode,
por exemplo, por em funcionamento uma lâmpada de 12 W ou um
motor de ignição de um automóvel de 2400 W. No entanto, no
primeiro caso teremos uma corrente de 1A, enquanto que no segundo
aso a corrente seria de 200 A. No primeiro caso, o farol ficaria aceso
por muitas horas, mas a bateria se descarregaria em poucos minutos
e o motor de partida fosse acionado muitas vezes com o automóvel
em combustível.

12. Exemplo:
m chuveiro submetido a uma tensão U = 220V opera com potência
ot = 4400W. A quantidade de água que passa pelo chuveiro em
ada segundo é igual a 44 g. Sendo o calor específico da água
=1cal/g°C e adotando 1cal = 4J, calcule:
) a intensidade de corrente no chuveiro;
) a energia consumida pelo chuveiro em 15min de funcionamento,
m J e kWh;
) a temperatura da água ao sair do chuveiro, sabendo que ela entra
ele a 20°C e supondo que toda energia elétrica dissipada seja
ntregue a água.
b) E = kWh, J? c) em cada segundo,
Pot = 4400W p/ ∆t = 15min = ¼ h passam 44 g de água
U = 220V E = Pot.∆t pelo chuveiro, que
m=44g/s E = 4400.¼ recebem 4400 J.
1cal = 4J E = 1100 Wh 1 cal_____4J
a) i= A? Q________4400J
E = 1,1 kWh Q = 1100 cal
Pot = U.i
m.c.∆t = 1100
i = Pot/U 1kWh______3600000 44.1.(t – 20) = 1100
i = 4400/220 1,1 kWh____ E t = 45°C
i = 20A E = 39,6.10 5 J

13. Condução elétrica em distintos materiais,
resistência elétrica e leis de Ohm.

14. Características dos materiais ditos: isolantes ou
condutores.
Condutor elétrico: é um corpo que possui grande quantidade de
portadores de carga elétrica facilmente movimentáveis, como:
Isolante elétrico: é um corpo que, ao contrário do condutor, não possui
quantidade significativa de portadores de carga elétrica facilmente
movimentáveis (vidro, plástico, mica, porcelana, seda etc.).

15. Resistência elétrica George S. Ohm
(1787-1854)
Físico alemão
Experimentalmente verificou-se que condutores de materiais distintos, quando
submetidos à mesma voltagem, são percorridos por correntes elétricas diferentes,
sendo que aqueles condutores que podem ser percorridos por correntes mais intensas
são, portanto, os de menor resistividade, ou seja, que apresentam menor resistência.
Primeira lei de Ohm
R = U/i (V / A = ohm = Ω)
U – d.d.p ( J/C = voltz =V)
i = corrente (C/s = ampère =A)
Curva característica do resistor ôhmico
U (V)
U = R.i
i (A)

16. Fatores que influenciam na resistência
• material do qual o condutor é feito
• características geométricas (comprimento e expessura)
• temperatura
ρ
A
L
Segunda lei de Ohm
R = ρ.L/A (Ohm =Ω) Nota:
R – Resistência o inverso
ρ– resitividade (Ω.m) da resistividade
L - comprimento (m) é a condutividade
A – área de seção reta (m²) σ = 1/ρ

17. Utilize a expressão da primeira lei de Ohm para demosntrar que
a potência elétrica pode também ser calculada por mais duas
expressões:
Pot = R.i² ou Pot = U²/R.
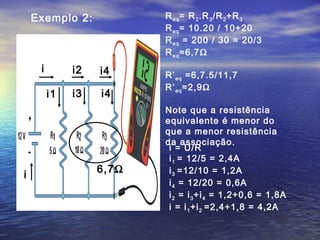
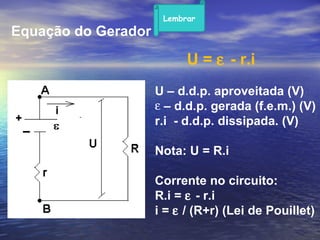
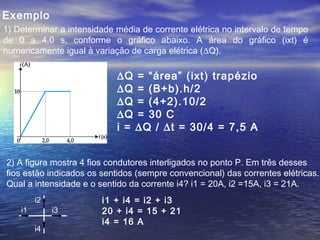
U = W/q (J/C = Volts = V) – tensão, d.d.p., voltagem.
Q = n.e (Coulomb-C) - carga elétrica.
Pot = E/∆t = U.i (J/s = Watt = W) – potência elétrica.
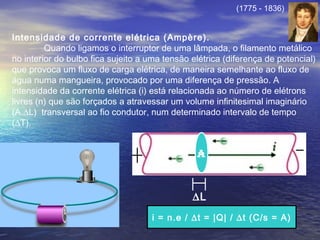
i =n.e/∆t = ∆Q/∆t (C/s = Ampère = A) – corrente elétrica.
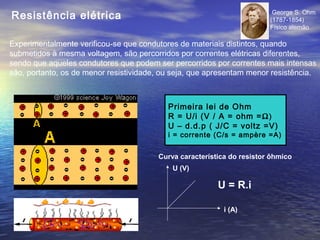
R = U/i (V/A = Ohm = Ω) – Resistência elétrica – 1 a lei de Ohm
Pot = U.i Pot = U.i
Pot = R.i.i Pot = U.U/R
Pot = R.i²
[W] = [Ω].[A]² Pot = U²/R
[J/s] = [V/A].[A]²
[J/s] = [J/C.A].[A ]²
[J/s] = [J.s/C²].[C/s]²
[J/s] = [J/s]

18. Ao ler a etiqueta de um aparelho elétrico, com as seguintes
especificações (100V – 40 Ω), Jéssica avaliou a potência do
aparelho como sendo de 250 W. Diga se Jéssica está certa.
Pot = U.i = U²/R = R.i²
U = 100 V
R = 40 Ω
Pot = 100² / 40
Pot = 250 W
Jéssica estava certa.

19. No projeto de instalação elétrica de uma casa foi utilizado um
fusível de 30 A para protegê-la. A voltagem da residência é 110 V.
Os moradores possuem os seguintes aparelhos eletrodomésticos:
Televisão – 150 W
Chuveiro – 2800 W
Lâmpadas – 60 W
Liquidificador – 250 W
Máquina de lavar roupas – 920 W
Determine quais aparelhos podem ser ligados simultaneamente.
Potência máxima que a rede aguenta:
i = 30 A
U = 110 V
Pot = U.i
Pot = 110.30 = 3300 W
Qualquer combinação que não ultrapasse
3300 W.

20. Exemplos
1) Determine a ddp que deve ser aplicada a um resistor de resistência 6
Ω para ser atravessado por uma corrente elétrica de 2A.
R = 6Ω U = r.i
i = 2 A U = 6.2
U = ? V U = 12 V
2) Um chuveiro elétrico é submetido a uma ddp de 220V, sendo percorrido
por uma corrente elétrica de 10A. Qual é a resistência elétrica do
chuveiro?
U = 220 V R = U/i
i = 10 A R = 220 / 10
R = Ω R = 22 Ω

21. 3) Um fio de cobre desencapado tem seção transversal de área A=6,0 mm²
e é percorrido por corrente de intensidade i=30A. O fio encontra-se a 35 0 C
e, nessa temperatura, a resistividade do cobre é ρ=1,8.10-5 Ω.mm.
Considere dois pontos M e N desse fio, separados por 1m. Calcule a
diferença de potencial entre os pontos M e N.
M A N
L
A = 6mm² U = ρ.L.i/A
i = 30 A U = 1,8.10 -5 .1000.30/6
ρ = 1,8.10 -5 Ω.mm U = 9.10 -2 V
L = 1 m = 1000 mm
U M,N = ? V
U = R.i
R = ρ.L/A

22. Circuítos elétricos e medidores elétricos.
i i2 i4
i1 i3 i4
i
i
i
Série Paralelo

23. É comum o uso de associações em série e em paralelo entre pequenos
resistores em circuitos elétricos de aparelhos eletrônicos, como rádios e
televisores. Como, normalmente, esses resistores têm valores
padronizados é comum colocar vários desses resistores em série, de
forma que a resistência equivalente aumente e reduza a corrente elétrica a
medida requerida ou, então, colocá-los em paralelo a fim de diminuir a
resistência equivalente e aumentar a corrente elétrica.
Cálculo para o resistor equivalente
da associação em série:
U = U 1 +U 2 +…+U n
i = i 1 =i 2 =i n
U = R.i R eq = R 1 +R 2 +…+R n
R.i = R 1 .i+R 2 .i+…+R n .i

24. Exemplo 1:
R eq = 1,5+1,5+1,5+1,5
R eq = 6Ω
= 6Ω
=12V
U=R eq .i
i = U/R eq
i = 12/6
i i = 2A

25. Cálculo para o resistor equivalente da associação em
paralelo.
U=U 1 =U 2 =U n
i= i 1 +i 2 +...+i n
U=R.i
U/R eq =U 1 /R 1 +U 2 /R 2 +...+U n /R n
1/R eq =1/R 1 +1/R 2 +....+1/R n
Dicas:
1. Para n resistores (R) iguais:
R eq = R/n
2.Dupla: Produto pela soma.
R eq = R 1 .R 2 /R 1 +R 2

26. Exemplo 2: R eq = R 2 .R 3 /R 2 +R 3
R eq = 10.20 / 10+20
R eq = 200 / 30 = 20/3
R eq ≈6,7Ω
i i2 i4 R’ eq =6,7.5/11,7
R’ eq ≈2,9Ω
i1 i3 i4
Note que a resistência
equivalente é menor do
que a menor resistência
da associação.
i = U/R
i 1 = 12/5 = 2,4A
6,7Ω i 3 =12/10 = 1,2A
i
i 4 = 12/20 = 0,6A
i 2 = i 3 +i 4 = 1,2+0,6 = 1,8A
i = i 1 +i 2 =2,4+1,8 = 4,2A

27. Exemplo 3: U = R eq .i
i = U/R eq
iB i = 3/5
i = 0,6 A
i ic
i U D = R.i
i
ic U D = 2.0,6 = 1,2V
U A = U D = 1,2V
i
U c = R B,C .i
U c = 1.0,6 = 0,6V
i = i B +i C
como R B =R C e
U B =U c temos:
i i B =i C =i/2 = 0,6/2
i
i B =i C = 0,3A

28. Curto-circuito
Dizemos que dois pontos estão em curto-circuito
quando existe um condutor ideal (R=0) conectado
entre eles. Nesse caso a d.d.p. entre esses dois pontos
é igual a zero.
x y
K
Caso o fio conectado entre os pontos x e y tenha
resistência nula, quando a chave K for fechada a
lâmpada C permanecerá apagada.

29. Exemplo 4:
Fuvest-SP Dispondo de pedaços de fios e 3
resistores de mesma resistência, foram montadas as
conexões apresentadas abaixo. Dentre essas,
aquela que apresenta a maior resistência elétrica
entre seus terminais é:
a) Req = R/3
b) Req = 0
c) Req = R +R/2 = 3R/2
d) Req = 2R.R/2R+R = 2R/3
e) Req=0

30. Exemplo 5:
Na montagem esquematizada na figura, temos três
resistores de resistências R1 = 100 Ohm, R2 = 30 Ohm,
R3 = 60 Ohm, um reostato R4 e um fio ideal F.
Determine a resistência equivalente entre os terminais
A e B, quando o reostato estiver ajustado em 80 Ohm.
A C
B B
A C

31. R1 = 100 Ohm; R2 = 30 Ohm
R3 = 60 Ohm; R4 = 80 Ohm
R 2,3 = 30.60/30+60 (Paralelo)
R 2,3 = 1800/90 = 20 Ω

32. R 4,3,2 = R 4 +R 2,3 (série)
R 4,3,2 = 80+20 = 100 Ω
R 1 = 100 Ω
R A,B = 100/2 = 50 Ω

33. “Geradores” de energia elétrica

34. Características do Gerador
Entre seus terminais existe uma d.d.p. conhecida
como força eletromotriz (f.e.m.).
Quando percorrido por uma corrente elétrica a d.d.p.
em seus terminais torna-se menor que a f.e.m., pois
há dissipação de energia na resistência interna do gerador.

35. Equação do Gerador
U = ε - r.i
U – d.d.p. aproveitada (V)
ε – d.d.p. gerada (f.e.m.) (V)
r.i - d.d.p. dissipada. (V)
Nota: U = R.i
Corrente no circuito:
R.i = ε - r.i
i = ε / (R+r) (Lei de Pouillet)

36. Curva característica do gerador e
corrente de curto-circuito (icc)
U = ε - r.i
R.i = ε - r.i
0.i = ε - r.i
icc = ε / r

37. Gerador em circuito aberto
U = ε - r.i
U = ε - r.0
U=ε

38. Potências (W) elétricas no gerador
Potência útil : Potu = U.i
Potência perdida: Potd = r.i²
Potência total: Pott = Potu + Potd
Pott = U.i + r.i²
Pott = (ε – r.i).i + r.i²
Pott = ε .i
Rendimento: η = Potu / Pott = U / ε

39. Nota:
Máxima transferência de potência
Potu = U.i = (ε – r.i).i
Potu = ε.i – r.i² (equação do 2° grau)
Note que:
Para o gerador em circuito aberto (i=0) – Potu = 0
Para o gerador em curto-circuito (i = icc = ε / r ) – Potu = 0

40. Corrente para Potumáx : i = icc / 2; icc = ε / r
i = ε / 2r
D.D.P. para Potumáx : U = ε – r.i = ε – r.ε /2r
U=ε /2
Resistência (R) ligada ao gerador para Potumáx :
U = ε – r.i
R.i = ε – r.i
i = ε / (R + r)
ε/ 2r = ε / (R + r)
R + r = 2r
R=r
Rendimento para Potumáx:
η= U / ε = ε / 2.ε
η = 0,5
Note que, para máxima transferência de potência, o gerador tem um rendimento
de 50%.

41. Associação de geradores:

42. Associação de geradores:

43. Receptores de energia elétrica

44. Lembrar
Equação do Gerador
U = ε - r.i
U – d.d.p. aproveitada (V)
ε – d.d.p. gerada (f.e.m.) (V)
r.i - d.d.p. dissipada. (V)
Nota: U = R.i
Corrente no circuito:
R.i = ε - r.i
i = ε / (R+r) (Lei de Pouillet)

45. Características do Receptor
Entre seus terminais existe uma d.d.p. conhecida
como força contra eletromotriz (f.c.e.m.).
Quando percorrido por uma corrente elétrica a d.d.p.
em seus terminais é maior que a f.c.e.m., pois
há dissipação de energia na resistência interna do receptor.

46. Equação do Receptor
U = ε× + r´.i
U – d.d.p. que chega (V)
ε´ – d.d.p. aproveitada (f.c.e.m.) (V)
r´.i - d.d.p. dissipada. (V)
Nota: U = ε - r.i
Corrente no circuito:
ε – r.i = ε× + r´.i
i = (ε – ε×) / (r´+ r)
Note que a corrente elétrica (i) tem sentido (-) para (+) no interior do
gerador, e de (+) para (-) no interior do receptor.

47. Curva característica do receptor
Note que quando U
aumenta i também
aumenta, e que quando
i = 0 U = ε×.

48. Leis de Kirchhoff
 A lei de Pouillet permite determinar a intensidade
de corrente num circuito simples. Quando o
circuito não pode ser reduzido a um circuito (1824 – 1887)
simples, para a determinação de todas as
intensidades de corrente elétrica recorre-se às
chamadas leis de Kirchhoff: lei dos nós e lei das
malhas.
 A lei dos nós e a lei das malhas
são utilizadas para determinar
a distribuição da corrente nos
circuitos elétricos.

49. Considere uma rede elétrica constituída de dois geradores, (E1, r1) e (E2, r2), de um
receptor, (E3, r3), e de resistores de resistências elétricas, R1, R2 e R3.
Numa rede elétrica chama-se nó o ponto no qual a corrente elétrica se divide. No
exemplo dado, B e E são nós. Os trechos de circuito entre dois nós consecutivos são
denominados ramos. Na rede elétrica dada, os ramos são três:
BAFE, BE e BCDE.
Qualquer conjunto de ramos formando um percurso fechado recebe o nome de malha.
No circuito em questão as malhas são: ABEFA, BCDEB e ABCDEFA.

50. A cada ramo do circuito atribuímos um sentido de corrente elétrica. Esse sentido,
embora arbitrário, deve ser coerente com o elemento de circuito do ramo. Sendo
gerador, a corrente entra pelo terminal negativo e, sendo receptor, pelo positivo.
Primeira lei
i3 = i2 + i1

51. Segunda Lei
VA – R1.i1 + r2.i2 – E2 - R2.i1 + E1 – r1.i1 = VA
-R1.i1 + r2.i2 – E2 - R2.i1 + E1 – r1.i1 = 0

52. Energia elétrica e Potência elétrica
E = Pot.∆t (W.h)
Energia elétrica nas residências e sua relação com o KWh apresentado
nas contas de luz.
Aparelhos elétricos estão quase sempre efetuando transformações de
energia elétrica em outra forma de energia. Ao ligarmos um aparelho em
uma fonte de tensão qualquer, as cargas elétricas perdem energia elétrica
ao passar através dele. Essa energia não desaparece; ela é transferida
para o aparelho surgindo sob outra forma de energia, que dependerá do
tipo de aparelho utilizado. A energia elétrica consumida por um aparelho
ligado durante certo tempo é obtida através do produto da potência pelo
intervalo de tempo que o aparelho ficou ligado. Assim quanto maior a
potência de um aparelho, mais rapidamente fará girar o disco do relógio de
luz, que funciona como um tipo de motor, e mais KWh serão gastos em
comparação com o mesmo tempo de funcionamento de um aparelho de
menor potência.

53. Exemplos
1)Qual é o consumo de energia, durante um mês, em kWh, de
um chuveiro de 4000W, que é utilizado meia hora por dia?
E = kWh ? p/ ∆t = 30.0,5h = 15h E = 4.15
Pot = 4000W = 4kW E = 60 kWh
E = Pot.∆t (W.h)
2) Qual seria o valor da energia encontrada no exercício
anterior em Joule?
Pot = E /∆t ( J/s = W ) SI
E = 60 kWh E = 60000 J . 3600s
E = 60.1000 J.h s
s E = 216000000 J Nota:
E = 2,16.10 8 J 1kWh = 3,6.10 6 J

54. Em busca de uma relação entre potência (W), corrente (A)
e tensão (V).
Pot = E / ∆t (Watt =J/s) Pot = U.q / ∆t
W = U.q (Joule – J) Pot = U.i.∆t / ∆t
i = q / ∆t (Ampère = C/s = A) Pot = U.i
Pot = U.i (W) SI
A potência elétrica recebida por um aparelho será tanto maior quanto
maior a tensão à qual ele estiver submetido e quanto maior for a
orrente elétrica circulando. Uma mesma tensão de 12 V pode,
por exemplo, por em funcionamento uma lâmpada de 12 W ou um
motor de ignição de um automóvel de 2400 W. No entanto, no
primeiro caso teremos uma corrente de 1A, enquanto que no segundo
aso a corrente seria de 200 A. No primeiro caso, o farol ficaria aceso
por muitas horas, mas a bateria se descarregaria em poucos minutos
e o motor de partida fosse acionado muitas vezes com o automóvel
em combustível.
Nota: Pot = U.i e U = R.i
Pot = R.i² = U²/R

55. Potências (W) elétricas no receptor
Potência útil : Potu = ε× .i
Potência perdida: Potd = r´.i²
Potência total: Pott = Potu + Potd
Pott = ε×.i + r´.i²
Pott = (ε× + r´.i).i
Pott = U.i
Rendimento: η = Potu / Pott = ε×/U

56. Potências (W) elétricas no gerador
Potência útil : Potu = U.i
Potência perdida: Potd = r.i²
Potência total: Pott = Potu + Potd
Pott = U.i + r.i²
Pott = (ε – r.i).i + r.i²
Pott = ε .i
Rendimento: η = Potu / Pott = U / ε

57. Síntese gerador - receptor

58. Medidores elétricos:
Amperímetro ideal: (Não tem resistência interna)
- é ligado em série em determinado ramo do circuito.
- mede a intensidade da corrente elétrica (i – A)
Voltímetro ideal: (Possui uma resistência interna extremamente alta)
- é ligado em paralelo em determinado ramo do circuito
- mede d.d.p (U – V)

59. Galvanômetro
Utilizando um galvanômetro
para medir correntes e tensões elétricas.
– Interação entre a corrente elétrica em uma bobina e
um campo magnético
– Constrói-se um circuíto simples de forma que a
corrente elétrica que passa pelo galvanômetro seja
proporcional à corrente ou tensão elétrica que
queremos medir
– Ajusta-se uma escala de fundo de modo a converter
a corrente no galvanômetro para a grandeza medida.

60. Utilizando um galvanômetro para medir
corrente elétrica.
• Se a corrente no
circuito for menor do
aquela que o
galvanômetro
suporta, basta
conectá-lo ao circuito
• E se for maior
– Desvia-se parte da UG = Us
corrente para um
resistor em paralelo RG.i1 = Rs.i2
(Rs)

61. O Amperímetro
• Um galvanômetro
acoplado a vários
resistores em
paralelo
– A escolha do
resistor determina
o fundo de escala
(corrente máxima)
que pode ser
medida.

62. Utilizando um galvanômetro
para medir tensão elétrica
Desvia-se parte da corrente do
circuíto para o galvanômetro
(U = Ri)
Para medir tensões que desviem
correntes acima do limite do
galvanômetro, aumenta-se a
resistência de modo a limitar
a corrente desviada
i s = ig
Us = Ug
Rs Rg

63. O Voltímetro
Um galvanômetro
acoplado a vários
resistores em série.
– A escolha do
resistor determina
o fundo de escala
(tensão elétrica
máxima) que pode
ser medida.
– O instrumento faz
a conta (U = Ri)
automaticamente

64. Na prática
• Utiliza-se um voltímetro para medir a
tensão no resistor
• E um amperímetro para medir a corrente
no resistor

65. Uma consequência importante
• Voltímetros e amperímetros possuem
resistência
• Voltímetros e amperímetros funcionam
através do desvio de um pouco de
corrente para o instrumento
• Voltímetros e amperímetros
MODIFICAM as tensões e
correntes em um circuito. Eles
alteram as medidas

66. Quais as leituras do amperímetro e do voltímetro no circuito abaixo?
Req = 2+3+4+1 = 10 Ω
U = R.i
50 = 10.i
i = 5A
No ramo do voltímetro temos:
Req = 4+3 = 7Ω
U = R.i
U = 7.5 = 35V

67. Ponte de Wheatstone
• É uma associação de
três resistores fixos e
um variável (reostato).
• Serve para determinar
a resistência de um resistor. UA,B = UA,D
• Varia-se a resistência do r1.i1 = r3.i2 (I)
reostato de forma que a
intensidade da corrente no UB,C = UD,C
galvanômetro seja zero, r2.i1 = r4.i2 (II)
assim, UB,D = 0 (ponte em
equilíbrio). (I) : (II)
r1 = r3
r2 r4
r1.r4 = r3.r2

68. Ponte de fio
R = ρ.L / A
R / L = ρ / A (constante) r3.L4 = r2.L3

69. A7
i = i’+ i’’
Malha no Amperímetro
(sentido horário):
-12i’ + 20i’’ = 0
i’’ = 0,6 i’ (I)
Malha na associação esquerda (sentido ah):
-12i’ – 15i’ – 5(i’+ i’’) +10 = 0
32i’ + 5i’’ = 10 (II)
32i’ + 3i’ = 10 (I) e (II)
i’ = 10 /35 A
i’’ = 6/35 A
i = 16/35 A Ou Ponte em eq.:
Malha na associação direita 12.(x+5) = 20.15
(sentido h)
-20.6/35 – 5.6/35 – 6x/35 – 5.16/35 + 10 = 0 12x + 60 = 300
x = 20 Ohm
x = 20 Ohm

70. A1 pág 565
Rg = 20 Ohm
ig = 0,1 A
Rs =?
i = 10 A
Ug = Us
Rg.ig = Rs.is
i = i s + ig
is = 10 – 0,1 = 9,9 A
20.0,1 = Rs.9,9
Rs ≈ 0,2 Ohm

71. A2 pág 565
Ra = 0,20 Ohm = (Req)
iantes = 1,0 mA
idepois = 5,0 mA
Rs = ?
Ua = Ra.iantes
Ua = 0,2mV
Ua = Req.idepois
0,2m = Ra.Rs . idepois
Ra+Rs
0,2m.(0,2+Rs) = 0,2.Rs.5m
0,04 + 0,2Rs = Rs
0,8Rs = 0,04

72. A3 pág 565
Rg = 200 Ohm
ig = 10mA
U = 50V
Rm =?
Uv = (Rg + Rm).i
50 = (200 + Rm).10.10-3
Rm = 5000 – 200
Rm = 4800 Ohm

73. A4 pág 567
Ponte em equilíbrio: UB,D = 0
8.R = 20.3
R = 7,5 Ohm
A5
Ponte em equilíbrio: iA = 0
(4+1).Rx = (4+4).10
Rx = 16 Ohm
A6
a) Ponte em equilíbrio:
i =0
b) Req = 3,5.7 / 10,5
Req ≈ 2,3 Ohm