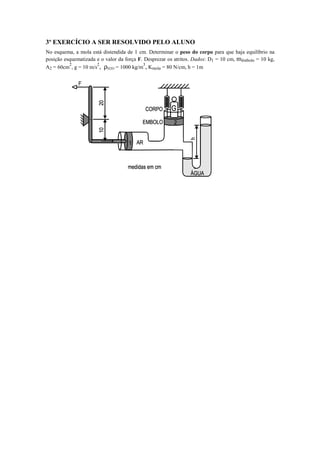
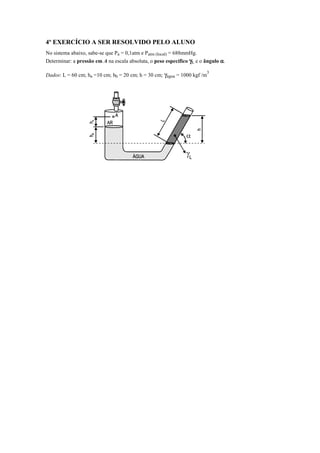
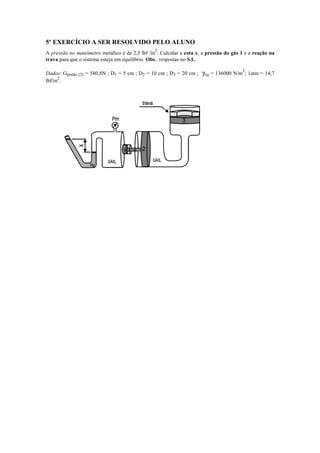
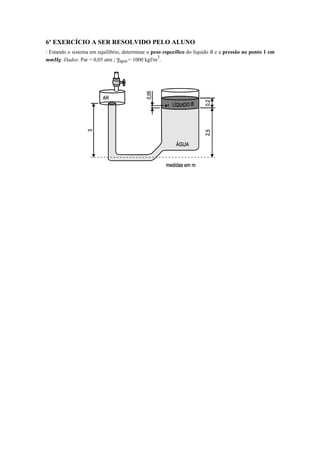
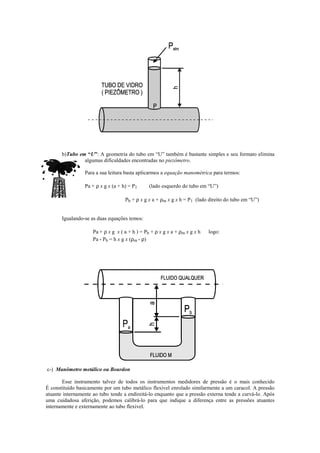
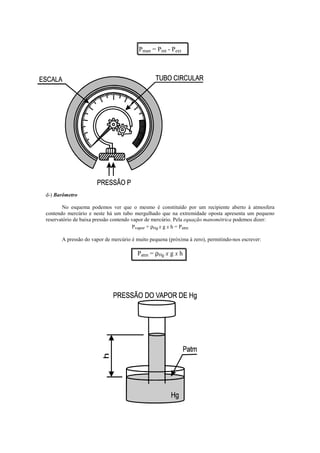
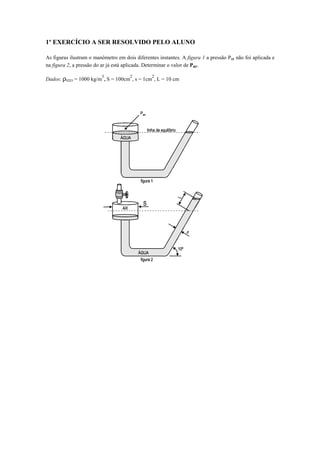
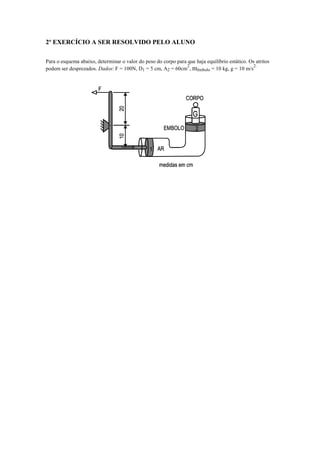
O documento apresenta os principais conceitos e equações relacionados à manometria, incluindo: 1) A equação manométrica que permite calcular diferenças de pressão em colunas de fluidos; 2) As escalas de pressão absoluta e efetiva; 3) Diferentes tipos de medidores de pressão como piezômetro, tubo em U e manômetro.

1. Módulo 3: Conteúdo programático – Manometria
Bibliografia: Bunetti, F. Mecânica dos Fluidos , São Paulo, Prentice Hall, 2007.
Equação Manométrica
A aplicação da lei de Stevin e de Pascal, de uma forma mais rápida, mais prática é chamada de
Equação Manométrica.
Para o esquema abaixo, determine a diferença de pressão Pa - Pb = ?
Para resolvermos esse problema, tendo em vista que temos três diferentes colunas com três
fluidos, temos que aplicar a Lei de Stevin três vezes, determinar três constantes de integração. Mas já
sabemos que o valor da constante de integração é o valor da pressão na origem do eixo “y” que estamos
analisando. Logo o valor de C, para “y”, é Pa, o valor C2 é P1, o valor de C3 é Pb.
Aplicando-se a cada um dos fluidos a equação geral já deduzida
P = ρ.g .y + C temos:
P1 = ρ1. g . h1 + Pa {A}
P2 = ρ2. g . h2 + P1 (lado esquerdo) {B}
P3 = ρ3. g . h3 + Pb (lado direito) {C}
Vamos substituir a equação {C} em {B} ficando:
ρ3. g . h3 + Pb = ρ2. g . h2 + P1 {D}
Vamos substituir a equação {A} em {D}:
ρ3. g . h3 + Pb = ρ2. g . h2 + ρ1. g . h1 + Pa
logo, resolvendo temos:
Pa - Pb = ρ3. g . h3 - (ρ2. g . h2 + ρ1. g . h1) {I}
Observe que poderíamos chegar ao mesmo resultado utilizando a equação manométrica. Para isso basta
escolhermos um dos extremos que chamaremos de extremo inicial e vamos nos dirigir ao outro extremo
que chamaremos de extremo final. Ao partirmos do extremo inicial e nos dirigirmos ao final, sempre que
descermos num fluido escreveremos )( ghρ+ e sempre que subirmos escreveremos )( ghρ− , sendo h
medido sempre verticalmente.

2. ESCALAS DE PRESSÃO
Para física a pressão de significado físico é a pressão absoluta, Porém muitas vezes essa escala
dificulta a solução dos problemas. Criou-se então o conceito de pressão efetiva ou relativa, isto é, uma
escala que adota uma outra referência (referência à pressão atmosférica local), fato esse que não conduz a
diferentes resultados, pois uma diferença de pressão avaliada na escala absoluta é a mesma de uma
diferença de pressão avaliada na escala efetiva.
Escala Efetiva ou Relativa Escala Absoluta
pressão efetiva pressão absoluta
0(zero) pressão atmosférica local
-pressão atmosférica local vácuo absoluto
A mudança de escala se faz pela seguinte expressão:
Pabs = Pefe + Patm local
Para não deixar dúvida sempre que utilizarmos a escala absoluta das pressões, devemos deixar
isso de forma bem clara, isto é, devemos após a unidade colocarmos o índice abs.
Exemplos: Pa (abs); kgf/cm
2
(abs).
MEDIDORES DE PRESSÃO
Vários são os medidores de pressão, porém todos eles obedecem as duas leis fundamentais da
Estática dos Fluidos que são as já mencionadas LEIS DE PASCAL e LEI DE STEVIN. Dentre os
principais tipos destacam-se:
a-) Piezômetro Instrumento muito simples, consistindo de um tubo vertical de vidro ou qualquer outro
material transparente. Basta medirmos a cota h e conhecermos a massa específica do
fluido gerador da cota h para que possamos aplicar a LEI DE STEVIN e obtermos a
pressão P. Podemos aplicar a equação manométrica para chegarmos ao seguinte
equacionamento:
Patm + ρ x g x h = Ptubo

3. b)Tubo em “U”: A geometria do tubo em “U” também é bastante simples e seu formato elimina
algumas dificuldades encontradas no piezômetro.
Para a sua leitura basta aplicarmos a equação manométrica para termos:
Pa + ρ x g x (a + h) = P1 (lado esquerdo do tubo em “U”)
Pb + ρ x g x a + ρm x g x h = P1 (lado direito do tubo em “U”)
Igualando-se as duas equações temos:
Pa + ρ x g x ( a + h ) = Pb + ρ x g x a + ρm x g x h logo:
Pa - Pb = h x g x (ρm - ρ)
c-) Manômetro metálico ou Bourdon
Esse instrumento talvez de todos os instrumentos medidores de pressão é o mais conhecido
É constituído basicamente por um tubo metálico flexível enrolado similarmente a um caracol. A pressão
atuante internamente ao tubo tende a endireitá-lo enquanto que a pressão externa tende a curvá-lo. Após
uma cuidadosa aferição, podemos calibrá-lo para que indique a diferença entre as pressões atuantes
internamente e externamente ao tubo flexível.

4. Pman = Pint - Pext
d-) Barômetro
No esquema podemos ver que o mesmo é constituído por um recipiente aberto à atmosfera
contendo mercúrio e neste há um tubo mergulhado que na extremidade oposta apresenta um pequeno
reservatório de baixa pressão contendo vapor de mercúrio. Pela equação manométrica podemos dizer:
Pvapor + ρHg x g x h = Patm
A pressão do vapor de mercúrio é muito pequena (próxima à zero), permitindo-nos escrever:
Patm = ρHg x g x h

5. 1º EXERCÍCIO RESOLVIDO
A figura ilustra uma situação de equilíbrio estático, sem atrito. Determinar o valor da força F.
Dados: A1 = 50cm
2
, A2 = 20cm
2
, Pman = 2 atm , ρH2O = 1000 kg/m
3
, ρHg = 13600 kg/m
3
, g = 10m/s
2
Solução:
atmarman PPP −= adotando escala efetiva de pressão 0=atmP
Logo: PaatmPP arman
5
10.22 ===
Analisando as força do pistão:
FAAPAP agar +−= )( 211 eq.1
Pela eq. Manométrica
hghgatmagagag ghPghP ρρ +=+
Da eq. manométrica resulta
²
116000
m
N
Pag =
Da eq 1 resulta:
F=652 N
agua

6. 2º EXERCÍCIO RESOLVIDO
A figura ilustra uma situação de equilíbrio estático, sem atrito. Determinar o valor da cota h.
Dados: A1 = 50cm
2
, A2 = 20cm
2
, A3 = 30cm
2
, Pman1 = 1,5 kgf/cm
2
, Pman2 = 2 atm,
Par2 = 5x10
5
N/m
2
, ρH2O = 1000 kg/m
3
, ρHg = 13600 kg/m
3
, g = 10m/s
2
Solução: atmarman PPP −= 11 adotando escala efetiva de pressão 0=atmP Logo:
PaatmPP arman
5
1 10.5,15,1 ===
Analisando as força do pistão: 332123211 )()( APAAPAAPAP aragarar +−=−+ eq.1
Pela eq. Manométrica: hghgaragagag ghPghP ρρ +=+ 2
Da eq. Manométrica resulta : hghgarar ghPP ρ+= 32

7. 1º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
As figuras ilustram o manômetro em dois diferentes instantes. A figura 1 a pressão Par não foi aplicada e
na figura 2, a pressão do ar já está aplicada. Determinar o valor de Par.
Dados: ρH2O = 1000 kg/m
3
, S = 100cm
2
, s = 1cm
2
, L = 10 cm

8. 2º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
Para o esquema abaixo, determinar o valor do peso do corpo para que haja equilíbrio estático. Os atritos
podem ser desprezados. Dados: F = 100N, D1 = 5 cm, A2 = 60cm
2
, mêmbolo = 10 kg, g = 10 m/s
2.

9. 3º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
No esquema, a mola está distendida de 1 cm. Determinar o peso do corpo para que haja equilíbrio na
posição esquematizada e o valor da força F. Desprezar os atritos. Dados: D1 = 10 cm, mêmbolo = 10 kg,
A2 = 60cm
2
, g = 10 m/s
2
, ρH2O = 1000 kg/m
3
, Kmola = 80 N/cm, h = 1m

10. 4º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
No sistema abaixo, sabe-se que Pa = 0,1atm e Patm (local) = 688mmHg.
Determinar: a pressão em A na escala absoluta, o peso específico γγγγL e o ângulo αααα.
Dados: L = 60 cm; ha =10 cm; hb = 20 cm; h = 30 cm; γágua = 1000 kgf /m
3

11. 5º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
A pressão no manômetro metálico é de 2,5 lbf /in
2
. Calcular a cota x, a pressão do gás 1 e a reação na
trava para que o sistema esteja em equilíbrio. Obs.: respostas no S.I..
Dados: Gpistão (3) = 580,8N ; D1 = 5 cm ; D2 = 10 cm ; D3 = 20 cm ; γHg = 136000 N/m
3
; 1atm = 14,7
lbf/in
2
.

12. 6º EXERCÍCIO A SER RESOLVIDO PELO ALUNO
: Estando o sistema em equilíbrio, determinar o peso específico do líquido B e a pressão no ponto 1 em
mmHg. Dados: Par = 0,05 atm ; γágua = 1000 kgf/m
3
.