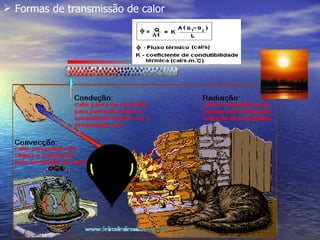
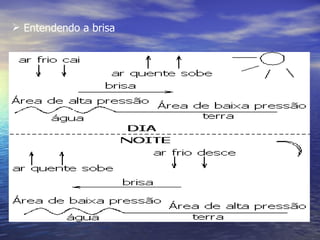
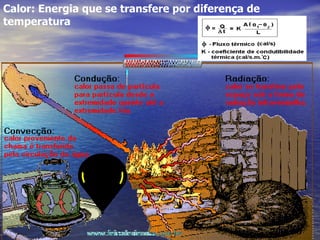
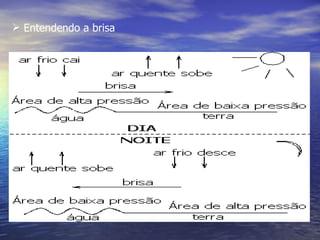
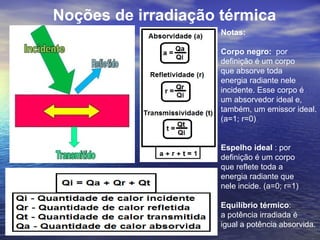
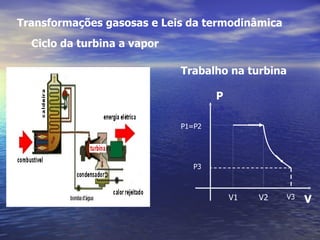
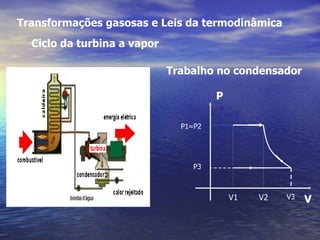
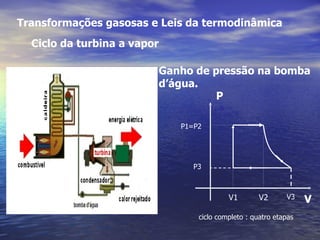
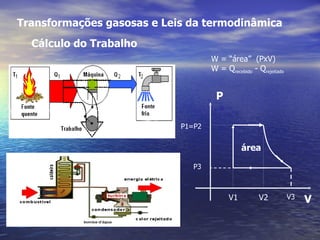
1) O documento discute termos como calor, temperatura e formas de transmissão de calor. Explica que calor é energia térmica que flui da região mais quente para a mais fria e que temperatura mede o nível de agitação térmica e indica o fluxo de calor.
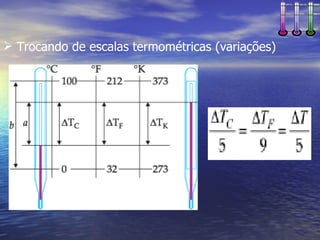
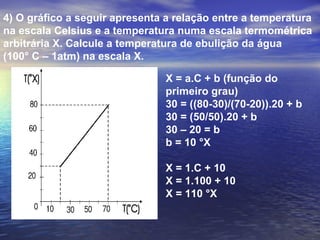
2) Apresenta diferentes escalas termométricas como Celsius, Fahrenheit e Kelvin e discute como converter entre elas.
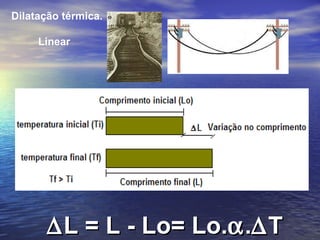
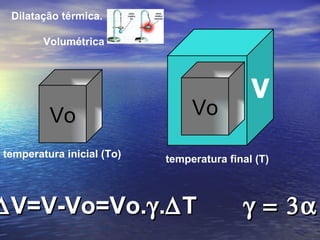
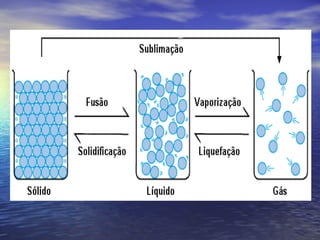
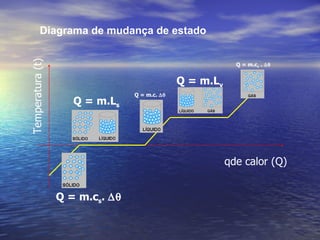
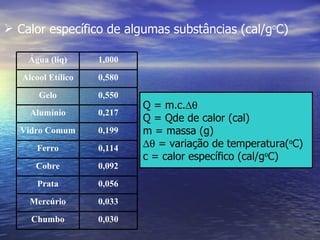
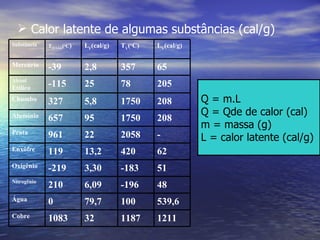
3) Aborda conceitos como calor sensível, calor latente, capacidade térmica e dilatação térmica, importantes para