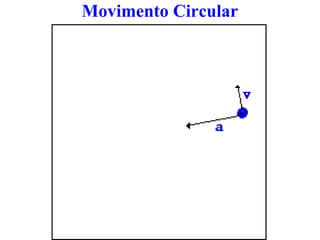
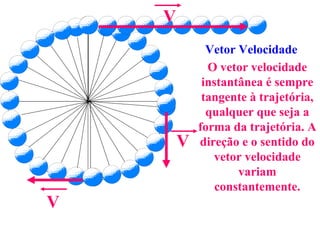
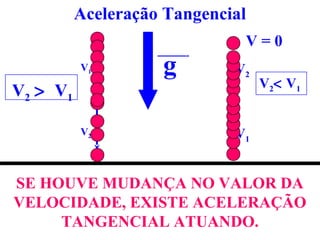
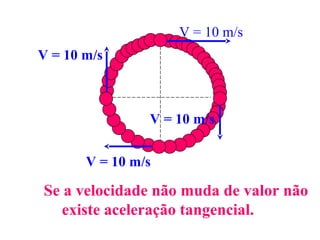
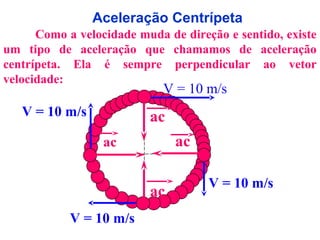
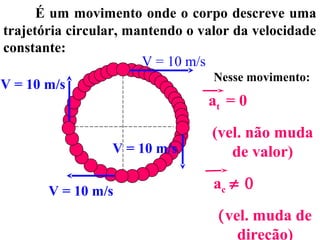
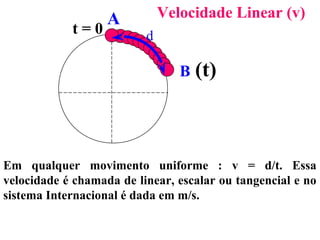
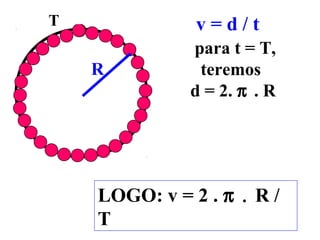
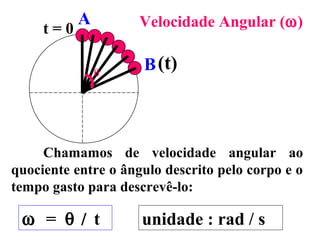
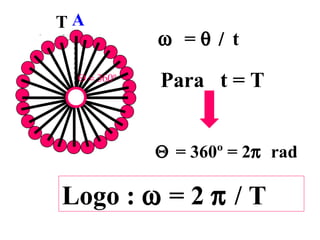
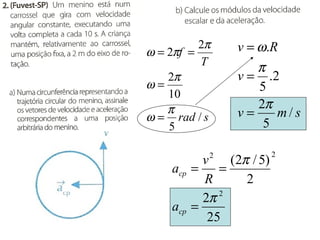
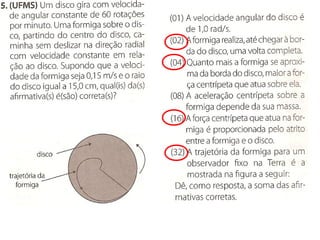
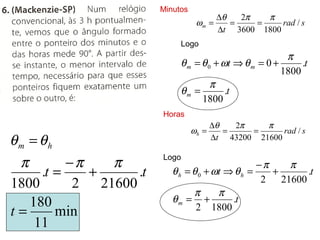
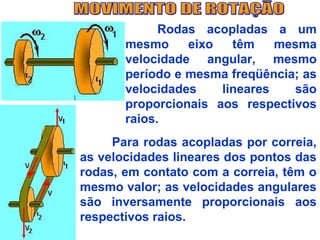
1) O documento discute conceitos de movimento circular como velocidade angular, velocidade linear, aceleração centrípeta e tangencial. 2) Rodes acoplados a um mesmo eixo têm mesma velocidade angular e frequência, enquanto suas velocidades lineares são proporcionais aos seus raios. 3) Para rodas acopladas por correia, as velocidades lineares em contato com a correia são iguais, e as velocidades angulares são inversamente proporcionais aos raios.

1. Profº Anderson LESSA

2. Movimento Circular

3. V
Vetor Velocidade
O vetor velocidade
instantânea é sempre
tangente à trajetória,
qualquer que seja a
forma da trajetória. A
V direção e o sentido do
vetor velocidade
variam
constantemente.
V

4. Se aceleração é a grandeza que mede
mudança na velocidade e se existem duas maneiras
independentes da velocidade mudar, existem dois
tipos de aceleração.
Existe uma aceleração que muda o valor da
velocidade. Ela é chamada de aceleração
tangencial. A aceleração que muda a direção e
sentido da velocidade é a aceleração centrípeta.

5. Aceleração Tangencial
V=0
V1 g V2
V2< V1
V2 > V1
V2 V1
SE HOUVE MUDANÇA NO VALOR DA
VELOCIDADE, EXISTE ACELERAÇÃO
TANGENCIAL ATUANDO.

6. ACELERAÇÃO TANGENCIAL:
Quando a velocidade muda de
valor existe aceleração tangencial.
No movimento acelerado, ela tem o
mesmo sentido da velocidade; no
movimento retardado, tem sentido
contrário.

7. V = 10 m/s
V = 10 m/s
V = 10 m/s
V = 10 m/s
Se a velocidade não muda de valor não
existe aceleração tangencial.

8. Aceleração Centrípeta
Como a velocidade muda de direção e sentido, existe
um tipo de aceleração que chamamos de aceleração
centrípeta. Ela é sempre perpendicular ao vetor
velocidade:
V = 10 m/s
V = 10 m/s ac
ac ac
V = 10 m/s
ac
V = 10 m/s

10. É um movimento onde o corpo descreve uma
trajetória circular, mantendo o valor da velocidade
constante:
V = 10 m/s
Nesse movimento:
V = 10 m/s
at = 0
(vel. não muda
V = 10 m/s de valor)
V = 10 m/s ac ≠ 0
(vel. muda de
direção)

12. T t=0 PERÍODO (T)
O PERÍODO DO MCU É O TEMPO GASTO
PARA DAR UMA VOLTA COMPLETA. SUA
UNIDADE É O SEGUNDO(S).

13. f t 1s0
= FREQUÊNCIA (f)
A FREQUÊNCIA É O Nº DE VOLTAS DADAS
DADAS POR UNIDADE DE TEMPO. A FREQUÊNCIA
É O INVERSO DO PERÍODO. SUA UNIDADE É O
HERTZ (Hz).

14. A Velocidade Linear (v)
t=0 d
B (t)
Em qualquer movimento uniforme : v = d/t. Essa
velocidade é chamada de linear, escalar ou tangencial e no
sistema Internacional é dada em m/s.

15. T t=0 v=d/t
para t = T,
R teremos
d = 2. π . R
LOGO: v = 2 . π . R /
T

16. A Velocidade Angular (ω)
t=0
θ
B (t)
Chamamos de velocidade angular ao
quociente entre o ângulo descrito pelo corpo e o
tempo gasto para descrevê-lo:
ω = θ / t unidade : rad / s

17. TA
t=0
ω =θ / t
Θ = 360º
Para t = T
Θ = 360º = 2π rad
Logo : ω = 2 π / T

18. Podemos também expressar a
velocidade linear e a velocidade angular em
função da freqüência. Sabemos que:
T=1/f
2.π .
v=2.π . R/T= =2.π .R.f
R1/ f
2.π
ω = 2. π / T = =2.π .f
1/f

19. V = 10 m/s
V = 10 m/s ac Aceleração
ac ac Centrípeta
V = 10 m/s
ac
V = 10 m/s
O valor da aceleração centrípeta será
dado por:
a c = V2 / R

21. Rodas acopladas a um
mesmo eixo têm mesma
velocidade angular, mesmo
período e mesma freqüência; as
velocidades lineares são
proporcionais aos respectivos
raios.
Para rodas acopladas por correia,
as velocidades lineares dos pontos das
rodas, em contato com a correia, têm o
mesmo valor; as velocidades angulares
são inversamente proporcionais aos
respectivos raios.

22. VA = VB
fB < f A
TA < TB
WA > WB
Observe que ambas
giraram juntas em v1 = v2
sentidos opostos, ω .R = ω R
1 1 2 2
sendo assim:
2π . f1.R1 = 2π . f 2 .R2
f1.R1 = f 2 .R2

23. Exercícios (p.24)
c) 1 / 6 − 2s
2π π
a) ω= = rad / s
12 6 1 − ∆t
∆t = 12 s
b) v = ωR
π
v = .6
6
v =π m/s

24. 2π v = ω.R
ω = 2πf =
T
π
2π v = .2
ω= 5
10
π 2π
ω = rad / s v= m/s
5 5
(2π / 5)
2 2
v
acp = =
R 2
2π 2
acp =
25

25. π
v = ω.R = .6400km
12h
1600π
v= km / h
3
∆θ 2π 2π
ω= = =
∆t 24h 86400 s
π
ω= rad / s
43200

26. v1 = v2
f1.R1 = f 2 .R2
150.20 = f 2 .100
f 2 = 30rpm

28. Minutos
∆θ 2π π
ωm = = = rad / s
∆t 3600 1800
Logo
π
θ m = θ 0 + ωt ⇒ θ m = 0 + .t
1800
π
θm = .t
1800
Horas
∆θ 2π π
ωh = = = rad / s
θm = θh ∆t 43200 21600
π −π π Logo
−π π
.t = + .t θ h = θ 0 + ωt ⇒ θ h = +
2 21600
.t
1800 2 21600
π π
180 θm = + .t
t= min 2 1800
11