1) O documento apresenta uma lista de exercícios de matemática com 40 questões sobre conjuntos, funções e domínios. 2) As questões abordam tópicos como operações com conjuntos, produto cartesiano, gráficos de funções, equações funcionais e determinação de domínios. 3) A lista tem o objetivo de avaliar o conhecimento dos estudantes em diferentes conceitos fundamentais de álgebra.

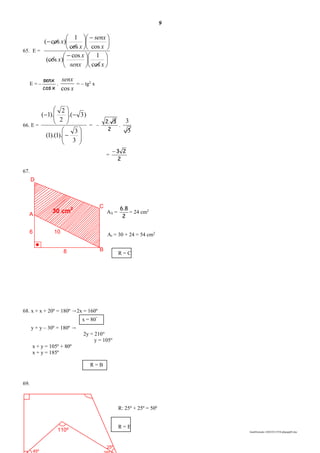
1. MATEMÁTICA
Professores Arthur, Denilton, Elizeu e Rodrigo
LISTA DE EXERCÍCIOS 03 – 2a
UNIDADE
01. (UCSal-BA) Dados os conjuntos A = {0, 1}, B = {1, 2}
e C = {0, 2}, então o conjunto (A  B) – (B  C) possui
quantos pares ordenados?
a) 1
b) 2
c) 3
d) 4
e) 5
02. (UCSal-BA) Seja n(A) o número de elementos de um
conjunto A. Se F = {x  z / 0  x + 1  5} e
G = {x  z / 3 < 2x – 1 < 13}, então n[(F  G)  (G – F)]
é:
a) 1
b) 2
c) 3
d) 4
e) 5
03. (Consultec-BA) Sabendo que A e B são dois conjuntos
tais que:
1o
) (1, 7), (5, 3) são elementos de A  B
2o
) A  B = {1, 3}, podemos afirmar, com toda
segurança, que:
a) A  B tem 8 elementos;
b) A  B tem mais de 8 elementos;
c) A  B tem menos de 8 elementos;
d) A  8 tem 9 elementos;
e) nada se pode afirmar sobre o número de elementos
de A  B.
04. Considerem-se os conjuntos P = {x  N / 1  x, < 6} e
S = (x  z / – 4 < x < 5}. Sendo M = (S – P)  S,
pode-se afirmar que:
a) (1, – 2)  M
b) {(2, 3)}  M
c) {– 2, 1} M
d) (0, 4)  M
e) {(3, – 3)}  M
05. (Consultec-BA) Se A  B = {(1, 2), (1, 4), (2, 2), (2, 4)}
e C = {0, 1}, qual o conjunto B  (C – A)?
a) {(2, 0), (4, 0)}
b) {(1, 0), (2, 0), (3, 0), (4, 0)}
c) {(1, 0), (2, 0)}
d) {(3, 1), (4, 1)}
e) {0, 2, 4}
06. (Consultec-BA) Sendo A = {x  R; – 2 < x < 2) e
B = {x  Z; – 2 < x  6}, então o gráfico de A  B é:
a)
b) d)
c) e)
07. (Consultec-BA) Sendo A= {1, 2} e B = {x  R; x > –2},
o gráfico correspondente ao produto A  B é:
a)
b) d)
c) e)

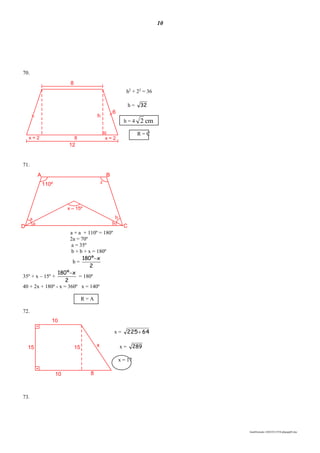
2. 2
08. (Consultec-BA) Sendo M = {x  R; – 2 < x < 2},
N = [0; 3], a melhor representação gráfica M  N é:
a) c)
b) d)
09. São dados os conjuntos A = {2, 3, 4} e B = {5, 6, 7, 8, 9} e
a relação R= {(x, y)  A  B / x e y são primos entre si}.
Um dos elementos dessa relação é o par ordenado:
a) (9, 4)
b) (5, 4)
c) (4, 7)
d) (3, 6)
e) (2, 8)
10. Seja B um subconjunto de A.
Se {(0, 6), (2, 8), (4, 10)}  A  B e n (A  B) = 18,
temos:
a) n(A) = 3
b) n(A) = 6
c) n(A) = 9
d) n(B) = 6
e) n(B) = 9
11. Dado um conjunto C, denotemos por n[P(C)] o número
de elementos do conjunto das partes do conjunto C.
Sejam A e B, com A  B, dois conjuntos não vazios de
tal forma que: n[P(A  B)] = 128.
Calcule:
  
  APn
BPn
12. Os conjuntos A, B, A  B e A  B têm,
respectivamente, (x + 3), (x – 2), (x2
– 9) e 2 elementos.
O número de elementos do conjunto A  B é:
a) primo;
b) menor que 8;
c) maior que 10;
d) múltiplo de 3;
e) quadrado perfeito.
13. (UFC-CE) Sejam N o conjunto dos números inteiros
positivos e E = {(x, y)  N2
; x4
y4
– 10x2
y2
+ 9 = 0}.
Determine o número de elementos de E.
14. (Consultec-BA) Sejam os conjuntos A = {1, 2} e
B = {0, 1, 2}. Qual das alternativas abaixo é verdadeira?
a) f : x  2x é uma função de A em B.
b) f : x  x + 1 é uma função de A em B.
c) f : x  x2
– 3x + 2 é uma função de A em B.
d) f : x  x2
– x é uma função de B em A.
e) f : x  x – 1 é uma função de B em A.
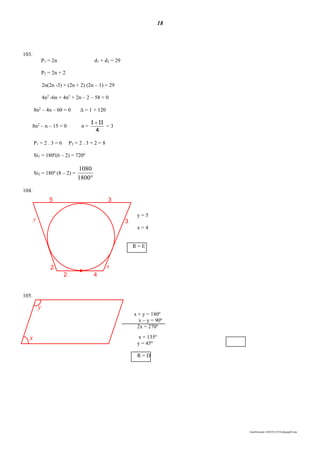
15. (Fuvest-SP) A altura de uma árvore, em metros, é dada
pela fórmula ,
t10
100
10h

 onde t é a idade em anos.
a) Qual a altura da árvore aos 10 anos de idade?
b) Qual a altura máxima que a árvore pode atingir?
16. (Fuvest-SP) As funções f e g são dados por f(x) = 1
5
x3

e g(x) = .a
3
x4

Sabe-se que f(0) – g(0) = .
3
1
Os valores de
f(3) 






5
1
g3 é:
a) 0
b) 1
c) 2
d) 3
e) 4
17. (Vunesp) Considere a função f : R  R, definida por
f(x) = 2x – 1. Determine todos os valores de m  R para
as quais é válida a igualdade: f(m2
) – 2f(m) + f(2m) = .
2
m
18. (FCMSC) Seja a função f, de R em R, definida por:
f(x) =





0xse,1x
0xse,1x2
A soma f 






2
1
+ f(0) + f(1) é igual a:
a) 4
b) 5 d) 6
c) 5,5 e) 7,5
19. (Consultec-BA) Dada a função f, de R em R, definida
por:
f(x) =






'2
1
Qxsex
Qxsex
o número
m = f  3f
2
1






é tal que:
a) m < 0
b) 0 < m < 1 d) 2 < m < 3
c)
2
1
< m < 3 e) m > 3

3. 3
20. (Vunesp) Se f: R  R é uma função definida pela
expressão f(x – 2) = x3
, então o valor de f(3) é igual a:
a) 1
b) 27
c) 8
d) 125
e) 0
21. (Mackenzie-SP) O gráfico abaixo representa uma
função definida em R por y = f(x). O valor de f(2) +
f(f(– 5)) é igual a:
a) – 2
b) – 1
c) 0
d) 1
e) 2
22. (UFSC) Considere a função f(x) real, definida por
f(1) = 43 e f (x + 1) = 2f(x) – 15. Determine o valor de
f(0).
a) 25
b) 27
c) 29
d) 31
e) 33
23. (Fuvest-SP) Uma função f de variável real satisfaz a
condição f(x + 1) = f(x) + f(1), qualquer que seja o
valor da variável x. Sabendo-se que f(2) = 1, podemos
concluir que f(5) é igual a:
a)
2
1
b) 1
c)
2
5
d) 5
e) 10
24. Analise o gráfico e a tabela:
Combustível Preço por litro (em reais)
Gasolina 1,50
Álcool 0,75
De acordo com esses dados, a razão entre o custo do
consumo, por km, dos carros a álcool e a gasolina é
igual a:
a)
7
4
b)
7
5
d)
10
7
c)
8
5
e)
10
9
25. O domínio da função dada por y =
1x
1
1x
x3
22 


é:
a) {x  R / x2
 1}
b) {x  R / x   1}
c) {x  R / x2
= 1}
d) R
e) R – {1}
26. (UFCE-adaptado) O domínio da função real
g(x) =
7x
2x


é:
a) {x  R / x > 7}
b) {x  R / x  2} d) {x  R / 2  x ou x  7}
c) {x  R / 2  x < 7} e) {x  R / x  7}
27. (ESPM-SP) Qual o domínio de validade da função
f(x) =
3
3x
x1


real?
28. O domínio da função dada por f(x) =
x2
1x


é:
a) {x  R / – 1  x  2}
b) {x  R / – 1  x < 2}
c) {x  R / 1  x 1  x < 2}
d) {x  R*/ x  2}
e) {x  R /x  2}

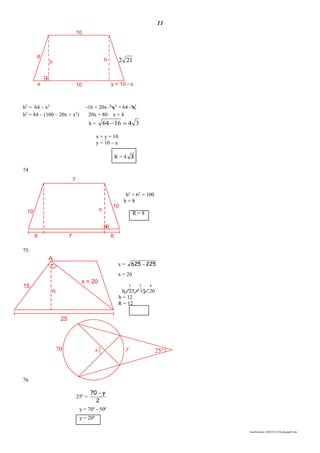
4. 4
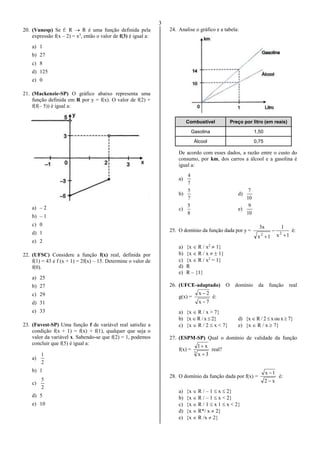
29. (Fuvest-SP) Considere a função f dada por:
f(x) = .
x
5
1x
9x
1x
12
1x





Determine seu domínio de validade.
30. Determinar o domínio da função: f(x) = .
3x2x
5
2

31. (Mackenzie-SP) Se y = ,
1x
x
2


então, o conjunto de
todos os números reais x para os quais y é real é:
a) {x  R / x  0 e x  – 1}
b) {x  R / x  1 e x  – 1}
c) {x  R / x < 0 e x  – 1}
d) {x  R / – 1< x < 1}
e) 
32. O domínio da função real f(x) =
x1
1
x3

 é:
a) R+
b) R+ – {1}
c) {x  R / x  1 e x  0}
d) {x  R / x > ou x < – 1}
e) {x  R / x < 1}
33. O domínio da função dada por y = 4xx  é:
a) D = {x  R / x  0}
b) D = {x  R / x  0}
c) D = R
d) D = {x  R / x > 0}
e) D = {x  R / x  4}
34. Se f(x) = 35
23
xx
xx2


é uma função de x em R, então x é
o conjunto:
a) {x  R / x  0}
b) {x  R / x  0 e x   1}
c) {x  R / 0 < x < 1 e x > – 1}
d) {x  R / x > l ou x < – 1}
e) {x  R / – 1 < x < 0 ou x > 1}
35. (PUC-SP) Qual o domínio da função real
f: x    ?1x
23

36. (Consultec-BA) O conjunto imagem da função
2
1x3
y

 é:
a) R
b) R – {2}
c) R+
d) R–
e) R – {3}
37. (Consultec-BA) O conjunto imagem da função
3x
1x2
y


 é:
a) R – {3}
b) R – {– 3}
c) R – {2}
d) R – {– 2}
e) R
38. (FBDC-BA) Dada a função f(x) = ,
2x
2x3


o valor do
domínio da função que tem imagem igual a
3
1
é:
a)
2
1
b)
2
1
 d) – 1
c)
3
1
e) 1
39. (UCSal-BA) A imagem da função f(x) = x2
– 4 é:
a) [– 4, + [
b) ]– ; – 4]
c) [4, + [
d) ]– ; 4]
e) ]4; + [
40. (Consultec-BA) A soma sen 75° – cos 75° é igual a:
a)
2
2
b)
2
3
c)
2
6
d)
2
1
e) 0
41. (UCSal-BA) Calculando-se (sen 15° + cos 15°)2
,
obtém-se:
a)
2
1

b) 1
c)
2
1
d)
2
3
e) 0
42. (Consultec-BA) Se x = cos ;
2

y = sen ;
2

e a = sen ,
o valor da expressão (x – y)2
é:
a) a2
b) a2
– 1
c) t – a2
d) a – 1
e) 1 – a

5. 5
43. (Consultec-BA) Se sen  – cos  = x, então sen 2 é:
a) 2x
b) x2
+ 1
c) 1 – x2
d) x + 1
e) x2
– 1
44. (UCSal-BA) Se tg x = m, então tg 2x é igual a:
a) 2
m1
m2

b) 2
3
m31
mm3


c) 2
3
m31
mm3


d) 2
m1
m2

e) 3 m
45. (UFES) Sabendo que sen  =
13
5
e   2o
quadrante,
o valor da tg
2

é:
a) – 5
b) – 2
c) – 1
d) 2
e) 5
46. (Mackenzie-SP) Se tg x = m e tg 2x = 3 m, m > 0, o
valor do ângulo x é:
a) 30°
b) 45°
c) 60°
d) 90°
e) 15°
47. (FBDC-BA) No triângulo retângulo, sabe-se que
sen  = .
3
1
Determine sen( + 2).
a)
5
1

b)
5
1
c)
3
1
d)
3
1

e) 1
48. (UCSal-BA) Sendo x  [0, ], o número de soluções da
equação sen 2x = cos x é:
a) 0
b) 1
c) 2
d) 3
e) 4
49. O conjunto solução, em R, da equação: 2 sen 03x 
é:
a)








 Zk,k2
3
x/Rx
b)










 Zk,k2
3
5
xouk2
3
4
x/Rx
c)










 Zk,k2
3
5
xouk2
3
4
x/Rx
d)










 Zk,k2
3
2
xouk2
3
x/Rx
e)








 Zk,k
3
k4
x/Rx
50. O conjunto solução, em R, da equação 2 cos(3x) – 1 = 0
é:
a)










 Zk,
3
k2
12
x/Rx
b)








 Zk,
12
k
x/Rx
c)










 Zk,
2
k
6
x/Rx
d)








 Zk,k
12
x/Rx
e)








 Zk,k2
12
x/Rx
51. O conjunto solução, em R, da equação
tg 01
4
x2 




 
 é
a)








 Zk,k
4
x/Rx
b)










 Zk,
2
k
8
x/Rx
c)










 Zk,
2
k
8
x/Rx
d)








 Zk,
2
k
x/Rx
e)








 Zk,k2
4
x/Rx

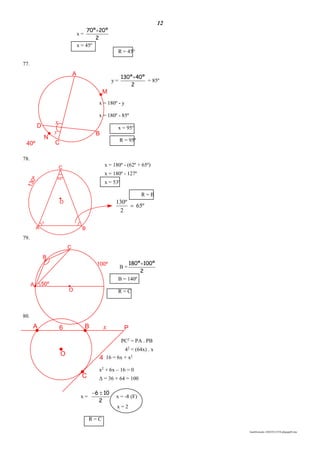
6. 6
52. (Fatec-SP) Se x é um número real tal que sen2
x – 3
sen x = – 2, então x é igual a:
a)
2

+ h, h  Z
b)
2
3
+ h, h  Z
c)
2
3
+ h  2, k  Z
d)
2

+ h  2, k  Z
e)
4

+ h, k  Z
53. (Consultec-BA) As soluções da equação tg x + cotg x = 2,
compreendida no intervalo ,
2
,
2 




 
 são:
a)
4


b)
4

c)
2

d)
2


e)
3

54. (Consultec-BA) O conjunto solução da equação
sen x  tg x + 2  cos x = 2, no intervalo fechado [0, 2],
é:
a) {0, 2}
b) {0, – , 2}
c) {}
d)






2
e)





 
4
5
55. (Consultec-BA) O número de soluções da equação
cos 4x = 0, no intervalo [0, ], é:
a) 3
b) 4
c) 5
d) 6
e) 7
56. (UCSal-Ba) As soluções da equação
2  sen x  cos x – sen x = 0, no intervalo [0; 2], são:
a)










2,
3
5
,,
3
,0
b)





 


3
5
,,
3
,0 d)





 

6
,,0
c)








 2,
6
11
,
6
,,0 e) 
57. (UCSal-BA) O valor da expressão
    




 





 
4
sec2tgcos
2
sen é:
a) – 1
b) 9 d) 21
c) 17 e) 22
58. (Consultec-BA) A tangente de
4
9
é igual a:
a) – 1
b)
2
1
 d)
2
1
c) 1 e)
2
2
59. (UCSal-BA) O valor de tg 3.520° é igual ao valor de:
a) – tg 8°
b) – tg 80° d) tg 10°
c) – tg 10° e) tg 80°
60. (FBDC-BA) O sen de 813° é igual ao:
a) co-seno de 5°.
b) co-seno de 7°. d) seno de 93°.
c) co-seno de 87°. e) seno de 98°.
61. (UCSal-BA) Se A = sec 420°, então A é igual a:
a) 2
b)
3
32
d)
2
3
c) 1 e)
2
1
62. (Consultec-BA) sen 135° – cos 225° é igual a:
a)
2
2
b)
2
2
 d) 2
c) 0 e) 2
63. (Consultec-BA) O valor de sen 330° – cos 2.460° é:
a) 0
b) – 1 d)
2
3
c) 1 e)
2
3

64. (Consultec-BA) A simplificação da expressão
A= sen (900° – x) + cos (1.980° + x) + sen (1.440° – x) é:
a) cos x.
b) sen x. d) sen x.
c) –tgx. e) – cos x.

7. 7
65. Simplifique a expressão:
     
   









2secgcot
2
sen
2tgseccos
E
66. (Fatec-SP) Calcule o valor da expressão:
3
2
gcot
2
eccos2sec
3
2
tg
4
5
cos
2
3
sen
E










67. (UCSal-BA) A área do paralelogramo ABCD, na figura
abaixo, é 30 cm2
.
A área do trapézio retângulo EBCD é:
a) 34 cm2
b) 38 cm2
c) 54 cm2
d) 60 cm2
e) 70 cm2
68. (Consultec-BA) Se ABCD é trapézio de bases AB e
,CD determine x + y.
a) 195°
b) 185°
c) 175°
d) 165°
e) 155°
69. (Consultec-BA) Em um trapézio retângulo, a bissetriz de
um ângulo reto forma, com a bissetriz do ângulo agudo
do trapézio, um ângulo de 110°. O menor ângulo desse
trapézio é:
a) 130°
b) 110°
c) 80°
d) 60°
e) 50°
70. (Consultec-BA) A base maior de um trapézio isósceles
mede 12 cm e a base menor 8 cm. O comprimento de
cada lado não paralelo é 6 cm. O valor da altura é:
a) 22 cm
b) 23 cm
c) 24 cm
d) 25 cm
e) 26 cm
71. (FBDC-BA) ABCD é trapézio de bases AB e .CD Se
DP e CP são bissetrizes, o valor de x é:
a) 140°
b) 130°
c) 120°
d) 110°
e) 100°
72. Um trapézio retângulo de 15 cm de altura tem as bases
medindo 10 cm e 18 cm. Determine a medida do lado
oblíquo às bases.
73. Determine a altura do trapézio da figura.
74. As bases de um trapézio isósceles medem 7 e 19 e os
lados não paralelos, 10. Calcule a altura desse trapézio.

8. 8
75. No trapézio ABCD abaixo, a diagonal AC é
perpendicular ao lado oblíquo .AD Sendo CD = 25 cm e
AD = 15 cm, determine a medida da altura do trapézio.
76. Na figura abaixo, calcule o valor de x.
77. (UFBA) Na figura abaixo, o arco AMB mede 130° e o
arco CND mede 40°. Calcule o número que expressa a
medida do ângulo x.
78. (UEFS-BA) Na figura abaixo, em que se tem um círculo
de centro O, o arco AC mede 130° e o ângulo BCˆA
mede 62°. A medida x do ângulo BÂC é:
a) 65°
b) 53°
c) 50°
d) 31°
e) 28°
79. (UEFS-BA)
Na figura, O é o centro da circunferência.
Portanto, o ângulo ABC mede:
a) 120°
b) 130° d) 150°
c) 140° e) 160°
80. (UCSal-BA) Na figura a seguir, são dados: PC = 4 cm
e AB = 6 cm.
A medida do segmento PB, em cm, é:
a) 1
b) 1,5
c) 2
d) 2,5
e) 3
81. (FBDC-BA) Os ângulos internos de um triângulo ABC
medem: Â = 30°, Bˆ = 70° e Cˆ = 80°. Uma
semicircunferência de diâmetro AB intercepta os
outros dois lados em P e Q.
A medida do arco PQ é igual a:
a) 35°
b) 25°
c) 20°
d) 15°
e) 10°
82. (FBDC-BA) Sendo O1 e O2 os centros das
circunferências da figura, calcule x.

9. 9
83. Calcule o número de diagonais (d) e a soma das medidas
dos ângulos internos (Si) de cada um dos polígonos
convexos.
a) Eneágono
b) Dodecágono
84. Qual é a soma das medidas dos ângulos internos do
polígono que tem o número de diagonais igual ao
quádruplo do número de lados?
85. Qual é o polígono convexo que possui 170 diagonais?
86. Calcule o número de diagonais de um polígono convexo,
sabendo-se que a soma das medidas dos ângulos internos
é 1.800°.
87. Calcule o valor de x na figura a seguir:
88. O ângulo interno de um polígono regular vale 1,5 vez o seu
ângulo externo. Determine o número de lados do polígono.
89. O ângulo externo de um polígono regular é igual ao
dobro do seu ângulo interno.
Determine o número de diagonais desse polígono.
90. Determine a medida do ângulo formado pelas diagonais
AC e BF de um octógono regular ABCDE...
91. (Uneb-BA) Dizemos que um polígono pavimenta ou
ladrilha um plano se cópias congruentes desse polígono,
adaptadas lado a lado, cobrem o plano sem deixar
buracos e sem a necessidade de superposições. Assinale
a alternativa que contém um polígono que pavimenta ou
ladrilha um plano.
a) Pentágono
b) Eneágono
c) Pentadecágono
d) Hexágono
e) Octógono
92. (UFMG-Adaptada) Observe a figura a seguir.
O triângulo ABC está inscrito num semicírculo de
diâmetro AB e centro O. A medida do ângulo CÔA é
120º. O ângulo BÂC mede:
a) 90º
b) 60º
c) 30º
d) 45º
e) 15º
93. (UNEB) Em um circulo de centro O, figura abaixo, está
inscrito o ângulo .
Se o ângulo AÔB mede 80º, então  mede:
a) 30º
b) 40º
c) 45°
d) 50°
e) 60º
94. Na figura abaixo, o valor de x – y é:

10. 10
A
B
C D
P

5
x
3
4
y
A
P
Q
B
4 M x
3
5 O
8
y
2
3
x
6

95. O valor de  na figura, onde "O" é o centro da
circunferência é:
a) 15°
b) 21°
c) 30°
d) 42°
e) 84°
96.
Na figura, a reta r é tangente à circunferência no ponto T
e faz com a corda TM um ângulo  = 68°. Nessas
condições, o ângulo  mede, em graus:
a) 102
b) 112
c) 124
d) 136
e) 148
97. Qual é o polígono regular cuja medida do ângulo interno
é o triplo da medida do ângulo externo?
98. Determine o polígono cujo número de diagonais é igual
ao dobro do número de lados.
99. Dois polígonos têm a quantidade de lados representados
por dois números inteiros e consecutivos. Sabendo que
a soma dos ângulos internos desses dois polígonos
juntos é igual a 1620°, determine o número de diagonais
do polígono com maior número de lados.
100.Sabendo que AB e CD são, respectivamente, os lados
de um pentágono regular e de um eneágono regular, a
medida do ângulo ,DPˆB em graus, é igual a:
a) 56º
b) 72º
c) 40º
d) 116º
e) 124º
101.Os valores de x e y na figura abaixo são, respectivamente
iguais a:
a) 7 e 10
b) 9 e 6
c) 5 e 7
d) 6 e 10
e) 7 e 9
102.Sendo O o centro da circunferência abaixo, o valor de x é:
a) 2
b) 4
c) 8
d) 6
e) 10
103.Dois polígonos possuem a quantidade de lados
representados por números pares e consecutivos. Sabendo
que os polígonos têm juntos 29 diagonais, a soma dos
ângulos internos desses dois polígonos é igual a:
a) 900º
b) 1080º
c) 360º
d) 1800º
e) 720º
104.Na figura abaixo, os valores de x e y são, respectivamente:
a) 7 e 2
b) 5 e 4
c) 3 e 6
d) 6 e 3
e) 4 e 5
105.Num paralelogramo, a diferença entre as medidas de dois
ângulos consecutivos é igual a um ângulo reto. As medidas
desses ângulos são:
a) 120º e 30º
b) 145º e 55º
c) 115º e 25º
d) 135º e 45º
e) 130º e 40º

11. 11
GABARITO
0 1 2 3 4 5 6 7 8 9
0 – C D B D A B C C C
1 B 64 C 3 C  E  B E
2 D C C C D D A  C 
3 R A E E B  A C E A
4 A D E C A E A C D C
5 A D D B A B A A C B
6 D A E B E  2
23
C B E
7 C A 17 34
8 12 45o
95o
B C
8 C C 19o
 1620o
 54 90o
5 0
9 90o
D C D 45o
B D   14
10 E B C D E D – – – –
15. a) 5 m
b) 10 m
17. m = 0 ou m =
4
1
27. D = [– 1; + [
29. D = R – {– 5, – 1, 0, 1}
35. D = {1}
65. E = – tg2
x
83. a) 27 diagonais e 1260o
b) 54 diagonais e 1800º
85. icoságono
97. octógono regular
98. heptágono

12. Resolução Comentada
01. A x B = {(0,1), (0,2), (1,1), (1,2)}
B x C = {(1,0), (1,2), (2,0), (2,2)}
(A x B) – (B x C) = {(0,1), (0,2), (1,1)}
R = C
02. F = {X E Z / – 1  x  4} = {– 1, 0, 1, 2, 3, 4}
G = {X E Z / 2 < x < 7} = {3, 4, 5, 6}
F  G = {3,4}
G – F = {5,6}
n [(F  G) x (G – F)} = 2 . 2 = 4
R = D
03. A = {1, 5, 3, ...}
B = {7, 3, 1, ...}
R = B
04. P = {1, 2, 3, 4, 5}
S = {– 3, – 2, – 1, 0, 1, 2, 3, 4}
M = {– 3, – 2, – 1, 0} x {– 3, – 2, – 1, 1, 2, 3, 4}
(0,4) M
R = D
05. A = {1,2}, B = {2,4} e C = {0,1}
C – A = {0}
B x (C – A) = {(2,0), (4,0)}
R = A
06. A = ]– 2, 2 [ B = {– 1, 0, 1, 2, 3, 4, 5, 6}
-2
2
A
B
R = B
07. A = {1, 2} e B = ]– 2, +  [
B
A
-2
0 1 2
R = C
08. M = [– 2, 2] N = [0, 3]
N
-2
2 M
R = C
09. R = {(2,5), (2,7), (2,9), (3,5), (3,7), (3,8), (4,5), (4,7),
(4,9)}
R = C
10. A = {0, 2, 4, ...}
B = {6, 8, 10, ...}
BA  n(B)  n(A)
n(B) = 3 e n(A) = 6
n(A) . n(B) = 18
R = B
11. A  B  n(A)  n(B)
n[P(A)]  corresponde ao no
de subconjuntos 
2n(A)
n[P(A x B)] = 2n(A).n(B)
= 27
 n(A) . n(B) = 7 
n(A) = L e n (B) = 7
64
2
128
2
2
2
2
1
7
 )(
)(
)]([
)]([
An
Bn
APn
BPn
R = 64
12. n(A) = x + 3 n(B) = x – 2 n(A  B) = x2
– 9
n(A  B) = 2
n(A  B) = n(A) + n(B) – n(A  B)
x2
– 9 = x + 3 + x – 2 – 2
x2
– 2x – 8 = 0
 = 4 + 32 = 36
R = C
13. E = {(x,y)  N* x N* / (xy)4
– 10 (xy)2
+ 9 = 0
(x . y)2
= a  a2
– 10a + 9 = 0
(x . y)2
= 1 ou (x,y)2
= 9
x . y = 1 ou x . y = – 1 ou x . y = 3 ou x . y =
– 3
(1,1)
R = {(1,1), (1,3), (3,1)}
R = 03
x = 4(V)
x = – 2(F)
n(A) = 4 + 3 = 7
n(B) = 4 – 2 = 2
n(A x B) = 7 . 2 = 14
a = 1
a = 9
(F) (1,3), (3,1) (F)

13. 2
lmat03estudo-140325213554-phpapp02.doc
14.
1 ·
2 ·
· 0
· 1
· 2
a)
A B
1 ·
2 ·
· 0
· 1
· 2
b)
A B
1 ·
2 ·
· 0
· 1
· 2
c)
A B
X
· 1
· 2
d)
AB
0 ·
1 ·
2 ·
· 1
· 2
e)
AB
0 ·
1 ·
2 ·
R = C
15.
a) h(10) = 10 –
1010
100

= 10 – 5 = 5 m
b) h(0) = 10 –
10
100
= 0
h(20) = 10 –
30
100
= 10 –
3
10
=
3
20
m
h(40) = 10 –
50
100
= 10 – 2 = 8 m
h(90) = 10 –
100
100
= 10 – 1 = 9 m
h(990) = 10 –
1000
100
= 10 – 0,1 = 9,9 m →
aproximadamente 10m
16. f(0) =
5
0.3
– 1 = – 1 g(0) =
3
0.4
+ a = a
– 1 – a =
3
1
 a =
3
1
– 1 a =
3
4
f(3) =
5
3.3
– 1 =
5
4
g 





5
1
=
5
4
f(3) – 3 . g 





5
1
=
5
4
– 3 . 




 
155
16
=
5
20
= 4
R = E
17. f(x) = 2x – 1  f(m2
) – 2 f(m) + f(2m) =
2
m
2m2
– 1 – 4m + 2 + 4m – 1 =
2
m
2m2
=
2
m
4m2
– m = 0
18. f 




 
2
1
= – 2 . 




 
2
1
+ 1 = 2
f(0) = – 2 . 0 + 1 = 1
f(1) = 1 + 1 = 2
2 + 1 + 2 = 5
R = B
19. f 





2
1
=
1
2
1







= 2
f     333
2

m = 2 + 3 = 5
R = E
20. x = 5  f(5 – 2) = 53
= 125
R = D
21. f(2) + f(f(–5)) = – 3 + 3 = 0
f(2) = – 3
f(– 5) = 5
f(f(– 5)) = f(5) = 3
R = C
22. f(x + 1) = 2 . f(x) – 15
x = 0  f(1) = 2 . f(0) – 15
43 = 2 . f(0) – 15
f(0) =
2
1543 
f(0) = 29
R = C
23. f(x+1) = f(x) + f(1)
x = 1 f(2) = f(1) + f(1)  f(1) =
2
1
x = 2  f(3) = f(2) + f(1) = 1 +
2
1
=
2
3
x = 3  f(4) = f(3) + f(1) =
2
3
+
2
1
= 2
x = 4  f(5) = f(4) + f(1) = 2 +
2
1
=
2
5
R = C
24. C(G) =
1400
150
14
50,1

C(A) =
40
3
1000
75
10
75,0

)G(C
)A(C
=
10
7
15
140
.
40
3
140
15
40
3

25. y =
1x
x3
2

–
1x
1
2

D = R
26. g(x) =
7x
2x


1- x – 2  0  x  2
2- x – 7 > 0  x > 7
m = 0
m =
4
1
2 5

14. 3
lmat03estudo-140325213554-phpapp02.doc
D = {X  R/ x > 7}
R = A
27. f(x) =
3
3x
x1


1- 1 + x  0  x  – 1
2- x + 3  0  x  – 3
D = [– 1, +  [
28. f(x) =
x2
1x


1- x – 1  0  x  1
2- 2 – x > 0 2 > x  x < 2
D = {X  R/ 1  x < 2}
R = C
29. x + 1  0  x  – 1
x  0



x
5
1x
9x
0  x2
+ 9x – 5x – 5  0
x2
– 4x – 5  0
x  – 5 ou x  1
D = R – {– 5, 1, 0, – 1}
30. f(x) =
03x2x
5
2

R
 = 4 – 12 = – 8
D = R
31. y =
1x
x
2


1- – x  0  x  0
2- x2
– 1  0  x   1
D = {X  R / – 1  x  0}
R = A
32. f(x) =
x1
1
x3


1 – x > 0  1 > x  x < 1
D = {X  R / x < 1}
R = E
33. y = x + 4x 
1- x  0
2- x – 4  0  x  4
D = {X  R / x  4}
R = E
34. y =
0xx
xx2
35
23


x3
(x2
– 1)  0
x  0 e x   1
D = {X  R / x  0 e x   1}
R = B
35. y = 0)1x( 23

(x3
– 1)2
 0
x3
– 1 = 0
x = 1
D = {1}
36. y =
2
1x3 
3x – 1 = 2y
x =
3
1y2 
Im = R
R = A
37.
3x
1x2
1
y



xy + 3y = 2x – 1
xy – 2x = – 3y – 1
02y
1y3
x



y  2
Im = R – {2}
R = C
38.
3
1
2x
2x3



9x – 6 = x + 2
8x = 8
x = 1
R = E
39. y = x2
– 4
x2
= y + 4
x = 04y 
y  – 4
Im = [– 4, +  [
R = A

15. 4
lmat03estudo-140325213554-phpapp02.doc
40. sen 75º = sen(45º + 50º) = sen 45º cos 30º + sen 30º
cos 45º
=
4
26
2
1
.
2
2
2
3
.
2
2 

cos 75º = cos(45º + 30º) = cos 45º cos 30º – sen 45º
sen 30º
=
4
26
2
1
.
2
2
2
3
.
2
2 

sen 75º  cos 75º =
2
2
4
2626


R = A
41. (sen 15º + cos 15º)2
= sen2
15º + cos2
15º + 2sen 15º
cos 15º
= 1 + sen 30º = 1 +
2
1
=
2
3
R = D
42. 




 


2
2
sen
2
cos cos2
2

+ sen2
2

– 2sen
2

cos
2

= 1 – sen 
= 1 – a
R = E
43. (sen  – cos  )2
= x2
sen2
 + cos2
 – 2sen  cos  = x2
1 – sen 2  = x2
sen 2  = 1 – x2
R = C
44. tgx = m
tg2x = 22
m1
m2
xtg1
tgx2



45. sen  =
13
5
cos  = –
169
25
1
cos  =
13
12
tg
2

= + 5
1
25
13
12
1
13
12
1







 

R = E
46. tg2x =
x2tg1
tgx2

 2
m41
m2
1
m3


2 = 3 – 3m2
3m2
= 1
m =
3
3

tgx =
3
3
 x = 30º
R = A
47. sen  =
3
1
 cos  =
3
22
cos =
3
1
sen =
3
22
sen(  + 2 ) = sen  cos2 + sen2  cos 
sen(  + 2 ) =
3
1
27
9
27
167
3
22
.
9
24
9
7
.
3
1 









 
*cos2 = cos2
 – sen2
 =
7
1
9
8
9
1 

*sen2 = 2.sen cos = 2 .
9
24
3
22
.
3
1

R = C
48. sen 2x = cos x  2 sen x cos x – cos x = 0
cos x(2 sen x – 1) = 0
30º
90º
150º
R = {30º, 90º, 150º}
R = D
49. 2 sen x = – 3
sen x =
2
3
{X  R / x =
3
4
+ 2K  ou x =
3
5
+ 2K  . K  Z}
R = C
50. cos(3x) =
2
1
 cos a =
2
2
a = 
4

+ 2K   3x = 
4

+ 2K 
m =
3
3
(V)
m =
3
3
(F)
cos x = 0
cos x =
2
1
3
π
3
π5
3
π
π2 
3
π4
3
ππ



16. 5
lmat03estudo-140325213554-phpapp02.doc
x = 
12

+
3
K2 
R = A

17. 4
π
π 0
3
π
π2
3
5
3
2




51. tg(2x +
4

) = 1 tg a = 1
a =
4

+ k   2x +
4

=
4

+ k 
x =
2
k
, k ε Z R = D
52. sen2
x – 3 sen x + 2 = 0
sen x =
2
13
sen x = 2 (F)
sen x = 1 x =
2

+ 2k 
R = D
53. tg x + cotg x = 2  tg x 
tgx
1
= 2
tg2
x – 2 tg x + 1 = 0 Δ = 0
tg x = 1
R:
4

R = B
54. sen x . tg x + 2cos x = 2
sen x .
x
xsen
cos
+ cos2
x – 2 = 0
sen2
+ 2cosx – 2 = 0 1 – cos2
x + 2 cos x – 2 = 0
cos2
x – 2cos x + 1 = 0 Δ = 0
cos x =1 x = 0 + 2k  S = {0,2  }
R = A
55. cos 4x = 0 → cos a = 0
a =
2

k  4x =
2

+ k 
x =
8

+
4
k

18. 7
lmat03estudo-140325213554-phpapp02.doc
k = 0 → x1 =
8

k = 1 →x2 =
8

+
4

k = 2 → x3 =
8

+
2

k = 3 → x4 =
8

+
4
3
R = B
56. 2sen x cos x – sen x = 0 sen x = 0
sen x (2cos x – 1) = 0 cos x =
2
1
S = {
3
,0

,
3
5
, , 2 }
R = A
57. 





2

sen . (cos π) + (tg2 π) . sen 





4

= 1. (-1) + 0 . 2 = -1
R = A
58.
4
π9
=
4
π8
+
4
π
tg
4
π9
= tg
4
π
= 1
R = C
59. 3520º 360º
280º 9

19. 8
lmat03estudo-140325213554-phpapp02.doc
tg3520º = tg 280º = -tg 80º
R = B
60. 813º 360º
7200
2
930
sen 813º = sen 93º = sen (180º – 93º ) = sen 87º = cos3º
R = D
61. 420º 360º
60º 1º
sec 460º = sec 60º =
60cos
1
=
2/1
1
= 2
R. = A
62. sen 135º= 45º =
2
2
cos 225º = – cos 45º =
2
2
2
2
–







 
2
2
=
2
22
= 2
R = E
63. sen 330º = – sen 30º =
2
1

2460º 360º
2160º 6
300º
cos 2460º = cos 300º = + cos 60º = +
2
1
2
1
– 






2
1
= 0
R = C
64. sen (900º – x) = sen (180º – x) = sen x
cos (1980º – x) = cos (180º – x) = – cos x
sen (1440º – x) = sen (360° – x) = – sen x
A = sen x – cos x – sen x
A = – cos x
R =E

20. 9
lmat03estudo-140325213554-phpapp02.doc
10
8 B
C
D
A
6
30 cm2
110º
25º
45º
65. E =











 





 







xsenx
x
x
x
senx
x
x
cos
1cos
)(cos
coscos
1
)cos(
E = –
xcos
senx
.
x
senx
cos
= – tg2
x
66. E =


















3
3
).1).(1(
)3.(
2
2
).1(
= –
2
3.2
.
3
3
=
2
23
67.
AΔ =
2
8.6
= 24 cm2
At = 30 + 24 = 54 cm2
R = C
68. x + x + 20º = 180º →2x = 160º
x = 80°
y + y – 30º = 180º →
2y = 210°
y = 105º
x + y = 105º + 80º
x + y = 185º
R = B
69.
R: 25º + 25º = 50º
R = E

21. 10
lmat03estudo-140325213554-phpapp02.doc
8
6
h
12
x = 2 8 x = 2
A B
D C
110º x
x – 15º
b
b
a
a
10
x
810
15 15
70.
h2
+ 22
= 36
h = 32
h = 4 cm2
R = C
71.
a + a + 110º = 180º
2a = 70º
a = 35º
b + b + x = 180º
b =
2
xº180 
35º + x – 15º +
2
xº180 
= 180º
40 + 2x + 180º - x = 360º x = 140º
R = A
72.
x = 64225
x = 289
x = 17
73.

22. 11
lmat03estudo-140325213554-phpapp02.doc
7
10
h10
6 7 6
A
15
h
x = 20
25
10
8
h
10
h
x y = 10 - x
212
h2
= 64 – x2
-16 + 20x – x2
= 64 –x2
h2
= 84 – (100 – 20x + x2
) 20x = 80 x = 4
h = 341664 
x + y = 10
y = 10 – x
R = 4 3
74
h2
+ 62
= 100
h = 8
R = 8
75.
x = 225625 
x = 20
5 3 4
h . 25 = 15 . 20
h = 12
R = 12
76.
x70 25ºy
25º =
2
y70 
y = 70º - 50º
y = 20º

23. 12
lmat03estudo-140325213554-phpapp02.doc
A
B
C
D
M
x
y
N
40º
50º
100º
B
O
A
C
O
C
4
PxB6A
BA
O
62º
x
C
130º
º65
2
º130

x =
2
º20º70 
x = 45º
R = 45°
77.
y =
2
º40º130 
= 85º
x = 180º - y
x = 180º - 85º
x = 95º
R = 95º
78.
x = 180º - (62º + 65º)
x = 180º - 127º
x = 53º
R = B
79.
B =
2
º100º180 
B = 140º
R = C
80.
PC2
= PA . PB
42
= (64x) . x
16 = 6x + x2
x2
+ 6x – 16 = 0
Δ = 36 + 64 = 100
x =
2
106 
x = -8 (F)
x = 2
R = C

24. 13
lmat03estudo-140325213554-phpapp02.doc
80º
70º30º
O
180º
x Q
BA
C
P
81.
80º =
2
xº180 
x = 180º-160º
x = 20º
R = C
82.
38º19º 78º
76º
38º
O
2
x = 19º
83. d =
 
2
3nn
Si = 180º(n-2)
a) n = 9 →d =
2
)39(9 
= 27 Si = 180º(9-2) = 1260º
b) n = 12 → d =
2
)312(12 
= 54 Si = 180º (12 -2) = 1800º
84. d = 4n Si = 180º(11-2)
4n =
2
)3n(n 
Si = 180º . 9
8n = n (n-3) Si = 1620º
n = 11
85. 170º =
2
)3n(n 
n =
2
373 
7
6

25. 14
lmat03estudo-140325213554-phpapp02.doc
A
B H
n2
– 3n – 340 = 0 n = 20
Δ = 9 + 1360
Δ = 1369
R = Icoságono
86. Si = 180º (n -2) d =
2
)312(126

1800 = 180º(n-2) d = 54 diagonais
10
n = 12
87. n = 6 → Si = 180(6 – 2) = 720º
x + x + 40º + 140º + 150º + x + 10º + 110º = 720º
3x + 450º = 720º
3x = 270º
x = 90º
88. a1 =
2
3
ai ai + ae = 180º
Polígono regular
2
3
ae + ae = 180º
ai =
n
Si
=
n
)2n(º180 
3ae + 2ae = 360º
ae =
5
º360
108n = 180n – 360º ae = 720
7n = 360º n = 5 ai = 108º
89. ai = 2ai ai + ai = 180º
ai + 2ai = 180º
ai = 60º
ai =
n
n )2(º180 
ai = 120º
60n = 180n – 360
120n = 360
n = 3 não tem diagonais
90.

26. 15
lmat03estudo-140325213554-phpapp02.doc
x
120º
B
O
C
60º
A
120º
100º
C
B
A
80º
O
80º
120º
D
y
8
º360
= 45º
x =
2
º45º135 
x = 90º
91.polígono regular ai =
n
)2n(º180 
ia
º360
 Z n = 5 →ai =
5
3º.180
= 108º
n = 6 → ai =
6
4.180
= 120º
º120
º360
= 3 Z R = D
92.
x =
2
º60
= 30º
R = C
93.
α = 50º
R = D
94.
y = 30

27. 16
lmat03estudo-140325213554-phpapp02.doc
42º
O
y2
C
o
x x
= 68º
x = 90º - 15º
x = 75º
x – y = 45º
95.
α =
2
º42
 21
R = B
96.
x + 68º = 90º
x = 22º
θ + 2x = 180º
θ = 180º - 44º
θ = 136º
R = D
97. ai = 3ae ai + ae = 180º
3ae + ae = 180º
ae = 45°
ai = 135°
135º =
n
)2n(º180 
135n = 180n – 360
n =
45
º360
= 8 Octógono regular.
98. d = 2n 2n =
2
)3n(n 
n = 7
Heptágono
99. P1 = n Si1 + Si2 = 1620º

28. 17
lmat03estudo-140325213554-phpapp02.doc
40º
C D
x
72º
A B
x
3
7
5
4
o
P2 = n + 1 180º(n – 2) + 180º(n – 1) = 1620º
P1 = 6 180n – 360º + 180n – 180 = 1620º
P2 = 6 + 1 = 7 360ºn = 1620 + 540º
d2 =
2
)37(7 
=
2
28
360ºn = 2160
n = 6 R = 14 diagonais
100.
α =
2
º40º72 
= 56º
x = 180º - 56°
x = 124º
R = E
101.
3
4
y
x
y2
= 4 . 9
y = 6
y2
= 3 (3 + x)
36 = 9 + 3x
27 = 3x
x = 9
102.
5x = 4 . 102
x = 8
R = C

29. 18
lmat03estudo-140325213554-phpapp02.doc
5 3
3
x
y
2
2 4
y
x
103.
P1 = 2n d1 + d2 = 29
P2 = 2n + 2
2n(2n -3) + (2n + 2) (2n – 1) = 29
4n2
-6n + 4n2
+ 2n – 2 – 58 = 0
8n2
– 4n – 60 = 0 Δ = 1 + 120
8n2
– n – 15 = 0 n =
4
111 
= 3
P1 = 2 . 3 = 6 P2 = 2 . 3 + 2 = 8
Si1 = 180º(6 – 2) = 720º
Si2 = 180º (8 – 2) =
1800
1080
104.
y = 5
x = 4
R = E
105.
x + y = 180º
x – y = 90º
2x = 270º
x = 135º
y = 45º
R = D