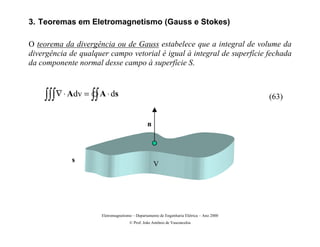
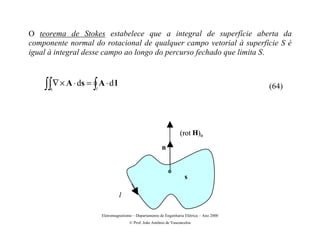
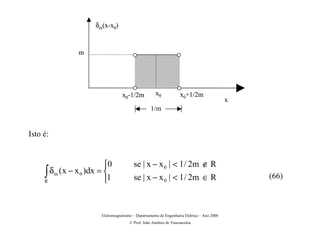
O documento apresenta os principais conceitos matemáticos relacionados ao eletromagnetismo, como operador nabla, gradiente, divergência e rotacional. Explica o significado geométrico e físico dessas grandezas vetoriais diferenciais e mostra exemplos de suas aplicações.



![f = constante, donde podemos concluir que a direção do gradiente dá a máxima
variação df da função f.
∇f // direção de df max . (8)
b) E o módulo do gradiente? O que ele fornece como informação?
Considere o elemento de arco em coordenadas cartesianas
dl=|dl|=[dx2+dy2+dz2]1/2. (9)
Dividindo membro a membro a Eq. (5) pela (9), obtém-se:
∇f ⋅ dl df
= ∇f ⋅ u = . (10)
| dl| dl
Se dl é paralelo ao gradiente de f, logo u é um vetor unitário na direção do
gradiente e o resultado ∇f ⋅ u = ∇f . Portanto, o módulo do gradiente de f dá como
resultado a máxima taxa de variação da função, isto é:
df
∇f = (11)
dl max
Eletromagnetismo – Departamento de Engenharia Elétrica – Ano 2000
© Prof. João Antônio de Vasconcelos](https://image.slidesharecdn.com/eletro1-090731103718-phpapp02/85/Eletromagnetismo-4-320.jpg)


















![Isto se deve ao fato de que os unitários curvilíneos são função do ponto e não
podem portanto serem extraídos da operação de diferenciação. As expressões em
coordenadas curvilíneas podem ser encontradas na página 17 do livro
Eletromagnetismo (Annita Macedo).
O operador ∇ × ∇ , dado em (48), aplicado a uma função de ponto será sempre nulo
se a função for contínua e tiver contínuas as derivadas segundas mistas. Isto só
não ocorre com as grandezas do eletromagnetismo [AnnitaMacedo]. A Tabela a
seguir mostra outras operações possíveis com este operador.
Operações com o Operador Nabla
( ∇ × ∇ )f = ∇ × ( ∇ f ) = 0 (55)
(∇ × ∇) ⋅ A = 0 (56)
(∇ × ∇) × A = 0 (57)
∂Ax ∂Ay ∂A
∇ (∇ ⋅ A) = ∇( ) + ∇( ) + ∇( z ) (58)
∂x ∂y ∂z
Eletromagnetismo – Departamento de Engenharia Elétrica – Ano 2000
© Prof. João Antônio de Vasconcelos](https://image.slidesharecdn.com/eletro1-090731103718-phpapp02/85/Eletromagnetismo-23-320.jpg)