Curso 2 bb

PROF. OTÁVIO LUCIANO CAMARGO SALES DE MAGALHÃES
2014
CURSO DE
MATEMÁTICA
FINANCEIRA
Para o Concurso do Banco do Brasil - 2014
2ª Turma
S C A R A M O U C H E E D U C A C I O N A L

Prof. Otávio Luciano Camargo Sales de Magalhães | Curso de Matemática Financeira
Fevereiro / 2014 – Banca CESGRANRIO
2
SCARAMOUCHE EDUCACIONAL
CURSO DE MATEMÁTICA COMERCIAL E
FINANCEIRA PARA O CONCURSO DO BANCO
DO BRASIL
(Banca CESGRANRIO)
2ª TURMA – FEVEREIRO/2014
Prof. Ms. Otávio Luciano Camargo Sales de
Magalhães

3
MATEMÁTICA COMERCIAL
Razão e Proporção
1) Em uma competição esportiva participam 500 atletas, sendo 100 moças e 400
rapazes.
a) Qual é a razão entre o número de moças e o número de rapazes?
b) Qual é a razão entre o número de rapazes e o número de moças?
2) Calcule a razão entre:
a) ½ e 5/6 b) -10 e 2 c) 0,05 e 0,65 d) 2/3 e 8/21
3) Calcule a densidade demográfica de uma cidade que tem 435200 habitantes em
170 km2
.
4) Calcule a velocidade média, em km/h de um ciclista que percorre 45 600 metros em
72 minutos.
5) Ache a razão inversa de :
a)
3
7
b)
1
2
3
5
6) Determinar o valor de x de modo que as razões
x
4
3
e
5
6
1
3
sejam inversas uma da
outra.
7) Determinar o valor de x de modo que as razões
x 1
4
e
1
1x 
sejam inversas uma
da outra.
8) Verificar se os números 7, 11, 21 e 27, formam, nessa ordem, uma proporção.
9) Os números 2/3, 1/6, 2 e ½, nessa ordem, formam uma proporção?
10) Determinar o valor de x em cada uma das seguintes proporções:
a)
3
2
7
4x
 b)
4
51
1
17

x
11) Determinar a média geométrica entre os números 12 e 27.
12) A média geométrica entre 0,03 e x é 0,6. Determinar o valor de x.
13) Na proporção x/y=3/5, sendo x+y=48, achar x e y.
14) A largura e o comprimento de um retângulo estão na razão de 4 para 7. Admitindo-
se que o perímetro deste retângulo seja de 66 cm, calcular para esse retângulo:
a) o comprimento e a largura. b) a área.

4
15) Na proporção x/y=7/2, sendo x-y=45, calcular x e y.
16) A diferença de dois lados de um triângulo isósceles é 75 cm, e estão na razão de 8
para 5. Admitindo-se que o lado desigual é o de maior medida, calcular o perímetro
desse triângulo.
17) Dividir 360 em partes proporcionais aos números 2, 3, 4 e 6.
18) As medidas dos ângulos internos de um triângulo são proporcionais aos números
4, 5 e 6. Calcular as medidas dos ângulos internos desse triângulo.
19) Angélica, Áurea e Thaís transportaram de um lugar para outro 156 latas de tinta.
Sabendo-se que Angélica transportou 3 latas de cada vez, Áurea, 4 e Thaís, 6,
pergunta-se: quantas latas transportou cada um?
21) Achar uma fração equivalente a 3/7 cuja soma dos termos seja igual a 50.
22) As medidas dos ângulos internos de um quadrilátero convexo são proporcionais
aos números 3, 4, 6 e 7. Quanto mede cada um dos ângulos, se a soma das medidas
dos ângulos internos de um quadrilátero convexo vale 360º?
23) Achar os valores de x, y e x, admitindo-se que
x y z
x y x
4 3 2
2 3 4 21    e
Divisão Proporcional
1) Dividir o número 32 em partes diretamente proporcionais a 3, 4 e 9.
2) Dividir o número 44 em partes inversamente proporcionais a 6 e 5.
3) Dividindo 660 em partes proporcionais aos números ½, 1/3 e 1/6, obtém-se
respectivamente:
a) 330, 220 e 110 b) 360, 180 e 120 c) 200, 300 e 160
d) 120, 180 e 360 e) 110, 220 e 330
4)(Concurso para Professor de Matemática de 5ª à 8ª séries e Ensino Médio–
Secretaria de Estado da Educação de Minas Gerais/2004) O perímetro de um
triângulo mede 18 metros e seus lados são respectivamente proporcionais a 3, 4 e 5.
Nesse caso, a área desse triângulo mede
a) 12,0 m2
b) 12,5 m2
c) 13,5 m2
d) 14,0 m2
5) (Concurso para Professor de Matemática de 5ª à 8ª séries – Secretaria de
Estado da Educação de Minas Gerais/1993) Dividindo-se 182 em partes
inversamente proporcionais aos números 2, 5 e 6, obtém-se, respectivamente:
a) 80, 62 e 40 b) 90, 50 e 42 c) 100, 32 e 40 d) 105, 42 e 35
e) 110, 35 e 37

5
6) (Exame de Seleção do Centro Estadual de Educação Paula Souza – Ensino
Médio – SP/2º 2003) Como resultado de uma colheita, um agricultor quer dividir a
quantidade de 30.000 castanhas do Pará com seus quatro filhos de idades 18, 22, 26
e 34 anos, de modo que recebam uma parte dessa quantidade diretamente
proporcional às suas idades.
A quantidade que cada um deverá receber, respectivamente, é:
(A) 4.200; 7.000; 8.000; 10.800 (B) 4.600; 7.000; 7.600; 10.800
(C) 5.400; 6.600; 7.000; 11.000 (D) 5.400; 6.800; 7.600; 10.200
(E) 5.400; 6.600; 7.800; 10.200
Médio – SP/1º 2003) Atendendo a suas reivindicações, uma reserva de mata nativa
de 118 km2
foi dividida para preservação da cultura de três comunidades indígenas A,
B e C, em partes inversamente proporcionais a 2, 5 e 7, nesta ordem.
Caberá respectivamente a cada comunidade uma área, em km2
, de:
(A) 50; 40; 28 (B) 50; 48; 20 (C) 60; 38; 20 (D) 70; 38; 10 (E) 70; 28; 20
8) (Olimpíada Paulista de Matemática – 8ª série – 2ª Fase/1982) Os números x, y e
z são diretamente proporcionais aos números 2, 3 e 6. Calcule os valores de x, y e z
sabendo que a diferença entre a diferença de z e y e a diferença entre y e x é 72.
Médio – SP/2º 2002) A abertura de microempresas, grupos autônomos,
associativismo e cooperativismo vem sendo apontada como a grande oportunidade de
as pessoas se desenvolverem na área econômica do empreendedorismo nos dias
atuais. Duas pessoas, A e B, decidiram abrir uma microempresa para fabricação de
pão artesanal. O capital inicial da empresa foi de R$ 4 000,00. A pessoa A entrou com
um capital de R$ 2 500,00 e a pessoa B com um capital de R$ 1 500,00. Ficou
combinado que o lucro seria dividido proporcionalmente ao capital aplicado. No final
do mês o lucro foi de R$ 1 500,00. As parcelas dos lucros que A e B devem receber,
respectivamente, são:
A) R$ 937,50 e R$ 562,50 B) R$ 850,00 e R$ 650,00 C) R$ 715,50 e R$ 784,50
D) R$ 637,50 e R$ 862,50 E) R$ 435,50 e R$ 1 064,50
10) (PUC-MG-2000) Dois sócios participam de um empreendimento em Arcos, um
deles com R$ 5 000,00 e o outro com R$ 3 000,00. No final, obtêm um lucro de R$ 16
000,00. Na divisão proporcional do lucro, o sócio que entrou com R$ 5 000,00 deverá
receber, em milhares de reais:
a) 4 b) 6 c) 8 d) 10 e) 12
11) (UNICAMP-97 / 2ª fase) As pessoas A, B, C e D possuem juntas R$ 2.718,00. S A
tivesse o dobro do que B tem, B tivesse a metade do que tem, C tivesse R$ 10,00 a
mais do que tem e, finalmente, D tivesse R$ 10,00 a menos do que tem então todos
teriam a mesma importância. Quanto possui cada uma das quatro pessoas?
Regra de Sociedade Simples
http://socalculosfinanceiros.blogspot.com.br/2011/07/regra-de-sociedade-simples.html
45) Paulo e Silas entraram numa sociedade comercial, ajustando dividir
proporcionalmente o lucro apurado, segundo a quantia usada na abertura do
comércio. Se o primeiro entrou com R$ 5.000,00 e o segundo com R$ 3.000,00. Se no

6
final do semestre houve um lucro líquido de R$ 2.000,00, quanto caberá para cada
um?
46) Pedro, Tiago e João entraram numa sociedade com valores respectivos de R$
1000,00, R$ 1.500,00 e R$ 2.500,00. No final de 1 ano, obtiveram R$ 15.000,00 de
lucro. Quanto caberá para cada um, se a divisão deve ser proporcional aos valores
que foram usados na formação da sociedade?
47) José e Maria têm, juntos, 80 anos. Sabe-se que o primeiro é mais novo que a
segunda, apenas 10 anos. Resolveram entrar numa sociedade com R$ 100,00. No
final de 1 mês, conseguiram receber apenas R$ 84,00. Se o acordo era dividir o lucro
ou prejuízo proporcionalmente às idades, quanto Maria receberá a mais que José?
48) Anita, Bela, Cida e Doca formaram numa sociedade comercial, ajustando dividir o
lucro ou prejuízo, de acordo com o tempo a que esteve cada uma na sociedade. A
primeira entrou no início de janeiro; a segunda no começo de abril; a terceira no início
de agosto e a quarta no início de outubro. Após um ano que entrou a primeira,
verificaram que tiveram um lucro líquido de R$ 5.800,00. Quanto receberá cada uma?
49) Uma empresa é formada por três sócios: Carla, Eduardo e Vanessa. O segundo é
sócio majoritário, com 51% das ações da empresa. A primeira detém 29% e a terceira
detém o restante das ações. No final de 1 ano, verificou-se um lucro líquido de R$
500.000,00, que serão divididos proporcionalmente a porcentagem das ações. Quanto
receberá Vanessa?
50) A e B entraram numa sociedade, com R$ 500,00 e R$ 1.500,00 respectivamente.
No final de um mês obtiveram R$ 400,00 de lucro. Quanto caberá para cada um, se o
valor deve ser dividido proporcionalmente ao valor de entrada?
51) E, F, G, H e I, formaram uma sociedade comercial e resolveram dividir os R$
9.400,00 de lucro, proporcionalmente ao tempo na sociedade. O primeiro permanecer
2 meses; o segundo, 4 meses; o terceiro, 5 meses; o quarto, 1 ano; e o quinto, 15
dias. Quanto recebeu cada um?
52) J, L e M formaram uma sociedade comercial e resolveram dividir os R$ 350,00 de
prejuízo, proporcionalmente ao tempo na sociedade. O primeiro permanecer 10 dias; o
segundo, 15 dias e o terceiro 1 mês e meio. Quanto pagará cada um de prejuízo?
53) N, P e Q formaram uma sociedade comercial e resolveram dividir os R$ 10.500,00
de lucro, proporcionalmente às idades de cada um. Juntos têm 50 anos, sendo o
segundo mais novo que o terceiro 4 anos e este mais velho que o primeiro 12 anos.
Quanto receberá cada um?
54) Frederico e Diana entraram numa sociedade, com R$ 100,00 e R$ 1.500,00
respectivamente. No final de um mês obtiveram R$ 400,00 de lucro. Quanto caberá
para cada um, se o valor deve ser dividido proporcionalmente ao valor de entrada?
Regra de Sociedade Composta
55) Uma sociedade comercial foi formada com quatro sócios: A, B, C e D. Sabe-se
que o primeiro entrou com R$ 600,00 e permaneceu 3 meses na sociedade. O
segundo entrou com R$ 500,00 e permaneceu 4 meses. O terceiro permaneceu 2
meses e entrou com R$ 400,00 e o quarto entrou com R$ 100,00 e permaneceu 1
mês. Quanto receberá cada um, se a sociedade, no final dos quatro meses, lucrou R$
2.350,00?
segundo entrou com R$ 700,00 e permaneceu 1 mês. O terceiro permaneceu 3 meses
e entrou com R$ 300,00 e o quarto entrou com R$ 800,00 e permaneceu 2 meses.
Quanto receberá cada um, se a sociedade, no final dos cinco meses, lucrou R$
1.050,00?

7
segundo entrou com R$ 350,00 e permaneceu 1 ano. O terceiro permaneceu 3 meses
e entrou com R$ 2.000,00 e o quarto entrou com R$ 1.500,00 e permaneceu 4 meses.
Quanto lucrou a sociedade no final de 1 ano, se o sócio B lucrou R$ 8.400,00?
segundo entrou com R$ 600,00 e permaneceu 1 mês. O terceiro permaneceu 2 meses
e entrou com R$ 150,00 e o quarto entrou com R$ 50,00 e permaneceu 4 meses.
Quanto lucrou a sociedade no final de 4 meses, se o sócio B lucrou R$ 900,00?
segundo entrou com R$ 200,00 e permaneceu 4 meses. O terceiro permaneceu 6
meses e o quarto entrou com R$ 500,00 e permaneceu mês. Quanto lucrou a
sociedade no final de 6 meses, se o sócio C lucrou R$ 1.200,00?
que o primeiro entrou com R$ 1.200,00, permaneceu 4 meses na sociedade e lucrou
R$ 2.400,00. O segundo entrou com R$ 400,00, e permaneceu 2 meses. O terceiro
lucrou R$ 400,00 e o quarto lucrou R$ 500,00. Qual o valor em reais que entrou o
sócio C nesta sociedade, mantendo as mesmas proporções?
que o primeiro entrou com R$ 300,00 permaneceu 2 meses na sociedade e lucrou R$
60,00. O segundo entrou com R$ 400,00. O terceiro permaneceu 3 meses e o quarto
entrou com R$ 300,00. Sabe-se ainda que os quatro sócios, juntos, entraram com R$
1.400,00. Qual o valor em reais que lucrou o sócio C nesta sociedade, mantendo as
mesmas proporções?
que o primeiro entrou com R$ 300,00. O segundo entrou com R$ 200,00 e lucrou R$
400,00. O terceiro, com R$ 400,00. O quarto permaneceu durante 2 meses e lucrou
R$ 400,00. Se os juntos, entraram com R$ 1.100,00, quantos meses passou o
segundo sócio nesta sociedade?
63) Uma sociedade foi formada com cinco sócios: A, B, C, D e E. O primeiro
permaneceu 1 mês e lucrou R$ 2.100,00; o segundo entrou com R$ 450,00; o terceiro
entrou com R$ 650,00, permaneceu 2 meses e lucrou R$ 3.900,00. O quarto
permaneceu 3 meses e o quinto entrou com R$ 300,00. Se juntos entraram com R$
2.300,00, quanto lucrou o sócio D?
64) Uma sociedade foi formada com cinco sócios: A, B, C, D e E. O primeiro entrou
com R$ 450,00; o segundo permaneceu 1 mês e lucrou R$ 2.100,00; o quarto entrou
com R$ 650,00, permaneceu 2 meses e lucrou R$ 3.900,00; o quinto entrou com R$
300,00. Se juntos, entraram com R$ 2.300,00, quanto tempo permaneceu o terceiro,
se este lucrou R$ 1.800,00?
com R$ 120,00 e lucrou R$ 40,00; o segundo entrou com R$ 60,00, permaneceu 3
meses e lucrou R$ 60,00; o terceiro entrou com R$ 70,00; o quarto entrou com R$
60,00 e lucrou R$ 60,00; o quinto entrou com R$ 90 e permaneceu 2 meses. Quanto
tempo permaneceu o sócio C, se toda a sociedade lucrou R$ 290,00?
com R$ 10,00, permaneceu 1 ano e lucrou R$ 240,00; o segundo permaneceu 3
meses e lucrou R$ 1.200,00; o terceiro permaneceu 15 dias e lucrou R$ 400,00; o
quarto permaneceu 10 dias; o quinto permaneceu 1 semestre e lucrou R$ 72,00. Se
juntos, lucraram R$ 1.926,00, qual o total do capital inicial desta sociedade?
com R$ 200,00 e permaneceu 1 ano; o segundo entrou com R$ 700,00, permaneceu 3
anos e lucrou R$ 8.400,00; o terceiro permaneceu 1 semestre e lucrou R$ 200,00; o
quarto entrou com R$ 300,00 e permaneceu 5 anos. Se juntos entraram com R$
2.300,00 e juntos lucraram R$ 16.000,00, quanto tempo permaneceu o quinto sócio?

8
68) Uma sociedade foi formada com cinco sócios: A, B, C, D e E. O primeiro
permaneceu 2 meses e lucrou R$ 400,00; o segundo permaneceu 1 mês e lucrou R$
350,00; o terceiro entrou com R$ 300,00 e permaneceu 3 meses; o quarto entrou com
R$ 600,00, lucrou R$ 300,00 e permaneceu 1 mês; se juntos, entram com R$ 5.000,00
e lucraram juntos R$ 1.600,00, quanto permaneceu o sócio E, se este entrou com R$
3.000,00?
Regra de Três Simples
1) Em dois dias, ando 50 km. Quantos km eu ando em meio dia?
2) Gastei R$ 150,00 na compra de 3 mercadorias. Se desejo comprar 2,5 mercadorias,
quanto terei que gastar?
3) Trabalhando 5 horas por dia, faço 80 metros de uma estrada por dia. Quantas horas
eu terei que trabalhar por dia, para fazer 20 metros a mais de uma mesma estrada?
4) Faço um determinado serviço em 15 dias, trabalhando 8 horas diárias. Se outra
obra semelhante foi concluída em 20 dias, quantas horas eu trabalhei a menos por
dia?
5) Em um tanque há duas torneiras. A primeira enche-o em 4 horas e a segunda,
esvazia-o em 12 horas. Abrindo-se as duas torneiras ao mesmo tempo e estando o
tanque vazio, em quantas horas ficará cheio?
6) A produção de uma tecelagem era de 8.000 m de tecido por dia. Com a admissão
de mais 300 operários, a indústria passou a produzir 14.000 m de tecido por dia. Qual
era o número de operários antes da admissão dos 300?
7) (TTN-92) Uma pessoa caminha com passadas iguais de 80 cm, com velocidade
constante de 2 m/s. Quantos passos ela dará em 60 s?
8) Três torneiras completamente abertas enchem um tanque em 11 horas e 30
minutos. Quantas torneiras de mesma vazão seriam necessárias para encher o tanque
em 54 minutos?
9) Trabalhando-se 6 horas diárias, faço um serviço em 10 dias. Em quantos dias farei
outro serviço semelhante, trabalhando 2 horas a menos por dia ?
10) Com 15 faço 6; 15 faço com . . .
Regra de Três Composta
Principais Métodos:
* Flechas
* Redução à Unidade
* Causa e Efeito
1) Sabe-se que 5 pessoas, durante 2 dias fazem 10 objetos. Quantos objetos 4
homens farão, trabalhando-se 3 dias a mais?
2) Se 10 homens, durante 8 dias, trabalhando 6 horas diárias fazem 1.500 metros de
uma estrada, quantos homens serão necessários para se fazer 2.000 metros de uma
estrada de tamanha dificuldade, se desta vez, o serviço tem que ser concluído em 3
dias a menos, onde os operários trabalham 8 horas diárias?
3) Sabe-se que 20 homens, durante dois dias, fazem 50 metros de uma estrada. Uma
outra turma de 4 homens, farão 5 metros de uma Segunda estrada em quantos dias,
sabendo-se que a estrada da segunda turma é três vezes mais complicada que a
primeira?
4) Cinco indústrias, com um total de 150 homens cada, produzem 200 carros em um
determinado período. Uma indústria, com 100 homens, fará quantos carros na décima
parte do tempo levado pelas cinco indústrias anteriores, se o coeficiente de dificuldade
desta vez é menor 4 vezes?
5) Quatro operários, trabalhando 5 horas diárias, durante 8 dias, levantam um muro de
quatro metros de altura por 10 metros de comprimento e meio metro de largura.
Quanto metros cúbicos de um outro muro fará 1 homem, trabalhando durante 15 dias,
6 horas diárias?

9
6) Três operários, trabalhando durante 6 dias, produzem 400 peças. Quantas peças
desse mesmo tipo produzirão sete operários, trabalhando 9 dias?
7) Um ciclista percorre 120 km em 2 dias, dirigindo 3 horas por dia. Em quantos dias
percorrerá 500 km, viajando 5 horas por dia?
8) Uma placa de chumbo de 8 cm de comprimento e 6 cm de largura pesa 96 U.P.
(unidade de peso). Quanto pesará outra placa do mesmo material e da mesma
espessura, só que quadrada, com 10 cm de lado?
9) Numa fazenda, três cavalos consomem 210 kg de alfafa durante sete dias. Para
alimentar 8 cavalos durante 10 dias, quantos quilos de alfafa serão necessários?
10) Se 20 operários levam 10 dias para levantar um muro de 2 metros de altura e 25
metros de comprimento, quantos dias levarão 15 operários para construir um outro, da
mesma largura, mas com 3 m de altura e 40 m de comprimento?
Porcentagem
Poderíamos falar muito sobre porcentagem e apresentar uma série enorme de
problemas e exemplos sobre porcentagens.
Porém, vamos deixar isto por conta do leitor interessado no assunto. Não
entraremos em detalhes das inúmeras regras que podem ser utilizadas para resolver
cálculos de porcentagem (regra de três, cálculos aritméticos, equações, fórmulas,
calculadora, tabelas). Poderíamos falar bastante sobre porcentagem: lucro, desconto,
porcentagem por dentro e por fora, abatimentos e descontos sucessivos, etc... Porém,
acreditamos que quase tudo de porcentagem pode ser feito na base da intuição,
baseando-se em conhecimentos.
Faremos, porém, algumas observações
a) Uso da calculadora:
(i) achar a porcentagem de um determinado valor. Ex: 20% de 100
digite: 100 x 20 % (não aperte o sinal de =)
(ii) fazer um acréscimo sobre um valor. Ex: ache o preço de um produto de R$
100,00 com um acréscimo 30%.
digite: 100 + 30 % (não aperte o sinal de =)
(iii) dar um desconto no preço de um produto. Ex: um produto custa R$ 100,00,
dei um desconto de 15%.
digite 100 – 15 % (não aperte o sinal de =)
(iv) tendo um valor e a porcentagem, determinar o total. Ex: 100 é 40% de
quanto?
digite 100  40 % (não aperte o sinal de =)
b) Acréscimos e descontos
Observe os fatos:
(i) Fazer um acréscimo de 20% de depois outro de 30% não é fazer
acréscimo de 50%, mas de 56%.

10
Veja só: 100 reais mais 20% é 120. Se fizermos um acréscimo de 30%,
estamos fazendo um acréscimo sobre 120 e não sobre 100, ou seja, 30%
de 120 é 36, portanto, o novo valor é 156, 56% a mais que 100.
Para fazer os cálculos é fácil. Basta pegar o valor 120.120%.130%
(acréscimo de 20% significa multiplicar o valor por 120%) ou
120.1,2.1,3=120.1,56.
(ii) Se fizermos um acréscimo de 20% de depois darmos um desconto do
mesmo valor não vamos ficar com o valor original.
Veja só: 100 reais mais 20% é 120. Se descontarmos 20%, vamos
descontar 24 reais, ou seja, ficaremos com 96 reais.
(iii) Desinformados sobre as sutilezas das porcentagens podem ser facilmente
enganados. Por exemplo, podemos encarar 20% de 120 de duas formas:
 Porcentagem “por dentro”, ou seja, 120,00 é o total, 20% é 24.
 Porcentagem “por for”, ou seja, 120,00 é o total mais 20%, ou seja 120%,
portanto, podemos considerar os 20% como 20.
Geralmente é usada a porcentagem “por dentro”, mas, em alguns casos costuma-se
usar, muitas vezes para tirar proveito, a porcentagem “por fora”.
EXERCÍCIOS PROPOSTOS
1) Calcular 30% de 80%
2) Sobre uma compra de R$ 37,00 foi concedido um abatimento de R$ 7,40. Qual foi a
taxa porcentual do desconto sobre o preço da compra?
3) Em um concurso estão inscritos 275 candidatos, dos quais, apenas 176 são
homens. Qual a taxa porcentual de mulheres inscritas?
4) Um comerciante vendeu uma certa mercadoria por R$ 27,75, correspondendo a
75% do preço de tabela. Qual é o preço de tabela dessa mercadoria?
5) Uma certa peça de um carro, cujo preço era de R$ 175,00 foi vendida com um
acréscimo de 20% sobre esse preço de tabela. Qual era o preço de tabela dessa
mercadoria?
6) Um relógio avaliado em R$ 85,00 foi vendido com um desconto de 10% sobre esse
preço. Qual foi o preço de venda?
7) Uma jóia cujo preço de custo era de R$ 7200,00 foi vendida por R$ 8640,00. De
quantos por cento foi o lucro sobre o preço de custo?
8) Uma certa mercadoria vendida por R$ 450,00 apresentou um lucro de R$ 90,00. De
quantos por cento foi o lucro sobre o preço de venda?
9) Um rádio vendido por R$ 360,00 deu um lucro de 30% sobre o preço de venda.
Qual era o preço de custo desse rádio?
10) Determinar de quantos por cento sobre o custo é o lucro de 20% sobre a venda.
11) Uma certa mercadoria que custa R$ 84,00 é vendida com um prejuízo de 20%
sobre o preço de venda. Qual é o preço de venda dessa mercadoria?
12) Uma certa mercadoria é vendida com o prejuízo de 20% sobre o preço de venda.
Sendo o prejuízo de R$ 140,00, calcular o preço de custo.

11
13) Uma certa mercadoria de preço inicial de R$ 450,00 é vendida com os aumentos
sucessivos de 18% e 20%. Qual o último preço de venda?
14) (FUVEST) Atualmente 50% das gaivotas de certa região são brancas e 50% são
cinzentas. Se a população da espécie branca aumentar 40% ao ano e a da espécie
cinzenta aumentar 80% ao ano, qual será, aproximadamente, a porcentagem de
gaivotas brancas daqui a dois anos?
a) 50% b) 38% c) 26% d) 14% e) 9%
15) Uma certa mercadoria custa R$ 60,00 e é vendida com os descontos sucessivos
de 20% e 15%. Qual o segundo preço de venda?
16) A cada mês que passa, o valor de uma certa mercadoria desvaloriza 40% em
relação ao seu valor anterior. O valor dessa mercadoria no primeiro mês é R$ 250,00.
Qual o valor dessa mercadoria no quinto mês?
17) Calcular:
a) 38% de 60% b) 24% de 135%
18) (FUVEST) (10%)2
a) 100% b) 20% c) 5% d) 1% e) 0,1%
19) Em um jantar de 16 convidados, faltam 3. Qual a taxa porcentual de ausentes?
20) Uma certa mercadoria cujo preço era R$ 125,00, foi vendida com um desconto de
R$ 20,00. Qual é a taxa porcentual do desconto sobre o preço inicial?
21) Em uma sala de aula de 150 alunos, somente 144 estão presentes. Qual é a taxa
porcentual de ausentes?
22) Um exército de 15000 soldados perdeu em um combate exatamente 1 200
combatentes. Qual a taxa porcentual dos sobreviventes em relação ao exército?
23) Uma pessoa vendeu um automóvel por 70% do preço de mercado. Sabendo-se
que ele recebeu a importância de R$ 245 000,00 pela venda, qual é o preço de
mercado desse carro?
24) Em uma competição esportiva participaram rapazes e moças. Sabe-se que 34%
dos participantes são moças e 1650 são rapazes. Quantos atletas participaram dessa
competição?
25) Uma certa jóia, cujo preço era de R$ 125 000,00, foi vendida com um acréscimo
de 40% sobre esse preço. Qual foi o preço de venda?
26) Um retângulo tem área de 250 m2
. Se um lado deste retângulo é acrescido de
16%, obter a área desse outro retângulo.
27) Uma jóia é avaliada em R$ 3390,00 e vendida com um desconto de 20%, sobre
esse preço. Qual é o preço de venda dessa jóia?
28) Um automóvel cujo preço é R$ 136 000,00 foi vendido com um prejuízo de 25%
sobre esse preço. Qual é o preço de venda?

12
29) Um iate foi vendida por R$ 1 064 000,00. De quantos porcento foi o lucro sobre o
preço de custo, que era R$ 950 000,00.
30) (FUVEST) Uma certa mercadoria, que custava R$ 12,50, teve um aumento,
passando a custar R$ 13,50. A majoração sobre o preço antigo foi de:
a) 1,0% b) 10,0% c) 12,5% d) 8,0% e) 10,8%
31) Um livro vendido por R$ 120,00 deu um lucro de R$ 36,00 sobre o preço de venda.
De quantos por cento foi o lucro?
32) Uma máquina fotográfica foi vendida por R$ 950,00, dando um lucro de R$ 114,00.
Qual é a taxa porcentual do lucro sobre o preço de venda?
33) Calcular o preço de custo de um uniforme escolar que, vendido por R$ 1600,00,
deu um lucro de 15% sobre o preço de venda.
34) Uma geladeira vendida por R$ 85 000,00 deu um lucro de 20% sobre o preço de
venda. Qual era o preço de custo dessa geladeira?
35) Determinar de quantos por cento sobre o custo é o lucro de 75% sobre a venda.
36) (FUVEST) Um vendedor ambulante vende seus produtos com um lucro de 50%
sobre o preço de venda. Então seu lucro sobre o preço de custo é de:
a) 10% b) 25% c) 33,333...% d) 100% e) 120%
37) Uma televisão que custou R$ 2860,00 foi vendida com um prejuízo de 10% sobre
o preço de venda. Qual foi o preço de venda?
38) Determinar de quantos por cento sobre o custo é o prejuízo de 100% sobre a
venda.
39) Um comerciante vendeu um rádio com o prejuízo de R$ 400,00, correspondente a
10% sobre a venda. Qual o custo desse rádio?
40) Um vendedor teve um prejuízo de R$ 250,00, equivalentes a 16% sobre a venda
de uma mercadoria. Qual o preço de custo?
41) Uma certa mercadoria foi comprada e revendida sucessivamente por dois
negociantes. O primeiro obteve um lucro de 10% sobre o respectivo preço de compra.
O segundo a negociou sofrendo um prejuízo de 10% sobre o respectivo preço de
compra. Calcular o preço pelo qual o primeiro a adquiriu, sabendo que o segundo a
transferiu ao comprador por R$ 2079,00.
42) (FUVEST) O preço de certa mercadoria sofre anualmente um acréscimo de 100%.
Supondo que o preço atual seja de R$ 100,00 daqui a três anos o preço será:
a) R$ 300,00 b) R$ 400,00 c) R$ 600,00 d) R$ 800,00 e) R$ 1000,00
43) (FUVEST) No dia 1º de Setembro, foi aberta uma caderneta de poupança e
depositada uma quantia x. No dia 1º de dezembro do mesmo ano o saldo era de Cr$
665 500,00. Sabendo que, entre juros e correção monetária, a caderneta rendeu 10%
ao mês, qual era a quantia x, em milhares de cruzeiros?
a) 650 b) 600 c) 550 d) 500 e) 450

13
44) (FUVEST) Um país contraiu em 1829 um empréstimo de 1 milhão de dólares, para
pagar em cem anos à taxa de juros de 9% ao ano. Por problemas de balança
comercial, nada foi pago até hoje, e a dívida foi sendo “rolada”, com capitalização
anual de juros. Qual dos valores abaixo está mais próximo do valor da dívida em
1989? Para os cálculos adote (1,09)8
=2.
a) 14 milhões de dólares b) 500 milhões de dólares
c) 1 bilhão de dólares d) 80 bilhões de dólares e) 1 trilhão de dólares
45) Um produto cosmético que custa R$ 400,00 é vendido com os descontos
sucessivos de 15%, 10% e 20%. Qual o último preço de venda?
46) (FUVEST) A cada ano que passa, o valor de um carro diminui 30% em relação ao
seu valor anterior. Se v for o valor do carro no primeiro ano, o seu valor no oitavo ano
será:
a) (0,7)7
.v b) (0,3)7
.v c) (0,7)8
.v d) (0,3)8
.v e) (0,3)9
.v
47) (FUVEST) Uma certa mercadoria é vendida nas lojas A e B, sendo R$ 20,00 mais
cara em B. Se a loja oferecesse um desconto de 10%, o preço nas duas lojas seria o
mesmo. Qual o preço na loja A?
48) (FUVEST) Numa certa população, 18% das pessoas são gordas, 30% dos homens
são gordos e 10% das mulheres são gordas. Qual a porcentagem de homens na
população?
49) (FUVEST) Uma empresa que produz um único artigo está procurando determinar
o volume de vendas (em cruzeiros) para o mês de março de 1977, para que seu lucro
neste mês represente 30% do total das vendas. Para produzir tal artigo, a empresa
tem dois tipos de despesas: uma despesa fixa e uma despesa variável. A despesa fixa
foi estimada em Cr$ 120 000,00, enquanto a despesa variável deverá ser igual a 40%
do total das vendas. Qual o volume de vendas que realiza as expectativas do
empresário?
50) (UNICAMP) Um fabricante de televisores oferece como “vantagem” a devolução
do dinheiro pago pelos seus produtos dois anos após a compra. Sabe-se que com
uma inflação anual de 900% os preços das mercadorias sobem ,em um ano, dez
vezes o seu valor original. Supondo uma inflação anual de 900% nesses dois anos, se
ao invés de devolver o dinheiro o fabricante desse, no ato da compra, um desconto
equivalente ao dinheiro a ser devolvido, de quanto por cento deveria ser esse
desconto?
Juros Simples
http://socalculosfinanceiros.blogspot.com.br/2011/07/regra-de-sociedade-simples.html
112) Quanto rende de juro simples um capital de R$ 500,00, empregado a uma taxa
de 3% aa, durante 5 anos?
113) Quanto rende de juro simples um capital de R$ 700,00, empregado a uma taxa
de 5% aa, durante 2,5 anos?
114) Quanto rende de juro simples um capital de R$ 8.000,00, empregado a uma taxa
de 2,5% aa, durante 6 meses?

14
de 1% am, durante 1 ano?
de 2,03% at, durante 3 quadrimestres?
122) Qual o capital, no regime de juros simples, que empregado a uma taxa de 3% aa,
rende, em 2 anos, R$ 120,25?
125) Qual o capital, no regime de juros simples, que empregado a uma taxa de 0,98%
am, rende, em 1 trimestre, R$ 98,45?
126) Sabe-se que R$ 350,00 aplicados durante um prazo de 2 meses, renderam R$
35,00 de juro simples. Qual a taxa mensal utilizada?
127) Sabe-se que R$ 180,00 aplicados durante um prazo de 1 semestre, renderam R$
128) Sabe-se que R$ 300,00 aplicados durante um prazo de 75 dias, renderam R$
129) Sabe-se que R$ 900,00 aplicados durante um prazo de 1 semestre, renderam R$
54,00 de juro simples. Qual a taxa anual utilizada?
130) Durante quantos meses, um capital de R$ 350,00, aplicado a uma taxa 5% am,
rende R$ 35,00 de juro simples?
133) Durante quantos meses, um capital de R$ 900,00, aplicado a uma taxa 12% aa,
rende R$ 54,00 de juro simples?
134) Ivo aplicou um capital por 3 meses, à taxa de juro simples de 7% am. Decorridos
os três meses, o mesmo capital inicial foi aplicado por mais dois meses, à taxa de 48%
aa. A soma do juro simples obtido nas duas transações foi de R$ 36.250,00. Qual foi o
capital inicial aplicado?
135) Fiz uma aplicação de R$ 300.000,00, esperando que o dinheiro rendesse à taxa
de 60% aa. No entanto, após certo período de tempo, a taxa foi reduzida a 4% am.
Qual o prazo em que vigorou a 2a taxa se, após 10 meses, o capital rendeu R$
141.000,00 de juro simples?
136) Qual o montante produzido por uma de capital de R$ 250,00, aplicado a uma taxa
de 5% am, durante 2 meses, no regime de juros simples?
137) Qual o montante produzido por um capital de R$ 500,00, aplicado a uma taxa de
1,3% am, durante 4 meses no regime de juros simples?
139) Uma empresa tomou emprestada a quantia de R$ 451.000,00, comprometendo-
se a liquidar a dívida em 45 dias, pagando por esta R$ 572.770,00. Qual a taxa
mensal de juro simples adotada nessa operação?
143) Uma pessoa aplicou um certo capital em um banco, à taxa de juro simples de
96% aa. Transcorridos 5 meses, essa pessoa retirou o capital mais juro e aplicou-os
em um outro banco, por 3 meses, à taxa de juro simples de 9% am, obtendo com isso
um juro de R$ 4.536,00. Qual o capital inicial aplicado por essa pessoa?

15
144) (Receita Federal) Paulo Colocou R$ 200.000,00 à taxa de juro simples de 96%
aa, pelo prazo de 10 meses. Entretanto, antes do término do prazo, conseguiu um
aumento da taxa de juro para 144% aa, referente ao restante do prazo. Sabendo-se
que no final do período recebeu um montante de R$ 376.000,00, o tempo em que o
capital esteve aplicado a taxa menor foi de:
145) (Petrobrás) Uma loja vende um determinado objeto por R$ 10.500,00 à vista. Na
venda desse aparelho, a prazo, a loja acresce ao preço à vista 15% deste, e este total
é dividido em duas prestações, sendo a primeira paga no ato da compra e a segunda
após 1 mês. Qual a taxa de juro simples relativa a essa operação?
146) Uma loja oferece um aparelho por R$ 500,00, à vista. Na compra desse aparelho
a prazo, pede-se 20% do valor à vista, como entrada, e mais um pagamento de R$
550,00 no prazo de 2 meses. Que taxa de juro simples a loja está cobrando nessa
operação?
147) Uma loja vende um aparelho de som por 1.800,00 à vista. A prazo, o aparelho é
vendido por R$ 2.016,00, sendo R$ 360,00 de entrada e o restante pago após 45 dias.
Qual a taxa mensal de juro simples adotada nessa operação?
Juros Compostos
188) Um investidor aplicou a quantia de R$ 300.000,00, à taxa de juro composto de
7% am. Que montante este capital irá gerar após 5 meses?
189) Calcular o juro composto que se obterá na operação de R$ 100.000,00, a 15%
aa, durante 48 meses.
190) Um capital de R$ 10.000,00 esteve aplicado por 4 meses e gerou um montante
de R$ 12.155,06. A que taxa esteve aplicado?
191) Durante quanto tempo deve ficar aplicado o capital de R$ 35.000,00, à taxa
composta de 10% am, para que o mesmo produza juro de R$ 11.585,00?
192) O capital de R$ 25.000,00 foi aplicado a juro composto de 3% am. Qual o
montante no final de 3 anos e 8 meses?
193) Uma pessoa aplicou, em caderneta de poupança, a quantia de R$ 300.000,00
por 3 meses. Qual o seu saldo no fim desse prazo, se o rendimento do dinheiro
nesses meses deu-se com base nas taxas de 1,2%, 1,5% e 1%?
194) Tomei emprestados R$ 150.000,00 pelo prazo de 4 meses, comprometendo-me
a pagar juro com base nas taxas de inflação de cada período. Quanto pagarei de juro,
se as taxas de inflação de cada período foram, respectivamente 7%, 5,5%, 4% e 5%?
195) Um agiota emprestou a uma pessoa a quantia de R$ 100.000,00 pelo prazo de 5
dias, exigindo por esse empréstimo o pagamento de R$ 15.927,40 de juro. Que taxa
diária de juro composto o agiota está cobrando?
196) Com a finalidade de comprar um carro que custa R$ 42.076,56, uma pessoa fez
uma aplicação de R$ 30.000,00 em um banco que paga 7% am de juro composto.
Quanto tempo levou essa aplicação para atingir o valor desejado?

16
197) Qual o montante produzido por um capital de R$ 300,00, sob o regime de juro
composto, aplicado a uma taxa de 1,006% am, durante um prazo de 1 ano?
198) Após 2 anos, sob uma taxa composta de 0,5% am, qual o montante produzido
por um capital de R$ 15.000,00?
199) Teodorico emprestou R$ 5.000,00 a um colega de trabalho, a uma taxa composta
de R$ 2% am, pelo prazo de 5 meses e quinze dias. Qual o valor que ele deve receber
no final deste período?
200) Um certo capital, investido sob o regime de juro composto, a uma taxa de 1% ab,
durante 8 meses, com capitalização mensal, geral um montante de R$ 260,18. Qual o
valor desse capital?
201) Um certo capital, investido sob o regime de juro composto, a uma taxa de 3% at,
durante 8 meses, com capitalização bimestral, geral um montante de R$ 5.000,00.
Qual o valor desse capital?
202) Uma pessoa investiu em um banco R$ 150.000,00, à taxa composta de 10% am,
por 140 dias. Qual o montante relativo a essa aplicação?
203) Por quanto tempo deve-se aplicar um capital de R$ 10.000,00, à taxa composta
de R$ 5% am, para obter-se, no final do prazo, um montante de R$ 14.489,01?
204) O preço de um objeto é R$ 1.200,00, podendo esse valor ser pago daqui a 3
meses. Na compra desse objeto, à vista, dá-se um desconto de 15%. Qual a taxa de
juro composto envolvida nessa operação?
205) Um objeto custa, à vista, R$ 2.000,00. Na compra a prazo, dá-se R$ 700,00 de
entrada e mais um pagamento de R$ 1.500,00 para 60 dias. Qual a taxa mensal de
juro composto envolvida nessa operação?
206) Que taxa mensal de juro composto é recebida por um investidor que aplicou R$
50.000,00 e resgatou após 8 meses, a quantia de R$ 92.546,50?
Desconto Simples
DESCONTOS SIMPLES
Há dois tipos
DESCONTO BANCÁRIO, COMERCIAL, OU ‘POR FORA’ – incide sobre o
valor NOMINAL
DESCONTO RACIONAL, OU ‘POR DENTRO’ – incide sobre o valor LÍQUIDO
Utilizamos os seguintes conceitos
D – desconto N – valor nominal L – valor líquido (N-D) i – taxa
t – tempo
DESCONTO BANCÁRIO - D=N.i.n
DESCONTO RACIONAL – D=L.i.n
1) Qual é o desconto que deverá incidir sobre um título de R$ 750,00, pago 2 meses e
10 dias antes do vencimento, com uma taxa de 5% ao mês?
2) Um título no valor de R$ 1.200,00, pago 5 meses antes do vencimento, ficou
reduzido a R$ 900,00. Qual foi a taxa mensal utilizada?

17
3) Resgatei, em 16 de abril, uma nota promissória com vencimento marcado para 10
de junho do mesmo ano. Obtive um desconto de R$ 4.400,00, calculado com uma taxa
mensal de 6%. Qual era o valor mensal da promissória?
4) Calcule o desconto por dentro de um título de R$ 6.864,00, a uma taxa de 12% ao
mês, pago 1 mês e 6 dias antes do vencimento.
5) Um título com valor nominal de R$ 2.000,00, a uma taxa de 3% ao mês, vai ser
descontado 8 meses antes do vencimento. Calcular a diferença entre os descontos
bancário e racional.
6) Calcular a taxa a ser aplicada, num desconto por dentro, em uma duplicata de R$
1.200,00, de modo que dois meses e meio antes do vencimento ela se reduza a R$
1.000,00.
Desconto Composto
N=Va.(1+i)t
, sendo Va o valor que será pago.
1) Calcular o valor atual de um título de R$ 12.000,00, à taxa de 9% a.m., disponível
em 8 meses.
2) Calcular os três tipos de desconto possíveis para um título de R$ 9.000,00, à taxa
de 5% ao mês, resgatado 5 meses antes do vencimento.
3) Uma duplicata no valor de R$ 120.000,00 e com vencimento em 4 anos, por quanto
será paga hoje se sofrer um desconto composto de 14% a.a.?
4) Que taxa de desconto composto sofreu um título de R$ 20.000,00 que, pago 5
meses antes do prazo, foi reduzido a R$ 14.950,00?
Taxas
TAXAS EQUIVALENTES
(1+id)360
=(1+im)12
=1+ia
TAXA EFETIVA
É a taxa quando coincide com a unidade de tempo do período de capitalização
TAXA NOMINAL
É a taxa que o tempo não coincide com o tempo de capitalização
1) Calcule a taxa mensal equivalente a 36% ao ano.
2) Calcule a taxa anual equivalente a 3% ao mês.
3) Calcule a taxa trimestral equivalente a 12% ao semestre
4) Calcular o montante de uma aplicação de R$ 8.500,00 a juros compostos, à taxa de
3,5% ao mês, capitalizado mensalmente durante 9 anos.
5) Calcular o montante de uma aplicação de R$ 42.000,00, a juros compostos,
capitalizado mensalmente, à taxa de 42% ao ano, durante 3 anos e 4 meses.

18
6) Quanto devemos aplicar, no regime de juros compostos, capitalizado anualmente, à
taxa de 36% ao ano, para obtermos em 2 anos, 3 meses e 20 dias a importância de
R$ 436.837,42?
7) Quanto devemos aplicar à taxa de 2,5% ao mês, no regime de juros compostos,
para obtermos em 1 ano e 4 meses a importância de R$ 200.000,00?
8) Em que prazo a quantia de R$ 120.000,00, a 4% ao mês, renderá de juros
compostos a importância de R$ 90.535,71?
9) A quantia de R$ 500.000,00 foi colocada a juros compostos durante 8 meses e
rendeu R$ 267.343,26 de juros. Calcular a taxa mensal dessa aplicação.
10) A que taxa mensal foi empregada a juros compostos, a importância de R$
180.000,00 para acumular em 6 meses e 20 dias o montante de R$ 230.810,13?
11) Uma loja de eletrodomésticos financia as mercadorias que vende. A taxa de juros
é de 42% ao ano, capitalizados mensalmente. Qual é, neste caso, a taxa anual
efetiva?
12) Complete a tabela com as taxas efetivas correspondentes a taxa nominal de 36%
ao ano.
Período de Capitalização Taxa Efetiva
Anual
Semestral
Trimestral
Bimestral
Mensal
13) Colocar dentro dos quadros da tabela a seguir as taxas efetivas equivalente às
taxas nominais indicadas na primeira coluna.
Taxa
Nominal
(anual)
Taxas Efetivas Equivalentes
anual semestral trimestral mensal diária
20%
36%
42%
54%

19
MATEMÁTICA FINANCEIRA
Observações sobre o uso da calculadora financeira HP-12C
Noções Básicas
A Calculadora HP-12C é muito antiga, possui quase 30 anos, porém, pelo uso
e costume continuou a ser utilizada para cálculos financeiros, apesar de existirem
novos modelos, muito mais modernos e fáceis de serem utilizados.
A Calculadora HP-12C hoje é fabricada em novos modelos, mais modernos, na
versão Prestige e Platinum. Ela foi consolidada pelo uso.
O modo tradicional de uso da calculadora (único na versão original) é o Método
Polonês Reverso (VPN), que facilita os cálculos, mas não é o modo que estamos
acostumados.
Só para exemplificar, vamos fazer o cálculo de 5+3
 No método tradicional. Pressionamos a tecla 5, a tecla +, a tecla 3, e a tecla =.
 No Método Polonês Reverso. Pressionamos a tecla 5, a tecla ENTER, a tecla
3, a tecla ENTER e o sinal +.
Note que a HP 12C não tem a tecla de =.

20
Em geral, calculadoras só possuem 2 funções por botão, sendo acionada a 2ª
função por uma tecla geralmente chamada SHIFT ou 2ndF.
A HP 12C possui 3 funções por botão, possuindo duas teclas “SHIFT”:
Essas teclas possuem nomes de “f” e “g” e aparecem na cor dourada (ou
laranja) e azul. A função “f” é chamada de função dourada ou segunda função, a
função “g” é chamada de função azul.
A tecla que tem a função principal FV (montante) possui segunda função IRR e
terceira função Nj.
Funções Financeiras básicas
A HP 12C tem como funções financeiras principais:
n = tempo
i = taxa
PV = Present Value (valor presente, o Capital)
PMT = Payment Amount Temporary (pagamento do montante temporário – as
parcelas)
FV = Future Value (valor futuro, o montante)
Observando os fluxos de caixa, vemos que o VP (que é o PV na calculadora)
ou o VF (que é o FV) possuem “sentidos” opostos, portanto, é preciso digitar na
calculadora esses valores com sinal contrário das PMT e do tempo e taxa.
Portanto, sempre é preciso mudar o sinal desses, usando a tecla CHS, que
equivale a tecla +/- das calculadoras comuns.

21
Além disso, no Brasil, usa-se o método de juros contínuo. A HP 12C é
programada para calcular períodos inteiros com juros compostos, e períodos
fracionários com juros simples. Portanto, se o tempo for fracionário, é necessário
colocar no modo contínuo, digitando em seqüência STO e EEX
Aparecerá um “C” no visor.
Não há problemas se deixar o “C” o tempo inteiro. Porém, é necessário caso o
tempo seja fracionário. (Convenção Linear X Convenção Exponencial)
Antes de fazer qualquer cálculo é também importante limpar os registradores,
pressionando ‘f’ e REG.
Apertar apenas CLX não garante que os dados foram retirados do cálculo a ser
efetuado. O CLX limpa apenas o que está no visor.
Supondo já estar com o “C” no visor, e limpo os registradores com o REG,
devemos digitar os valores que possuímos e apertar o que desejamos encontrar.
Veja os exemplos:
Exemplo 1: Quanto deverá receber uma pessoa que empresta $ 500,00 por 5 meses
à taxa de 3% ao mês?
500 CHS PV
5 n
3 i
FV
Você obterá o valor do montante FV
Exemplo 2: Calcule a taxa de juros correspondente a uma aplicação de $ 1.000,00
por 10 meses e valor de resgate $ 1.280,08
1000 CHS PV
1280,08 FV
10 n
I
Não esqueça, antes de cada cálculo, pressione f REG.
A calculadora HP 12C faz cálculos com juros simples, porém, essas teclas básicas
sempre calcularão no regime de juros compostos.
Financiamento e Aplicações

22
PROBLEMA GERADOR
Você deseja comprar um aparelho eletrônico, e, para isso começa a pesquisar em
várias lojas pela Internet. Você percebe que não será possível comprá-lo a vista,
porém, percebe duas ofertam aparentemente interessantes.
 A Loja A está vendendo o aparelho por R$ 550,00 a vista ou em 10 parcelas
iguais e mensais de R$ 59,64, o primeiro 30 dias após a compra.
 A Loja B vende o mesmo aparelho por R$ 550,00 a vista ou em 12 parcelas
iguais e mensais de R$ 49,94, sendo o primeiro pagamento feito no ato da
compra (entrada).
Qual das alternativas é mais vantajosa?
Adaptado de:
http://lojavirtual.bmf.com.br/lojaie/portal/pages/pdf/apostila_pqo_cap_01_v2.pdf
INTRODUÇÃO
O tema que iremos estudar recebe diversos nomes, em cada livro que é
tratado.
No livro de Laureano e Leite (1987), o tema recebe o nome de Financiamento
(Sistema Price). Entendo que o Sistema Price é importante, porém, ele deve ser
estudando junto com os Sistemas de Amortização de empréstimos ou financiamentos,
evitando maiores confusões.
No livro de Marcondes (1982), o nome utilizado é Financiamento, porém, no
mesmo capítulo trata-se de Aplicações.
Em Spinelli e Souza (1998) usa-se o termo Capitalização e Amortização. Como
trata-se do livro mais utilizado em escolas técnicas, o termo acabou se popularizando,
porém, achamos inadequado, pois, capitalização refere-se a qualquer tipo de juros, e
amortização pode levar ao entendimento de estarmos trabalhando os Planos de
Amortização.
Teixeira e Pierro Netto (1998) usa o nome Série Uniforme de Prestações
Periódicas, porém, fala no mesmo capítulo de “Parcelas Intermediárias”. O título não é
de todo inadequado, porém, preferimos não utilizá-lo.
Faria (1974) chama o assunto de rendas constantes na capitalização
composta, o que é adequado, porém, esquece que tratamos aqui também de
financiamentos.
O nome “financiamento” é polêmico, pois, no cotidiano, financiar significa pedir
empréstimo para coisa certa.
Para o dicionário Aurélio, versão online, “financiar” é verbo transitivo que
significa: “fornecer dinheiro, fundos, capitais; custear as despesas, a compra de
alguma coisa.”
O dicionário Houaiss é mais incisivo com a palavra “financiar” como “abonar
dinheiro para algum empreendimento; custear”.
A rigor a palavra mais adequada para Financiamento seria Empréstimo. Porém,
vamos preferir a palavra Financiamento.
Usaremos a seguinte terminologia
 Financiamento – receber algum dinheiro ou coisa de certo valor, a ser pago
no futuro, em prestações. São exemplos de financiamentos em nosso conceito:
o Empréstimos;
o Leasing;
o Crediários;
o CDC – Crédito Direto ao Consumidor;
o Financiamentos propriamente ditos.

23
 Aplicação – investimento de alguma quantia em agência bancária, instituição
financeira, bolsa de valores ou similar, para no futuro receber recursos. Aqui
estão incluídos:
o Todo tipo de investimento e aplicação no sistema bancário, inclusive
Cadernetas de Poupança;
o Compra de ações;
o Empréstimos para outras pessoas (factoring ou agiotagem);
o Venda de bens.
Para entendermos o que vamos estudar, vamos considerar nessa parte do
estudo, as seguintes condições:
 Os pagamentos ou recebimentos serão feitos em determinados prazos.
 As entradas ou saídas terão vencimentos periódicos.
 A primeira prestação ou aplicação pode incidir no começo do período, ou seja,
no ato da compra ou após.
Utilizaremos a seguinte terminologia:
 Termos ou Rendas ou Parcelas ou Prestações Antecipadas – quando é
pago certo valor no ato da compra.
 Termos ou Rendas ou Parcelas ou Prestações Imediatas ou Postecipadas
– quando a primeira prestação é paga exatamente um período após a compra.
Ex: se a taxa de capitalização é mensal, paga-se 1 mês depois da compra.
 Termos ou Rendas ou Parcelas ou Prestações Diferidas ou com carência
– quando é estabelecido o pagamento em tempo diferente do ato da compra ou
de 1 mês depois da compra. Nesse caso os cálculos são mais complexos, e
não estudaremos aqui.
Para compreendermos, vamos começar estudando os casos com Fluxo de
Caixa Homogêneo, ou seja, todos os pagamentos em igual valor, em determinados
prazos.
Vamos usar as seguintes siglas
VP = valor presente, em alguns casos Capital Inicial C ou Principal P
VF = valor futuro, em alguns casos Montante M
PMT = valor das prestações ou aplicações
FINANCIAMENTOS
Caso 1 – Com pagamentos imediatos
Nesse caso, a primeira prestação (ou aplicação) é paga (ou recebida) em um
período após a contratação. Como as prestações são iguais ao longo do período,
dizemos que o fluxo de caixa é homogêneo com termos imediatos ou postecipados.
Tratando-se de um compra a prazo ou do pagamento de um empréstimo ou
financiamento, chamaremos de FINANCIAMENTO, podemos pensar no seguinte fluxo
de caixa:
Ora, o Valor Presente, do 1º caso, pode ser calculado pelo seguinte somatório

24
𝑉𝑃 =
𝑃𝑀𝑇
1 + 𝑖
+
𝑃𝑀𝑇
(1 + 𝑖)2
+
𝑃𝑀𝑇
(1 + 𝑖)3
+ ⋯ +
𝑃𝑀𝑇
(1 + 𝑖) 𝑛
Utilizando-se a fórmula da soma dos termos de uma P.G. temos que:
𝑉𝑃 = 𝑃𝑀𝑇 × [
(1+𝑖) 𝑛−1
(1+𝑖) 𝑛×𝑖
] ou ainda que 𝑃𝑀𝑇 = 𝑉𝑃 × [
(1+𝑖) 𝑛×𝑖
(1+𝑖) 𝑛−1
]
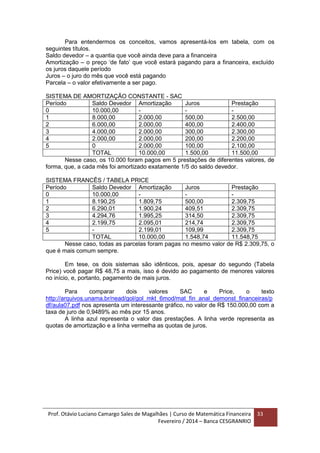
Quando estamos falando de cálculo de parcelas do pagamento de
empréstimos, financiamentos, compras, etc, chamamos de amortização. A expressão
(1+𝑖) 𝑛−1
(1+𝑖) 𝑛×𝑖
é chamada de fator de correção da amortização, e é internacionalmente
representada por 𝑎 𝑛ℸ𝑖 havendo inclusive tabelas desse valor. A expressão 𝑎 𝑛ℸ𝑖 Lê-se
“a n-cantoneira i”.
Dessa forma, o cálculo do VP=𝑎 𝑛ℸ𝑖xPMT .
Caso 2 – Com pagamentos antecipados
Caracteriza-se quando a primeira prestação (ou aplicação) é paga (ou recebida) no ato
da contratação. Lembre-se que estamos falando de fluxo de caixa homogêneo, nesse
caso, a “entrada” é igual a todas outras prestações/aplicações.
Veja os fluxos de caixa, respectivamente, para algo a ser pago em parcelas ou
para uma aplicação feita em um banco ou similar:
Usando a mesma lógica anterior, temos para o 1º caso:
𝑉𝑃 = 𝑃𝑀𝑇 × [
(1+𝑖) 𝑛−1
(1+𝑖) 𝑛×𝑖
] × (1 + 𝑖) e também 𝑃𝑀𝑇 = 𝑉𝑃 × [
(1+𝑖) 𝑛×𝑖
(1+𝑖) 𝑛−1
] ×
1
1+𝑖
APLICAÇÕES
Caso 1 – Com aplicações imediatas
Tratando-se de um investimento ou aplicação, chamaremos simplesmente de
APLICAÇÃO a ser feita para gerar lucros, podemos pensar no seguinte fluxo de caixa:
Para o cálculo do Valor Futuro, do 2º caso, basta fazer a somatória das
aplicações corrigidas pela taxa de juros vigente. Ou seja:
VF=PMTx(1+i)+PMTx(1+i)2
+PMTx(1+i)3
+...+PMTx(1+i)n
Realizando as simplificações com a fórmula da P.G. temos que:
𝑉𝐹 = 𝑃𝑀𝑇 × [
(1+𝑖) 𝑛−1
𝑖
] ou ainda 𝑃𝑀𝑇 = 𝑉𝐹 × [
𝐼
(1+𝑖) 𝑛−𝑖
]

25
O símbolo 𝑆 𝑛ℸ𝑖 , lê-se “S n-cantoneira i”, é utilizado para representar
(1+𝑖) 𝑛−1
𝑖
de tal
forma que podemos escrever que VF=PMT. 𝑆 𝑛ℸ𝑖, muito utilizado em livros de
Matemática Financeira. Há inclusive tabelas do 𝑆 𝑛ℸ𝑖.
Caso 2 – Com aplicações antecipadas
E para o 2º caso:
𝑉𝐹 = 𝑃𝑀𝑇 × [
(1+𝑖) 𝑛−1
𝑖
] × (1 + 𝑖) ou ainda 𝑃𝑀𝑇 = 𝑉𝐹 × [
𝐼
(1+𝑖) 𝑛−𝑖
] ×
1
1+𝑖
Para calcular 𝑆 𝑛ℸ𝑖 e 𝑎 𝑛ℸ𝑖 na calculadora HP 12C basta fazer os cálculos normais
utilizando a taxa n, o tempo i, e PV(para 𝑎 𝑛ℸ𝑖 ) ou FV (para 𝑆 𝑛ℸ𝑖 ) com o número 1.
SIMBOLOS UTILIZADOS
São as mesmas fórmulas, acrescidas de (1+i), ou de seu inverso, conforme o
caso.
Símbolos nos variados livros
SPINELLI, SOUZA (1998)
FARIA (1974)
LAUREANO, LEITE (1987)
MORAES, PRIMO (1998)
CARVALHO (1968)
MARCONDES (1995)
TEIXEIRA, PIERRO
NETTO (1998)
(1+i)n
- FPS F.A.C.
1
(1 + i)n
- FSP F.V.P.
(1 + 𝑖) 𝑛
− 1
(1 + 𝑖) 𝑛 × 𝑖 𝑎 𝑛ℸ𝑖
FRP
F.V.P.m
(Fator Valor Presente por
Operação Múltipla)
(1 + 𝑖) 𝑛
× 𝑖
(1 + 𝑖) 𝑛 − 1
1
𝑎 𝑛ℸ𝑖
FPR -
(1 + 𝑖) 𝑛
− 1
𝑖 𝑠 𝑛ℸ𝑖
FRS
F.A.C.m
(Fator de Acumulação de
Capital por Operação
Múltipla)
𝐼
(1 + 𝑖) 𝑛 − 𝑖
1
𝑠 𝑛ℸ𝑖
FSR -

26
MÉTODOS DE VERIFICAÇÃO DE RISCO
Método 1 - Valor Presente Líquido
O Valor Presente Líquido – VPL – é um método de análise e avaliação de
projetos de investimentos. Seu objetivo é determinar o valor do projeto no instante
zero do fluxo de caixa, dados taxa de juro e o tempo (inclusive tempo contínuo), as
despesas e receitas futuras.
Nesse caso, a taxa de juro considerada é uma taxa mínima de retorno
esperada. Trata-se apenas de um método para avaliar a aplicação.
O investimento será viável se a taxa de retorno obtida no projeto for igual ou
maior à taxa de retorno dessas aplicações, ou seja, o retorno esperado pelo
investimento deverá ser maior do que seu custo de oportunidade (o retorno obtido nas
outras aplicações livres de risco).
Para calcular o VPL utiliza-se a seguinte fórmula:
𝑉𝑃𝐿 = −𝑉𝑃 +
𝑉𝐹1
(1 + 𝑖)1
+
𝑉𝐹2
(1 + 𝑖)2
+
𝑉𝐹3
(1 + 𝑖)3
+ ⋯ +
𝑉𝐹𝑛
(1 + 𝑖) 𝑛
VPL = valor presente líquido
VP = valor presente do fluxo de caixa
VFt = valor futuro do fluxo de caixa, negativo (saída) ou positivo (entrada)
i = taxa de juro mínima do investimento.
Teremos então
VPL<0 – nesse caso a taxa de retorno do investimento é menor que a mínima
desejada. A realização do projeto não é recomendável.
VPL>0 – nesse caso a taxa de retorno do investimento é maior que a mínima
desejada. Ou seja, a realização do projeto é recomendável.
VPL=0 – nesse caso a taxa de retorno é igual a mínima desejada. É indiferente
realizar ou não o projeto.
Quanto maior o VPL, maior será o retorno investimento.
Método 2 - Taxa Interna de Retorno
É outro método de análise de projetos de investimento e aplicações financeiras.
Nesse caso equaliza-se o valor presente de um ou mais pagamentos com o valor
presente de um ou mais recebimentos. Ou seja, é o cálculo da taxa que zera o VPL.
−𝑉𝑃 +
𝑉𝐹1
(1 + 𝑖)1
+
𝑉𝐹2
(1 + 𝑖)2
+
𝑉𝐹3
(1 + 𝑖)3
+ ⋯ +
𝑉𝐹𝑛
(1 + 𝑖) 𝑛
Figura adaptada de:
http://lojavirtual.bmf.com.br/lojaie/portal/pages/pdf/apostila_pqo_cap_01_v2.pdf
Caso se encontre duas ou mais raízes, o que é possível (no caso taxas
internas de retorno múltiplas), recomenda-se a utilização do método VPL.

27
O projeto é viável quando a TIR for maior que a taxa mínima considerada para
o projeto.
O VPL também é chamado de NPV (Net Present Value) e a Taxa Interna de
Retorno de IRR (Internal Rate of Return), com teclas próprias na HP 12C.
Vamos supor que o fluxo de caixa com taxa 2% mostre
Estando f REG pressionandos, para calcular VPL e TIR basta:
50 g CFj
30 g CFj
25 g CFj
12 g CFj
30 g CFj
2 i
f NPV – vai mostrar a VPL
f IRR – vai mostrar a TIR
Obs: caso haja várias parcelas iguais, por exemplo, com taxa de 2%:
30 g CFj
3 g Nj (dizendo que o fluxo repete-se por 3 vezes)
20 g CFj
2 g Nj
8 g CFj
15 g CFj
2 g Nj
f NPV
g IRR
EXERCÍCIOS
1. Um empresário aplica R$ 500,00 durante dois meses num fundo especial que
rendia 10% ao mês. Porém, ele desistiu do fundo e resolveu resgatar o valor.
Considerando termos postecipados, qual será o valor do resgate?
2. Um eletrodoméstico foi comprado na loja “Arrancacouro” para começar a ser pago
daqui a 30 dias, em 16 parcelas iguais de R$ 800 com taxa de juro de 3%. Qual é o
valor atual do eletroméstico? Dado (1,03)16
=1,6.
3. O Sr Munheca deseja fazer uma aplicação de renda fixa a uma taxa de 2% ao mês
para resgatar R$ 10.000,00. Em quantos anos aproximadamente o Sr. Munheca irá
resgatar esse valor se aplicar R$ 100,00 por mês? Dado log(102)=2,0086 e
log(103)=2,012837.
4. Quanto terei no final de 10 meses se aplicar, a partir de hoje, R$ 1200,00
mensalmente no Banco Tápraquebrá que paga uma taxa de juros compostos de 20%
ao mês? Dado (1,2)10
=6,2.

28
5. A Loja EletroBucanas vende uma geladeira em uma entrada e mais 10 parcelas
mensais de R$ 40,00 com taxa de juros de 5% ao mês. Qual seria o valor da compra
dessa geladeira à vista? Dado
1,0511−1
1,0511.0,05
= 8,3.
6.Utilizando a tabela resolva os seguintes exercícios.
a) Um carro está sendo vendido em 12 prestações de R$ 800,00, sendo o primeiro
pagamento efetuado daqui a 30 dias e a taxa de juros de 5%. Qual é o valor desse
carro?
b) Um fogão custa R$ 500,00 e será vendido em 8 prestações mensais, sem entrada,
com taxa de juros mensais de 4%. Qual será o valor das prestações?
c) Um fogão custa R$ 524,21. Qual será o valor mensal das prestações, sendo a
primeira daqui a 30 dias, com 4% de juros, e pagamento durante 6 meses?
d) Uma geladeira será vendida com uma entrada e mais 8 parcelas, todas no valor de
R$ 100,00. Sendo a taxa de juros de 3%, quanto custa a geladeira?
e) Um carro foi avaliado em R$ 7.722,00. Considerando que ele será pago em
parcelas mensais de R$ 1000,00 sem entrada a uma taxa de 5%, determine em
quantos meses o carro será totalmente pago.
f) Um aparelho no valor de R$ 1.000,00 está sendo vendido em parcelas de R$ 117,20
sem entrada. Quantas serão as parcelas necessárias para quitar a dívida se a taxa de
juros é de 3%?
g) Uma casa foi avaliada em R$ 99.540,00. O Sr. Patinhas pretende pagá-la em
poucas parcelas, dispondo a pagar parcelas mensais de R$ 10.000,00 sem entrada, a
uma taxa de juros de 4%. Em quantos meses terminará de pagar a casa?

29

30
QUESTÕES – Use as tabelas – calculadora apenas para verificação e cálculos de
divisão e multiplicação
1) Qual será o montante de uma aplicação de R$ 8.000,00 a uma taxa mensal de 8%,
em termos imediatos, durante 12 meses?
2) Qual será o valor da prestação mensal aplicada por 1 ano sem entrada, com taxa
de juros de 26,82% capitalizado mensalmente, para gerar um total de R$ 134.120,99?
3) O Banco “DaPraça” anuncia que um depósito de R$ 100,00 mensal, aplicado por 2
anos em termos postecipados, gerará um valor de resgate de R$ 3.442,65. Qual é a
taxa mensal de juro composto do investimento?
4) Quantos anos eu preciso aplicar anualmente R$ 2.000,00, em termos postecipados,
para ter R$ 20.213,00 reais a taxa de 15% de juros anuais?
5) Calcule o valor de resgate de um investimento feito em 12 parcelas de R$
10.000,00 colocadas mensalmente a juros de 3%, sendo a primeira parcela
antecipada.
6) Pretendo comprar um computador no valor de R$ 1.000,00 e para isso faço um
investimento de renda fixa a taxa de juros de 8%, aplicando R$ 100,00 todos os
meses. Em quanto tempo terei o dinheiro que preciso?
7) O Sr. MotoTonto foi comprar na concessionária “Lata Velha” uma moto que lhe foi
vendido em 10 prestações mensais sem entrada com taxa de 5% a.m e prestações de
R$ 100,00. Qual é o valor da moto?
8) O Dr. RicoÀBeça quer comprar uma casa que custa R$ 101.058,95. Sabendo que
ele pode pagar mensalmente prestações de R$ 10.000,00. Sendo a taxa de juros
mensais de 6%, e a primeira prestação a ser paga daqui a 30 dias, quantas serão as
parcelas pagas?
9) Uma cadeira de rodas será vendida em 10 prestações com uma taxa de juros
simbólico apenas 1% ao mês. Sabendo que o preço dessa cadeira de rodas é de R$
1.895,00, qual será o valor mensal das parcelas?
10) Pagando 13 prestações mensais de R$ 400,00 num financiamento feito à base de
8% a.m., que dívida estarei amortizando?
11) Comprei um ônibus para levar alunos para fazer a prova do Banco do Brasil em
Passos. O preço à vista era de R$ 12.000,00. Pagando-o em 12 prestações mensais,
sem entrada, de R$ 1.205,54, qual foi a taxa mensal de juro cobrada?
12) Quantos meses gastarei para pagar uma dívida de R$ 12.000,00 pagando em
parcelas mensais de R$ 800,00, com a primeira parcela daqui a um mês, num
financiamento com taxa de juros mensal de 5%?
13) Qual a opção mais vantajosa para um financiamento de R$ 11.000,00 (adaptado
de SPINELLI e SOUZA)
a) 12 prestações de R$ 1.384,92 ou
b) 18 prestações de R$ 1.015,92?
14) Um carro é vendido em 6 prestações mensais, sem entrada, de R$ 2.142,31 ou
em 12 prestações mensais de R$ 1.087,43, sendo a taxa de juros de 2%. Qual das
duas aplicações é mais vantajosa?
15) Uma máquina fotográfica foi vendida em 4 prestações de R$ 100,00 com taxa de
juros de 36% com capitalização mensal. Se ela fosse vendida à vista teria um
desconto de 20% sobre o preço de tabela. Qual seria o desconto caso ela fosse
vendida à vista?
16) Calcule a parcela antecipada de um financiamento de R$ 5000,00 feito em 12
parcelas mensais iguais a 2% de juro.

31
EXERCÍCIOS – DO MATERIAL DA BM&F
1) A loja Promocional está anunciando a venda de televisores de 20 polegadas a R$
600,00 a vista ou em 10 parcelas iguais e mensais, sendo o primeiro pagamento feito
30 dias depois da compra. A taxa de juros praticada pela loja é de 1,5% ao mês. Com
base nestas informações, calcule o valor das prestações.
Resposta: R$ 65,06
2) O “Sr. Endividado” obteve um financiamento, na modalidade Crédito Direto ao
Consumidor (CDC). Restam 20 parcelas mensais para serem amortizadas, inclusive a
que vence no final deste mês, no valor de R$ 1.759,03. A taxa de juro praticada pela
instituição financeira é de 3,5% ao mês. Com tais dados, calcule o valor presente do
financiamento.
Resposta: R$ 25.000,04
3) A concessionária Bom Passeio está vendendo um carro “X” a R$ 30.000,00 a vista
ou em 36 parcelas mensais de R$ 1.175,10, sendo o primeiro pagamento feito em 30
dias. Calcule a taxa de juros mensal praticada pela empresa.
Resposta: 1,99% a.m.
4) Certo cliente necessita fazer um financiamento no valor de R$ 7.000,00 para a
compra de um veículo, porém pode apenas dispor de R$ 555,00 mensais para
pagamento. Sabendo que a taxa de juros da instituição financeira que realizará o
financiamento é de 2,25% ao mês e que o pagamento é postecipado, calcule o
período de tempo da amortização da dívida.
Resposta: 15 meses
5) Sabendo que a caderneta de poupança tem rendimento médio de 0,9% ao mês, um
investidor gostaria de saber quanto deve aplicar mensalmente para obter, após 12
meses, a quantia de R$ 10.000,00. Considere que a primeira aplicação será feita
daqui a 30 dias.
Resposta: R$ 792,88.
3) O “Sr. Econômico” aplica todo mês uma quantia de R$ 2.000,00 em um fundo que
vem rendendo 1,5% ao mês. Considerando que esta aplicação seja efetuada durante
18 meses, calcule o valor futuro (ou valor de resgate) deste investimento. Utilize o
conceito de termos postecipados.
Resposta: R$ 40.978,75.
7) Uma pessoa física obteve um financiamento na modalidade CDC (Crédito Direto ao
Consumidor) no valor de R$ 50.000,00 para ser amortizado em 120 parcelas mensais
iguais e consecutivas. Sabendo que a taxa de juros praticada é de 16% ao ano e que
os pagamentos são antecipados, calcule o valor das aplicações.
8) Calcule o valor presente do financiamento feito por um consumidor para a compra
de uma geladeira, sabendo que o pagamento deve ser efetuado da seguinte forma:
entrada de R$ 185,00 mais 11 prestações de R$ 185,00, com taxa de juro de 2,85%
ao mês.
9) Calcule a taxa de juro mensal de um financiamento no valor de R$ 35.000,00 para a
compra de um veículo, sendo que a amortização ocorrerá em 24 parcelas, mensais e
consecutivas de R$ 1.636,60, com a primeira delas vencendo no ato da contratação.
Resposta: 1,03% ao mês.
10) Um lojista toma um financiamento no valor de R$ 10.000,00 para realizar alguns
reparos em seu estabelecimento. Tendo consciência de que apenas pode honrar
parcelas de, no máximo, R$ 400,00 mensais e sabendo que a taxa de juro do banco
com o qual trabalha é de 1,99% ao mês, calcule o período de tempo necessário para
quitar a dívida. Considere que o pagamento seja com termos antecipados.
Resposta: 34 meses

32
11) Calcule a quantia que devo aplicar hoje (valor da aplicação) em títulos privados
com taxa de juros compostos de 1,60% ao mês para obter um valor futuro (ou de
resgate), daqui a 24 meses, de R$ 30.000,00. Considere que os termos sejam
antecipados.
12) Certo cliente do Banco XLS deseja saber o valor futuro a ser resgatado daqui a 12
meses, caso aplique mensalmente 10% de seu salário de R$ 3.950,00 em um fundo
de renda fixa com taxa de juro de 1,3% ao mês.
13) O Sr. Build está analisando a possibilidade de realizar um investimento que
provavelmente lhe proporcionará receitas anuais de R$ 25.000,00 durante três anos.
O fluxo abaixo mostra que, ao realizar um investimento inicial de R$ 45.000,00,
projetam-se retornos futuros anuais não variáveis. Qual o valor presente líquido do
fluxo de caixa apresentado abaixo, considerando uma taxa de juros anual de 14%? O
investimento deverá ou não ser realizado?
Resposta: R$ 13.040,80. Sim.
14) O Sr. José solicitou um empréstimo de R$ 90.000,00 que será pago em três
prestações mensais consecutivas de R$ 45.000,00. Determine a taxa interna de
retorno dessa operação sob a ótica do credor.
Resposta: 23,37%.
Empréstimos e Sistemas de Amortização
SAC E TABELA PRICE
Os empréstimos por parte das financeiras são feitos com longos prazos, em
geral dilatados. As parcelas são pagas através de diversas maneiras. Ou pagando
parcelas todas iguais, ou pagando parcelas cada vez menores.
Há dois sistemas mais comuns de amortização dos empréstimos, entre vários:
- Sistema de Amortização Constante (SAC) ou Sistema Hamburguês
- Sistema de Amortização Francês ou Tabela Price
PROBLEMA GERADOR
Quais serão as parcelas a serem pagas de um financiamento de R$ 10.000,00,
em 5 meses, à taxa de 5% a.m.?
Vamos fazer as seguintes tabelas para entendimento.

33
Para entendermos os conceitos, vamos apresentá-los em tabela, com os
seguintes títulos.
Saldo devedor – a quantia que você ainda deve para a financeira
Amortização – o preço ‘de fato’ que você estará pagando para a financeira, excluído
os juros daquele período
Juros – o juro do mês que você está pagando
Parcela – o valor efetivamente a ser pago.
SISTEMA DE AMORTIZAÇÃO CONSTANTE - SAC
Período Saldo Devedor Amortização Juros Prestação
0 10.000,00 - - -
1 8.000,00 2.000,00 500,00 2.500,00
2 6.000,00 2.000,00 400,00 2.400,00
3 4.000,00 2.000,00 300,00 2.300,00
4 2.000,00 2.000,00 200,00 2.200,00
5 0 2.000,00 100,00 2.100,00
TOTAL 10.000,00 1.500,00 11.500,00
Nesse caso, os 10.000 foram pagos em 5 prestações de diferentes valores, de
forma, que, a cada mês foi amortizado exatamente 1/5 do saldo devedor.
SISTEMA FRANCÊS / TABELA PRICE
0 10.000,00 - - -
1 8.190,25 1.809,75 500,00 2.309,75
2 6.290,01 1.900,24 409,51 2.309,75
3 4.294,76 1.995,25 314,50 2.309,75
4 2.199,75 2.095,01 214,74 2.309,75
5 - 2.199,01 109,99 2.309,75
TOTAL 10.000,00 1.548,74 11.548,75
Nesse caso, todas as parcelas foram pagas no mesmo valor de R$ 2.309,75, o
que é mais comum sempre.
Em tese, os dois sistemas são idênticos, pois, apesar do segundo (Tabela
Price) você pagar R$ 48,75 a mais, isso é devido ao pagamento de menores valores
no início, e, portanto, pagamento de mais juros.
Para comparar dois valores SAC e Price, o texto
http://arquivos.unama.br/nead/gol/gol_mkt_6mod/mat_fin_anal_demonst_financeiras/p
df/aula07.pdf nos apresenta um interessante gráfico, no valor de R$ 150.000,00 com a
taxa de juro de 0,9489% ao mês por 15 anos.
A linha azul representa o valor das prestações. A linha verde representa as
quotas de amortização e a linha vermelha as quotas de juros.

34
Todos os sistemas podem ser feitos com prazos de carência, e, para eles,
basta seguir a mesma lógica que já fizemos anteriormente em todo o curso. Vamos
nos focar nesses dois sistemas e nos cálculos.
Fórmulas que podem ser aplicadas.
Análogo ao que já estudamos, dá para concluir facilmente que as parcelas fixas
do sistema Price são calculadas por VP=𝑎 𝑎𝑎𝑎xPMT . O que é evidente, pelo que já
estudamos.
EXERCÍCIOS
1) Um banco financia R$ 5.000,00 a um cliente, com base na tabela Price e a juros de
15% a.a., para serem devolvidos em 10 meses. Construa o plano de amortização
dessa dívida.
0
1
2
3
4
5
6
7
8
9
10

35
2) Um empréstimo de R$ 15.000,00 pelo Sistema Francês de Amortização deve ser
pago em 1 ano, sem carência, à base de 4% a.m. de juros. Construa o plano de
amortização para esse caso.
0
1
2
3
4
5
6
7
8
9
10
11
12
3) Um carro no valor de R$ 40.000,00 é comprado, sem entrada, para ser pago em 8
meses, com carência de 2 meses, à base de 9% a.m. de juros, capitalizado inclusive
durante a carência. Sabendo que o financiamento feito pelo SAC, monte o plano de
amortização.
0
1
2
3
4
5
6
7
8
9
10
4) Um empréstimo de R$ 30.000,00 deve ser pago em 4 parcelas trimestrais iguais,
com juros de 10% em cada trimestre. Construa o plano de amortização.
0
1
2
3
4

36
5) Um financiamento de R$ 50.000,00 é feito, sem prazo de carência, à taxa de 20%
a.a. (tabela Price), devendo ser devolvido em 5 prestações mensais. Monte o plano de
financiamento.
0
1
2
3
4
5
6) Faça o mesmo exercício 5 pelo SAC.
0
1
2
3
4
5
7) O Sistema de Amortização Misto (SAM) é igual a média entre o Sistema Price e o
SAC. Com orientações do professor, construa o plano SAM com os mesmos dados do
exercício 5.
0
1
2
3
4
5
OUTROS TEMAS EM MATEMÁTICA FINANCEIRA
FLUXO DE CAIXA HETEROGÊNEO
Ocorre quando as parcelas são diferenciadas, podendo ser postecipado (imediato) ou
antecipado.
EXERCÍCIO

37
1) O Sr. Calculista está analisando um determinado projeto de investimento do qual
deseja uma rentabilidade mínima de 2,5% ao mês. O quadro a seguir mostra que ao
realizar um investimento inicial de R$ 28.000,00, projetam-se retornos futuros mensais
variáveis. Calcule o VPL do fluxo de caixa e avalie se o investimento deve ser feito ou
não.
Resposta: - R$ 1.499,06. Não deve ser feito.
2) Uma empresa deseja realizar alguns reformas em seu prédio. Para tanto, quer
saber quanto deve depositar em conta para fazer as retiradas apresentadas no quadro
abaixo, sabendo que a remuneração dos depósitos é de 1,5% ao mês.
Resposta: VPL=R$ 22.871,47
3) O Sr. Investidor deseja saber o PU (preço unitário) de uma debênture, cujo valor
nominal é R$ 1.000,00, sendo que a taxa de juros compostos que remunera a
aplicação é de 10% ao ano, o pagamento dos juros é semestral e o resgate ocorrerá
em 10 semestres. Este agente considera uma taxa de juro mínima de 15% ao ano
para o seu investimento.
4) O Sr. “No Vermelho” solicitou um empréstimo de R$ 80.000,00 que será pago em
três prestações mensais consecutivas de R$ 40.000,00, R$ 35.000,00 e R$ 15.000,00.
Determine a taxa interna de retorno (TIR) desta operação sob a ótica do banco.
Resposta: 7,16%
RENDAS DIFERIDAS (FINANCIAMENTO COM CARÊNCIA)
Para calcular basta utilizar a fórmula que é facilmente deduzível
𝑎𝑎 = 𝑎𝑎𝑎(𝑎 𝑎𝑎𝑎 − 𝑎 𝑎𝑎𝑎
Sendo k = período de carência, m=k+n.
EXERCÍCIOS
1) Uma grande loja anuncia “Compre tudo e pague em 10 vezes. Leve hoje e só
comece a pagar daqui a 3 meses”. Se a taxa de financiamento é de 3,8% a.m., qual
será o valor da prestação de uma geladeira cujo preço à vista é de R$ 2.800,00.
2) Uma amortização constante de 20 parcelas mensais de R$ 860,00 tem carência de
6 meses e taxa mensal de 2%. Qual é o valor do financiamento na ocasião do
contrato?
Resposta: R$ 12.487,11.
3) Calcular o valor atual de uma renda mensal de 12 termos iguais a R$ 2.000,00 com
carência de 4 meses, sendo a taxa de juros de 5% a.m.
TAXA OVER
Chamada de taxa nominal over uma taxa de aplicações financeiras de prazo
curto, como cheques especiais, fundo de investimentos, o not money e outras.
Ela considera apenas a quantidade de dias úteis que os juros serão
capitalizados.
𝑎 𝑎𝑎𝑎𝑎𝑎𝑎𝑎 = (1 +
𝑎 𝑎𝑎𝑎𝑎
30
)
𝑎
− 1
Sendo i a taxa efetiva ou over, u o número de dias úteis.

38
É a mesma lógica das taxas equivalentes.
EXERCÍCIO
1) Calcule a taxa over equivalente a uma taxa efetiva de 10% a.m, para uma aplicação
feita numa segunda-feira com duração até na quinta-feira da semana seguinte.
TAXA REAL CONSIDERANDO A INFLAÇÃO
Cuidado para não confundir com o uso do nome “taxa efetiva ou real”. Aqui
quer saber a taxa verdadeira.
(1+it)=(1+ir)(1+ii)
Sendo it a taxa total, ir a taxa ‘de fato’ e ii a taxa de inflação.
EXERCÍCIO
1) Se entre duas épocas ocorre uma inflação de 7%, qual deve ser a taxa real de juro
para se obter uma taxa total de um investimento de 10%?
TABELAS DE MATEMÁTICA FINANCEIRA
𝑎 𝑎𝑎𝑎
No Excel VF(taxa;período;1;;0)

39
𝑎 𝑎𝑎𝑎
No Excel VP(taxa;período;1;;0)
REFERÊNCIAS BIBLIOGRÁFICAS
ASSAF NETO, Alexandre; LIMA, Fabiano Guasti. Investimento no Mercado
Financeiro Usando a Calculadora Financeira HP 12C. Ribeirão Preto: Inside Books,
2008.
CARVALHO, Thales Mello. Matemática Para os Colégios Comerciais. Rio de
Janeiro: MEC, 1968.
FARIA, Rogério Gomes de. Matemática Comercial e Financeira. São Paulo:
McGraw-Hill do Brasil, 1974.
LAUREANO, José Luiz; LEITE, Olímpio Vissoto. Os Segredos da Matemática
Financeira. São Paulo, Ed. Ática, 1986.
MARCONDES, Oswaldo. Matemática Financeira. São Paulo: Ed. Ática, 1982.
MORAES, José Forêncio de; PRIMO, Ângelo. Matemática. In: Concurso Público
para Escriturário do Banco do Brasil. São Paulo: Apostilas Solução, 1998.
SPINELLI, Walter; SOUZA, M. Helena S. Matemática Comercial e Financeira. São
Paulo: Ed. Ática, 1998.
TEIXEIRA, James; PIERRO NETO, Scipione. Matemática Financeira. São Paulo:
Makron Books, 1998.
TOSSI, Armando José. Matemática Financeira Com Utilização da HP-12C. São
Paulo: Atlas, 2006.

40
Questões da CESGRANRIO
PROVA DO BANCO DO BRASIL – ESCRITURÁRIO – CESGRANRIO – 2012

41

42

43
PROVA DO BANCO DO BRASIL – ESCRITURÁRIO – CESGRANRIO – 2010

44

45
QUESTÕES DA CESGRANRIO – 2011 A 2013 – RENDAS CERTAS,
FINANCEIRAS OU ANUIDADES
Site http://rotadosconcursos.com.br/questoes-de-concursos
1) (Técnico de Suprimento Jr. – Petrobrás – CESGRANRIO – 2013) Um bem cujo
preço à vista é R$ 10.100,00, é vendido em doze prestações consecutivas, mensais e
iguais, sendo a primeira prestação no ato da compra.
Se são cobrados juros compostos de 1% ao mês, o valor das prestações, em reais, é
aproximadamente.
Dado (1,01)-12
=0,8874
a) 842 b) 888 c) 897 d) 914 e) 948
2) (Arquiteto (Superior) – Caixa Econômica Federal – CESGRANRIO – 2012) Um
bem, cujo preço à vista é R$ 30.000,00, é vendido com uma entrada de 10%, e o
restante, em 72 prestações mensais iguais, sendo a primeira paga um mês após a
compra.
Se os juros são de 12% ao ano, capitalizados mensalmente, o valor das prestações é,
em reais, aproximadamente, de
a) 420 b) 529 c) 588 d) 2.471,00 e) 3.240,00

46
3) (Técnico em Suprimento de Bens Jr. – Administração – Petrobrás –
CESGRANRIO – 2011) Utilize a tabela, se necessário, para resolver a questão.
Um capital é aplicado à taxa composta de 3% ao bimestre durante 10 meses. Ao final
do prazo, os juros gerados são reaplicados por 1 ano à taxa nominal de 12% ao ano
com capitalização trimestral, resultando em um montante de R$ 2.420,18. O valor, em
reais, mais próximo do capital aplicado é
a) 13.592 b) 13.497 c) 13.328 d) 13.207 e) 13.152
4) (Técnico em Suprimento de Bens Júnior – Administração – Petrobrás – 2013)
Aplicaram-se R$ 10.000,00 por nove meses à taxa nominal de 12% ao ano com
capitalização trimestral. No momento do resgate, pagou-se Imposto de Renda de
alíquota 15%, sobre os rendimentos. O valor líquido do resgate foi, em reais, mais
próximo de
a) 10.927 b) 10.818 c) 10.787 d) 10.566 e) 9.287
5) (Contador Jr. – Contábil – Petrobrás Transporte – CESGRANRIO – 2011) Um
título de renda fixa deverá ser resgatado por R$ 15.000,00 no seu vencimento, que
ocorrerá dentro de 2 meses. Sabendo-se que o rendimento desse título é de 1,5% ao
mês (juros compostos), o seu valor presente, em reais, é
a) 14.619,94 b) 14.559,93 c) 14.550,00 d) 14.451,55 e) 14.443,71
6) (Contador Jr. – Auditoria Interna – Petrobrás Transporte – CESGRANRIO –
2011) Uma loja de eletrodomésticos está realizando uma promoção em que na compra
de qualquer artigo até R$ 1.000,00, o pagamento será em uma única prestação 6
meses depois. Um consumidor adquiriu mercadorias no valor de R$ 800,00, sendo
informado de que a prestação a ser paga, dentro de 6 meses, seria de R$ 1.000,00. A
taxa mensal de juros composta cobrada pela loja está situada entre
a) 6% e 7% b) 5% e 6% c) 4% e 5% d) 3% e 4% e) 2% e 3%

47
2011) Um aplicador realizou um investimento cujo valor de resgate é de R$ 80.000,00.
Sabendo-se que a taxa de juros simples é de 3,5% ao mês e que faltam 5 meses para
o resgate, o valor da aplicação, em reais, foi de
a) 68.085,10 b) 66.000,00 c) 65.000,00 d) 64.555,12 e) 63.656,98
2011) Um aplicador realizou um investimento que deverá ter valor de resgate de R$
100.000,00 no seu vencimento, que ocorrerá dentro de 2 meses. Sabendo-se que a
taxa de juros compostos utilizada pelo banco é de 2% ao mês, o valor do investimento
original, em reais, foi de
a) 98.123,45 b) 96.116,88 c) 95.875,33 d) 94.781,29 e) 93.764,32
2011)Uma empresa obteve um desconto de uma duplicata no valor de R$ 12.000,00
no Banco Novidade S/A, com as seguintes condições:
• Prazo do título 2 meses
• Taxa de desconto simples cobrada pelo banco 2,5% ao mês
Considerando-se exclusivamente as informações acima, o valor creditado na conta
corrente da empresa, em reais, foi de
a) 11.660,00 b) 11.460,00 c) 11.400,00 d) 11.200,00 e) 11.145,00
2011)Um investidor aplicou, durante 3 anos, R$ 500,00 por mês em um Fundo de
Renda Fixa que oferece juros compostos de 1,5% ao mês. Ao final da aplicação,
obteve R$ 23.637,98. Esse tipo de operação, em matemática financeira, caracteriza o
modelo denominado
a) série de pagamentos iguais com termos antecipados
b) série de pagamentos iguais com termos vencidos
c) equivalência de capitais e de planos de pagamentos
d) aplicação equivalente de renda postecipada
e) aplicações financeiras com renda variável
11) (Administrador Jr. – Petrobrás Transporte – CESGRANRIO – 2011)
Um débito de R$ 350.000,00, contraído há 2 meses, está sendo amortizado com um
pagamento de R$ 45.000,00 hoje, R$ 130.000,00 de hoje a 3 meses e R$ 85.000,00
de hoje a 8 meses.
Que pagamento no fim de 5 meses, contados de hoje, em reais, ainda é necessário
ser feito para uma taxa de juros composta de 2% ao mês?
Dado: Considere, para os cálculos, os valores na tabela acima.
a) 137.156,90 b) 140.000,00 c) 158.000,30 d) 162.450,13 e) 173.460,35
12) (Administrador Jr. – Petrobrás Transporte – CESGRANRIO – 2011) Um cliente
obteve junto a um banco um empréstimo no valor de R$ 10.000,00 para pagamento
em 90 dias, a taxa de 8% ao mês, com capitalização mensal. Um imposto de 5%
incidente sobre o montante da operação (valor do principal e juros), é cobrado na data
de liberação do empréstimo. A partir dessas informações, qual o custo trimestral,
expresso em percentagem, a ser determinado para o cliente?
a) 13,00% b) 13,40% c) 34,44% d) 41,27% e) 44,19%

48
13) (Administrador Jr. – Petrobrás Transporte – CESGRANRIO – 2011) Uma
mineradora, em meio ao processo de planejamento financeiro, está analisando a
possibilidade de lançar debêntures não conversíveis no valor de R$ 20.000,00, com
valor nominal de R$ 1.000,00 cada debênture, prazo de 3 anos, e pagamento de juros
anuais ao final de cada ano, a uma taxa real de 10% ao ano.
Para efetivar o lançamento e tornar os papéis mais atrativos, a empresa pretende
vender as debêntures a um preço de R$ 980,00 por título, de forma a compensar a
taxa oferecida. Os responsáveis pela área financeira verificaram ainda a existência de
um custo de 2% sobre o valor nominal de cada título como remuneração para os
bancos interessados no lançamento.
Com base nas informações fornecidas e nos valores apresentados na tabela acima,
qual a faixa em que se encontra a taxa efetiva anual do lançamento das debêntures,
expresso em porcentagem?
14) (Administrador Júnior – Petrobrás Transporte – CESGRANRIO – 2011) Uma
empresa solicita um financiamento de R$ 2.000.000,00 pelo prazo de 360 dias,
pagando, a cada mês, os juros correspondentes e devolvendo integralmente o
principal no fim do prazo contratado. Sabendo-se que o credor cobra uma taxa de
juros de 3% ao mês, e o cliente, no ato da liberação do empréstimo, tem que pagar 1%
de imposto sobre o valor do empréstimo, o valor líquido recebido, o valor dos juros
mensais e o valor total pago além do principal, pelo cliente, são, em reais,
respectivamente,
a) 1.980.000,00 ; 60.000,00 ; 740.000,00
b) 1.970.000,00 ; 180.000,00 ; 210.000,00
c) 1.930.000,00 ; 85.000,00 ; 960.000,00
d) 1.920.000,00 ; 66.000,00 ; 668.000,00
e) 1.900.000,00 ; 720.000,00 ; 1.260.000,00
15) (Analista (Superior) – Análise de Garantias – FINEP – CESGRANRIO – 2011)
Uma loja de departamentos parcela a venda dos seus produtos em três prestações
mensais iguais, sendo a primeira paga no ato da compra. O regime é o de juros
compostos, e a taxa de juros é de 2% ao mês.
Para uma compra no valor de R$ 306,00, o valor da prestação mensal, em reais, é de,
aproximadamente,
a) 92,00 b) 104,00 c) 118,00 d) 153,00 e) 155,00
16) (Especialista em Regulação – Geral (Superior) – Agência Nacional do
Petróleo, Gás Natural e Biocombustível – CESGRANRIO – 2008) No início de
determinado mês, uma pessoa faz uma aplicação financeira de R$10.000,00, pelos
próximos seis meses. Recebe R$ 200,00 no início de cada um dos cinco meses
seguintes. No início do sexto mês, recebe um valor X e a aplicação se encerra. Se a
taxa de juros composta da aplicação for de 2% a.m., qual é o valor de X, em reais?
a) 200,00 b) 10.000,00 c) 10.200,00 d) 11.200,00 e) 12.000,00

49
Coletânea de Provas da CESGRANRIO
Assistente Administrativo – Casa da Moeda – CESGRANRIO – 2009
1) Manter uma televisão ligada três horas por dia, durante 30 dias, consome 9,9 kWh
de energia. Quantos kWh de energia serão consumidos por uma TV que permanecer
ligada quatro horas por dia, durante 20 dias?
(A) 6,6 (B) 6,8 (C) 7,2 (D) 8,8 (E) 9,2
2) “Essa semana, o Banco Central lançou campanha para que a população use mais
moeda e aprenda a
identificar notas falsas. Este ano, até agosto, foram apreendidas 251 mil notas falsas,
totalizando R$12.386.000,00. Desse valor, cerca de 10% correspondiam a notas de 20
reais.”
O Globo, 24 out. 2009 (Adaptado).
3) De acordo com essas informações, quantas notas falsas de 20 reais foram
apreendidas até agosto desse ano?
(A) Menos de 20 mil (B) Entre 20 mil e 40 mil (C) Entre 40
mil e 60 mil
(D) Entre 60 mil e 80 mil (E) Mais de 80 mil
4) Um comerciante aumento em 20% o preço de suas mercadorias. Com isso, as
vendas diminuíram, e ele resolveu oferecer aos clientes um desconto de 30% sobre o
preço com aumento. Desse modo, qual é, em reais, o preço com desconto de uma
mercadoria que inicialmente custava R$ 200,00?
(A) 144,00 (B) 168,00 (C) 180,00 (D) 188,00 (E) 196,00
5) Certo técnico de suporte em informática começou a resolver um problema em um
computador às 14h 40 min. Se ele levou 75 minutos para solucionar o problema, a que
horas ele terminou esse serviço?
(A) 16h 05min (B) 15h 55min (C) 15h 45min(D) 15h 35min(E) 15h 25min
6) Pedro possui 28 moedas, algumas de 50 centavos e outras, de 10 centavos. Se, ao
todo, Pedro tem R$ 6,00, quantas são as moedas de 50 centavos?
(A) 8 (B) 10 (C) 12 (D) 16 (E) 20
7) Uma máquina produz 1.200 peças em 4 horas. Quantas máquinas iguais a essa
devem funcionar juntas, durante 3 horas, para que sejam produzidas 8.100 peças no
total?
(A) 5 (B) 6 (C) 7 (D) 8 (E) 9
8) Ao receber seu décimo terceiro salário, Mário o dividiu em duas partes, diretamente
proporcionais a 4 e a 7. Ele depositou a menor parte na poupança e gastou o restante
em compras de Natal. Se Mário depositou R$ 560,00 na poupança, quanto ele
recebeu de décimo terceiro salário, em reais?
(A) 800,00 (B) 960,00 (C) 1.200,00 (D) 1.400,00 (E) 1.540,00
9) “Segundo a Unicef (Fundo das Nações Unidas para a Infância), menos da metade
da população mundial tem acesso à água potável. A irrigação corresponde a 73% do
consumo de água, 21% vai para a indústria e apenas 6% destina-se ao consumo
doméstico” (Disponível em: www.cetesb.sp.gov.br)
De acordo com as informações acima, de cada 2.000 litros de água, quantos litros se
destinam ao consumo doméstico?

50
(A) 120 (B) 210 (C) 420 (D) 600
(E) 1.200
10) Marcelo emprestou certa quantia a Augusto, cobrando juros simples de 4% ao
mês. Cinco meses mais tarde, Augusto pagou o empréstimo, e Marcelo recebeu R$
420,00. Qual foi, em reais, a quantia que Marcelo emprestou a Augusto?
(A) 320,00 (B) 336,00 (C) 350,00 (D) 382,00 (E) 400,00
11) A prateleira de certa estante suporta, no máximo, 8 kg. Um assistente
administrativo deseja arquivar algumas pastas. Quantas pastas ele poderá colocar
nessa prateleira sem ultrapassar sua capacidade máxima, se cada pasta pesa 350 g?
(A) 21 (B) 22 (C) 23 (D) 24 (E) 25
Assistente Administrativo – Casa da Moeda – CESGRANRIO – 2005
1) Considere as seguintes proposições:
I - o maior número inteiro negativo é -1;
II - dados os números inteiros -50 e -80, temos -50 < -80;
III - zero é um número racional.
Está(ão) correta(s) a(s) proposição(ões):
(A) II, apenas. (B) I, apenas. (C) I, II e III.
(D) I e II, apenas. (E) I e III, apenas.
2) As famílias de duas irmãs, Alda e Berta, vivem na mesma casa e a divisão das
despesas mensais é proporcional ao número de pessoas de cada família. Na família
de Alda são três pessoas e na de Berta, cinco. Se a despesa, num certo mês, foi de
R$ 1 280,00, quanto pagou, em reais, a família de Alda?
(A) 520,00 (B) 480,00 (C) 450,00 (D) 410,00 (E) 320,00
3) José viaja 350 quilômetros para ir de carro de sua casa à cidade onde moram seus
pais. Numa dessas viagens, após alguns quilômetros, ele parou para um cafezinho. A
seguir, percorreu o triplo da quantidade de quilômetros que havia percorrido antes de
parar. Quantos quilômetros ele percorreu após o café?
(A) 87,5 (B) 125,6 (C) 262,5 (D) 267,5 (E) 272,0
4) O preço de capa de uma revista semanal é de R$ 5,00. Na assinatura anual, com
direito a 12 edições dessa revista, há um desconto de 12%. O preço da assinatura, em
reais, é:
(A) 51,20 (B) 51,80 (C) 52,20 (D) 52,40 (E) 52,80
5) O quadro abaixo indica número de passageiros num voo entre Curitiba e Belém,
com duas escalas, uma no Rio de Janeiro e outra em Brasília. Os números positivos
indicam a quantidade de passageiros que subiram no avião e os negativos, a
quantidade dos que desceram em cada cidade.
O número de passageiros que chegou a Belém foi:
(A) 362 (B) 280 (C) 240 (D) 190 (E) 135

51
6) Para construir um piso de concreto, Antônio utiliza 50 kg de cimento para cada 2,50
m2 de piso. Quantos sacos com 50 kg de cimento serão necessários para que Antônio
possa cobrir uma superfície de 300 m2 ?
(A) 110 (B) 112 (C) 115 (D) 120 (E) 125
7) Uma pesquisa com duzentas pessoas concluiu que 3/4 delas são esportistas e 2/5
dos esportistas praticam natação. O número de pessoas que praticam natação é:
(A) 40 (B) 50 (C) 60 (D) 70 (E) 80
8) Um jogo com 4 tempos de mesma duração e 3 intervalos de 4 minutos cada um
leva duas horas. Quantos minutos de duração tem cada tempo desse jogo?
(A) 27 (B) 25 (C) 24 (D) 22 (E) 20
9) Um quintal pode ser ladrilhado com 200 ladrilhos de 250 cm2 de área, cada um.
Quantas lajotas de 400 cm2 , cada uma, são necessárias para recobrir o mesmo
quintal?
(A) 135 (B) 125 (C) 120 (D) 112 (E) 100
10) Pedro possui um terreno de 800 m2 e quer construir nele um canteiro que ocupe
20% da metade da área do terreno. Para isso contratou um jardineiro que cobrou R$
25,00 por m2 de canteiro construído. Quanto Pedro gastará, em reais?
(A) 2 400,00 (B) 2 300,00 (C) 2 250,00 (D) 2 120,00 (E) 2 000,00
Técnico em Economia – SEAD/AM – CESGRANRIO – 2005
1) Um fundo de investimento promete pagar 100% do CDI em regime de juros
compostos. A aplicação foi feita em outubro de 2004 e as taxas mensais do CDI
observadas são apresentadas na tabela abaixo:
Mês CDI (% ao ano)
Outubro/2004 16,41
Novembro/2004 16,96
Dezembro/2004 17,50
Janeiro/2005 17,93
Ao final de janeiro de 2005, o investidor sacou do fundo R$ 450.000,00. O
investimento inicial (em R$) foi:
(A) 289.313,26 (B) 336.951,45 (C) 394.564,11 (D) 426.813,70
(E) 487.515,20
2) Um indivíduo contratou uma dívida de R$ 35.000,00 junto a seu banco, pagando
juros simples de 32% ao ano para ser saldada em 36 prestações. Faltando 6 meses
para seu encerramento, o indivíduo decidiu liquidar a dívida. O desconto racional
obtido (em R$) foi:
(A) 4.563,12 (B) 4.699,99 (C) 4.748,45 (D) 4.827.59 (E) 4.981,24
3) Um investidor está considerando a compra de uma LTN de valor nominal igual a R$
1.000,00 e prazo de vencimento de 270 dias. Considerando-se o desconto racional
simples, que preço (em R$) deve pagar por este título para obter uma taxa de juros
anual de 20%?
(A) 833,33 (B) 869,57 (C) 872,20 (D) 983,61 (E) 999,44
4) No ano de 2004, a Taxa Selic média apurada foi 18,25% e a inflação, medida pelo
IPCA, foi 8,22%. A Selic real (em % ao ano) em 2004 foi:
(A) 0,45 (B) 1,50 (C) 2,22 (D) 9,26
(E) 10,03

52
5) A taxa de juros compostos mensal equivalente à taxa de 18,25% ao ano é:
(A) 4,56% (B) 4,28% (C) 3,00% (D) 1,52% (E) 1,41%
6) O valor presente (em R$) de uma série de 4 pagamentos mensais uniformes de R$
500,00, descontados à taxa anual de 26,82%, é igual a:
(A) 1.143,57 (B) 1.577,04 (C) 1.893,06 (D) 1.903,86 (E) 1.935,92
7) Um projeto com investimento inicial de R$ 50.000,00 e fluxos de caixa anual e
iguais a R$ 12.500,00 possui um período de payback (em anos) igual a:
(A) 5 (B) 4 (C) 3 (D) 2 (E) 1
Técnico Administrativo – BNDES – CESGRANRIO – 2013
1) Progressões aritméticas são sequências numéricas nas quais a diferença entre dois
termos consecutivos é constante. A sequência (5, 8, 11, 14, 17, ..., 68, 71) é uma
progressão aritmética finita que possui
(A) 67 termos (B) 33 termos (C) 28 termos (D) 23 termos (E) 21 termos
2) Dentro de um pote, há 5 bombons embrulhados em papel azul, 6 embrulhados em
papel vermelho, e 7 embrulhados em papel verde. Quantos bombons, no mínimo,
devem ser retirados do pote, sem que se veja a cor do papel, para se ter certeza de
haver retirado dois bombos embrulhados em papéis de cores diferentes.
(A) 3 (B) 4 (C) 6 (D) 7 (E) 8
3) Seja x um número natural tal que o mínimo múltiplo comum entre x e 36 é 360, e o
máximo divisor comum entre x e 36 é 12. Então, a soma dos algarismos do número x
é
(A) 3 (B) 5 (C) 9 (D) 16 (E) 21
4) Mariana e Laura compraram um saco com 120 balas que custava R$ 7,50. Laura
contribuiu com R$ 4,50, e Mariana, com o restante.Se as balas forem divididas em
partes diretamente proporcionais ao valor pago por cada menina, com quantas balas
Mariana ficará?
(A) 36 (B) 48 (C) 54 (D) 72 (E) 96
5) Uma empresa de propaganda pretende criar panfletos coloridos para divulgar certo
produto. O papel pode ser laranja, azul, preto, amarelo, vermelho ou roxo, enquanto o
texto é escrito no panfleto em preto, vermelho ou branco. De quantos modos distintos
é possível escolher uma cor para o fundo e uma cor para o texto se, por uma questão
de contraste, as cores do fundo e do texto não podem ser iguais?
(A) 13 (B) 14 (C) 16 (D) 17 (E) 18
4) Cem gramas de certo bolo têm 270 kcal. Pedro comeu 20g de bolo a mais que Vitor
e, ao todo, os dois ingeriram 376 kcal. Quantos gramas de bolo Pedro comeu?
(A) 55 (B) 60 (C) 75 (D) 80 (E) 90
5) Paulo aplicou R$ 10.000,00 em um fundo de investimentos que rendeu juros de 6%
em um ano. Ao término desse ano, Paulo manteve aplicados tanto os R$ 10.000,00
quanto os juros obtidos nesse primeiro ano e, ainda, aplicou mais R$ 4.400,00. Ele
deixou seu dinheiro investido por mais um ano e, ao final desses dois anos, seu saldo
(valor aplicado mais juros) foi de R$ 16.050,00. Sabendo-se que, ao longo desses dois
anos, Paulo não fez qualquer retirada, qual foi a taxa anual de juros no segundo ano?
(A) 5% (B) 6% (C) 7% (D) 8% (E) 9%

53
6) Um professor de ginástica estava escolhendo músicas para uma aula. As quatro
primeiras músicas que ele escolheu totalizavam 15 minutos, sendo que a primeira
tinha 3 minutos e 28 segundo de duração, a segunda 4 minutos e 30 segundos, e as
duas últimas, exatamente a mesma duração. Qual era a duração da terceira música?
(A) 3 min 1 s (B) 3 min 31 s (C) 3 min 51 s(D) 4 min 1 s (E) 4 min 11 s
7) Mário precisava resolver alguns exercícios de Matemática. Ele resolveu 1/5 dos
exe4rcícios no primeiro dia. No segundo dia, resolveu 2/3 dos exercícios restantes e,
no terceiro dia, os 12 últimos exercícios. Ao todo, quanto exercícios Mauro resolveu?
(A) 30 (B) 40 (C) 45 (D) 75 (E) 90
8) Em certa cidade, a tarifa do metrô é R$ 2,80, e a dos ônibus, R$ 2,40. Mas os
passageiros que utilizam os dois meios de transporte podem optar por um bilhete
único, que dá direito a uma viagem de ônibus e uma de metrô, e custa R$ 3,80. Em
relação ao valor total gasta como uma viagem de ônibus e uma de metrô pagas
separadamente, o bilhete único oferece um desconto de, aproximadamente,
(A) 27% (B) 30% (C) 32% (D) 34%
(E) 37%
9) O gráfico abaixo apresenta o consumo médio de oxigênio, em função do tempo, de
um atleta de 70 kg ao praticar natação
Considere que o consumo médio de oxigênio seja diretamente proporcional à massa
do atleta. Qual será, em litros, o consumo médio de oxigênio de um atleta de 80 kg,
durante 10 minutos de prática de natação?
(A) 50,0 (B) 52,5 (C) 55,00 (D) 57,5
(E) 60,00
10) O Parque Estadual Serra do Conduru, localizado no Sul da Bahia, ocupa uma área
de aproximadamente 9.270 hectares. Dessa área, 7 em cada 9 hectares são ocupados
por florestas. Qual é, em hectares, a área desses Parque NÃO ocupada por florestas?
(A) 2.060 (B) 2.640 (C) 3.210 (D) 5.100 (E) 7.210
11) Gilberto levava no bolso três moedas de R$ 0,50, cinco de R$ 01,0 e quatro de R$
0,25. Gilberto retirou do bolso oito dessas moedas, dando quatro para cada filho. A
diferença entre as quantias recebidos pelos dois filhos de Gilberto é de, no máximo,
(A) R$ 0,45 (B) R$ 0,90 (C) R$ 1,10 (D) R$ 1.15 (E) R $ 1,35
12) A força da água limpa. As novas tecnologias e o empenho dos organismos
públicos, associados aos interesses e boas práticas da iniciativa privada, ampliaram a
rede de esgotos.

54
Considere que, em 1990, a população brasileira era de 145 milhões de habitantes, em
2010, de 190 milhões. Com base nos percentuais apresentados na reportagem, o
número de habitantes, no Brasil, que contam com saneamento básico aumentou, de
1990 para 2010, em, aproximadamente,
(A) 65 milhões (B) 50 milhões (C) 45 milhões (D) 25 milhões
(E) 10 milhões
13) Multiplicando-se o maior número inteiro menor do que 8 pelo menor número inteiro
maior do que − 8, o resultado encontrado será
(A) – 72 (B) – 63 (C) – 56 (D) – 49
(E) − 42
14) Em uma faculdade, uma amostra de 120 alunos foi coletada, tendo-se verificado a
idade e o sexo desses alunos. Na amostra, apurou-se que 45 estão na faixa de 16 a
20 anos, 60, na faixa de 21 a 25 anos, e 15 na faixa de 26 a 30 anos. Os restados
obtidos encontram-se na Tabela abaixo.
Quais são, respectivamente, os valores indicados pelas letras P, Q, R e S?
(A) 40; 28; 64 e 0
(B) 50; 29; 64 e 7
(C) 50; 40; 53.3 e 7
(D) 77,8; 28; 53.3 e 7
(E) 77,8; 40; 64 e 0
15) João e Maria estão enfrentando dificuldades em algumas disciplinas do 1º ano do
Ensino Médio. A probabilidade de João ser reprovado é de 20%, e a de Maria é de
40%. Considerando-se que João e Maria são independentes, qual é a probabilidade
de que um ou outro seja reprovado?
(A) 0 (B) 0,2 (C) 0,4 (D) 0,52 (E) 0,6
16) Considere o seguinte conjunto: {15; 17; 21; 25; 25; 29; 33; 35}
A média, a mediana e a moda desse conjunto de dados são, respectivamente,
(A) 1, 2 e 3 (B) 5, 7 e 9 (C) 7, 9 e 5 (D) 25, 25 e 25 (E) 25, 27 e 29
17) Ricardo precisa escolher dois CD de seu acervo para tocar em uma festa. Ele tem
um CD de rock, dois de MPB, três de música clássica e dois de jazz. Se ele escolher

55
dois CD aleatoriamente, qual é a probabilidade de que os dois escolhidos sejam de
jazz ou de que um CD seja de MPB, e o outro, de música clássica?
(A) ½ (B) ¼ (C) 1/6 (D) 1/14 (E) 3/14
18) Em um departamento de uma empresa, o gerente decide dar um aumento a todos
os empregados, dobrando o salário de todos eles. Em relação às estatísticas dos
novos salários, considere as afirmativas abaixo.
I - A média dobra.
II - A variância dobra.
III - A moda dobra.
É correto o que se afirma em
(A) I, apenas (B) II, apenas (C) I e III, apenas (D) II e III, apenas
(E) I, II e III
Técnico Administrativo – BNDES – CESGRARIO – 2010
1) A 19ª Copa do Mundo de Futebol foi disputada na África do Sul, no dia 11 de junho
ao dia 11 de julho de 2010. Em todas as edições da Copa, durante a 1ª fase da
competição, cada seleção joga somente contra as equipes do grupo que integra, uma
única vez apenas contra cada uma delas. Na África do Sul, as 32 seleções
participantes foram divididas em 8 grupos de 4 equipes. Portanto, cada equipe jogou
uma única vez contra uma das outras 3 equipes de seu grupo. Assim, ao final da 1ª
fase, foram realizada ao todo, 48 jogos. Se a competição vier a ser disputada por 3
seleções divididas em 7 grupos de 5 equipes, ao final da 1ª fase, o número total de
jogos realizados será de:
(A) 35 (B) 70 (C) 92 (D) 105 (E) 140

56
2) Em uma caixa há 4 balas de mel, 3 balas de tamarindo e 3 balas de anis. Duas
balas serão retiradas aleatoriamente dessa caixa, sucessivamente e sem reposição.
Qual a probabilidade de que, pelo menos, uma das balas seja de mel?
(A) 3/5 (B) 2/5 (C) 2/3 (D) 1/3 (E) 1/12
3) Certa marca de café é comercializada exclusivamente em embalagens de 250 g ou
de 400 g. Se um consumidor dessa marca comprar uma embalagem de cada, gastará,
ao todo, R$ 3,30. Se, em vez disso, esse consumidor comprar o correspondente a 900
g em embalagens desse café, pagará, ao todo, R$ 4.60. A diferença, em reais, entre
os preços das embalagens de 400 g e de 250 g é
(A) 0,40 (B) 0,50 (C) 0,60 (D) 0,70
(E) 0,80
4) Quatro bombas d’água idênticas, trabalhando simultânea e ininterruptamente, são
capazes de encher completamente uma piscina em 5 h. Quando a piscina está
totalmente vazia, as quatro bombas são postas em funcionamento. Após 2h de
trabalho contínuo, uma enguiça. As outras três permanecem trabalhando, até que a
piscina esteja totalmente cheia. Quanto tempo, ao todo, é necessário para que a
piscina fique cheia?
(A) 5 horas e 30 minutos (B) 5 horas e 45 minutos (C) 6 horas (D) 6 horas e
30 minutos
5) Um jovem tinha um capital e fez com ele um investimento diversificado. Aplicou
40% do capital em um fundo de Renda Fixa e o restante na Bolsa de Valores. A
aplicação em Renda Fixa gerou lucro de 20%, enquanto o investimento na Bolsa, no
mesmo período, representou prejuízo de 10%. Com relação ao total investido nesse
período, o jovem
(A) teve lucro de 2% (B) teve lucro de 20% (C) não teve lucro e nem
prejuízo
(D) teve prejuízo de 2% (E) teve prejuízo de 20%
6) Uma aplicação consistente em 6 depósitos consecutivos mensais e iguais no valor
de R$ 300,00 (trezentos reais) cada um. Se a taxa de juros compostos utilizada é de
5% ao mês, o montante, em reais, um mês após o último dos 6 depositos é
(A) 2.040,00 (B) 2.142,00 (C) 2.240,00 (D) 2.304,00 (E) 2.442,00
7) A sequência numérica (6, 10, 14, ..., 274, 278, 282) tem 70 números, dos quais
apenas os três primeiros e os três últimos estão representados. Qualquer número
dessa sequência, executando-se o primeiro, é igual ao termo que o antecede mais 4.
A soma desses 70 números é
(A) 8.920 (B) 10.080 (C) 13.560 (D) 17.840 (E) 20.160
8) Dez mulheres adultas foram submetidas a uma pesquisa. A cada uma delas
perguntou-se: “Quantos filhos você tem?”. O entrevistador foi anotando cada uma das
respostas na ordem em que foram obtidas. No entanto, devido à pressa, esqueceu de
registrar uma das respostas. A listagem abaixo reproduz as respostas dadas, na
ordem em que foram registradas.
2 0 3 1 1 0 1 4 1
A partir das informações acima, analise as afirmativas a seguir.
I – A moeda das quantidade de filhos dessas dez mulheres independente da resposta
não registrada.
II – A mediana das quantidades de filhos dessas dez mulheres depende da resposta
não registrada.
III – A média das quantidades de filhos dessas dez mulheres independe da resposta
não registrada.

57
Está correto APENAS o que se afirma em:
(A) I. (B) II. (C) III. (D) I e II. (E) II e III.
9) A figura abaixo ilustra o gráfico da função que associa o volume do gás consumido
pelos domicílios de um município ao valor pago por esse consumo.
O valor pago, em reais, por cada metro cúbico consumido é de
(A) 7,00 (B) 5,60 (C) 5,00 (D) 4,20
(E) 4,00
10) Em uma pesquisa de preços de determinados produtos, foram obtidos os valores,
REM reais, de uma amostra aleatória, colhida em 6 estabelecimentos que o
comercializam.
A variância dessa amostra é
(A) 1,50 (B) 1,75 (C) 2,00 (D) 2,25 (E) 2,50
1) Aplicando-se R$5.000,00 a juros compostos, à taxa nominal de 24% ao ano, com
capitalização bimestral, o montante, em reais, ao fim de 4 meses, será
(A) 5.400,00 (B) 5.405,00 (C) 5.408,00 (D) 6.272,00 (E) 6.275,00
2) Considere que, em uma empresa, há máquinas copiadoras do tipo A e do tipo B,
nas seguintes condições:
* 3 máquinas do tipo A, funcionando conjuntamente com 2 máquinas do tipo B,
produzem 13.920 cópias, ao todo, em meia hora;
* todas as máquinas do tipo A funcionam sob um mesmo regime constante;
* todas as máquinas do tipo B funcionam sob um mesmo regime constante, 40% maior
do que o regime das máquinas do tipo A.
O número de cópias por minuto, nessa empresa, que uma máquina do tipo B faz a
mais do que uma máquina do tipo A é:
(A) 38 (B) 36 (C) 34 (D) 32 (E) 30
3) A metade de um capital C foi aplicada a juros compostos com taxa de 20% ao mês.
Simultaneamente, a outra metade foi aplicada a juros simples com taxa mensal de i%.
Ao final de dois meses, os montantes a juros simples e a juros compostos foram
somados e seu valor correspondia ao capital total C, acrescido de 50%. Quantos são
os divisores inteiros positivos de i ?
(A) 6 (B) 5 (C) 4 (D) 2 (E) 1

58
4) Uma seqüência de números (a1, a2, a3,...) é tal que a soma dos n primeiros termos
é dada pela expressão Sn = 3n2
+ n. O valor do 51º termo é:
(A) 300 (B) 301 (C) 302 (D) 303 (E) 304
5) Dois meses antes do seu vencimento, um título de valor nominal N sofrerá
desconto. Se o desconto for racional composto e a taxa utilizada for de 20% ao mês, o
valor do desconto será igual a d. Se o desconto for comercial composto, qual deverá
ser a taxa mensal de desconto para que o valor do desconto seja o mesmo?
(A) 83,3% (B) 69,1% (C) 42,8% (D) 20,0% (E) 16,7%
6) Em uma amostra de cinco residências de uma determinada rua, registram-se os
seguintes números de moradores em cada uma:
A variância amostral é
(A) 5,8 (B) 5,5 (C) 5,1 (D) 4,8 (E) 4,4
7) Seja X a variável que corresponde ao número de moradores em cada uma das 5
residências. Qual o gráfico da função de distribuição acumulada de X ?
8)Considerando-se que uma pessoa será escolhida ao acaso, qual a probabilidade de
que a sua idade esteja entre 28 e 36 anos, dado que a pessoa escolhida terá 24 anos
ou mais?

59
(A) 11/40 (B) 13/32 (C) 19/40 (D) 19/32 (E) 29/40
9)Seja μ e md, respectivamente, a média e a mediana das idades. O valor de μ – md
é
(A) 0,80 (B) 0,75 (C) 0,70 (D) 0,65 (E) 0,60
10) A distância interquartil é, aproximadamente,
(A) 6,3 (B) 6,5 (C) 6,7 (D) 6,9 (E) 7,1
11) A tabela a seguir apresenta dados sobre a evolução de preços e quantidades de
dois produtos, em dois anos consecutivos.
Com base nos dados apresentados, em relação ao nível de preços dos dois produtos,
os índices de Paasche e de Laspeyres, respectivamente, indicam
(A) a sua manutenção e uma redução de 12%.
(B) a sua manutenção e um aumento de 12%.
(C) uma redução de 12% e um aumento de 12%.
(D) uma redução de 12% e a sua manutenção.
(E) um aumento de 12% e a sua manutenção.
12) Considere a seqüência de figuras apresentada a seguir.
Essa seqüência de figuras segue o padrão lógico de um sistema de numeração. De
acordo com esse padrão, a próxima figura será
1) Para um determinado bem, o relativo de preços de março em relação a fevereiro foi
igual a 1,25. Portanto, o relativo de preços de fevereiro desse bem, em relação a
março, vale:
(A) 0,75 (B) 0,80 (C) 1,00 (D) 1,20 (E) 1,25
2) Se a média aritmética dos valores de X é 2, quanto vale a média dos valores de Y =
2X+1?
(A) 4 (B) 5 (C) 6 (D) 8 (E) 9
3) O número de soluções inteiras do sistema de inequações
4) Quantos litros há em 1m3
?
(A) 1 (B) 10 (C) 100 (D) 1 000 (E) 10 000

60
5) Um artigo, cujo preço à vista é R$ 210,00, pode ser comprado a prazo com dois
pagamentos iguais: o primeiro no ato da compra e o segundo um mês após. Se os
juros são de 10% ao mês, qual é o valor, em reais, de cada pagamento?
(A) 110,00 (B) 115,50 (C) 121,00 (D) 126,00 (E) 130,00
6) O valor de x no sistema
é
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
7) Em uma empresa, a razão do número de empregados homens para o de mulheres
é 3/7. Portanto, a porcentagem de homens empregados nessa empresa é:
(A) 30% (B) 43% (C) 50% (D) 70% (E) 75%
8) Quantos são os números inteiros, compreendidos entre 100 e 200, que são
múltiplos de 3 e, simultaneamente, não são múltiplos de 5?
(A) 13 (B) 16 (C) 21 (D) 26 (E) 27
Técnico Bancário – Banco da Amazônia – CESGRANRIO – 2013
1) Considere duas alternativas de investimento, X e Y, mutuamente exclusivas, com o
fluxo de caixa apresentado a seguir.
Os métodos do valor presente líquido, VPL, e o da taxa interna de retorno, TIR, são
métodos tradicionais na análise de investimentos. Os projetos X e Y possuem taxa
interna de retorno, TIR, de 13,6% e 13,9%, ao ano, respectivamente. Considerando
apenas projetos viáveis, os métodos podem levar a decisões divergentes, dependendo
do valor considerado para a taxa mínima de atratividade, ou seja, existe um valor para
a taxa mínima de atratividade abaixo do qual os métodos levam a decisões
divergentes, e acima do qual as decisões encaminhadas pelos métodos
convergem.Tal valor é
(A) 100/11 % ao ano (B) 100/9 % ao ano (C) 100/13% ao ano (D) 13,6% ao ano (E)
13,9% ao ano
2) Um empréstimo deverá ser pago em quarenta e nove prestações mensais e
consecutivas, vencendo a primeira prestação trinta dias após a liberação do dinheiro.
O financiamento foi feito pelo Sistema de Amortização Constante, SAC, com taxa
mensal de juros de 1%. Se a vigésima quinta prestação é de R$ 5.000,00, o saldo
devedor, em reais, após o pagamento da quadragésima oitava prestação é de:
(A) 4.000 (B) 4.080 (C) 4.800 (D) 4.880 (E) 5.000
3) Uma revista acadêmica publicou um artigo no qual estava inserida a Tabela a
seguir.

61
A melhor estimativa para a média do rendimento mensal, em salários mínimos, é
(A) 2,05 (B) 2,15 (C) 2,35 (D) 2,45 (E) 2,65
4) A Tabela a seguir apresenta a distribuição dos clientes de uma determinada
agência bancária classificados segundo o perfil do investidor em: conservadores,
moderados e arrojados
Considere as medidas estatísticas: média, moda, mediana, variância e desvio padrão.
Para análise da classificação dos clientes, é possível determinar a
(A) moda, apenas (B) média e a mediana, apenas (C) média, a
moda e a mediana, apenas
(D) média, a variância e o desvio padrão, apenas (E) média, a moda, a mediana, a
variância e o desvio padrão
5) A sequência na, nϵIN, é uma progressão aritmética cujo primeiro termo é a1=-2 e
cuja razão é r=3. Uma progressão geométrica, bn, é obtida a partir da primeira, por
meio da relação bn=3an
, nϵIN. Se b1 e q indicam o primeiro termo e a razão dessa
progressão geométrica, então q/b1 vale:
(A) 243 (B) 3 (C) 1/243 (D) -2/3 (E) -
27/6
6) As capitalizações oferecidas por dois fundos de investimento foram simuladas por
uma operadora financeira. A aplicação inicial em ambos os fundos foi a mesma. Na
simulação, a capitalização no primeiro fundo de investimento durou 48 meses e se deu
a juros mensais de 1%, no regime composto. No segundo fundo de investimento, a
capitalização durou 24 meses apenas. A operadora buscava determinar qual deveria
ser a taxa mensal de juros oferecida pelo segundo fundo, em regime composto, para,
ao final dos 24 meses, gerar o mesmo montante gerado pelo primeiro ao final dos 48
meses. Essa taxa é de
(A) 2% a.m. (B) 2,01% a.m. (C) 2,02% a.m. (D) 2,1% a.m.
(E) 2,2% a.m.
7) Um refrigerador custa, à vista, R$ 1.500,00. Um consumidro optou por comprá-lo
em duas parcelas. A loja cobra uma taxa mensal de juros (compostos) de 2%, atuante
a partir da data da compra. O valor da primeira parcela, paga pelo consumidor 30 dias
após a compra, foi de R$ 750,00. Um mês após o primeiro pagamento, o consumidro
quitou sua dívida ao pagar a segunda parcela. Qual foi o valor da segunda parcela?
(A) R$ 750,00 (B) R$ 765,00 (C) R$ 780,00 (D) R$ 795,60
(E) R$ 810,00

62
8) A Figura apresenta uma região do plano cartesiano, destacada na cor cinza, que é
limitada por uma reta e por uma parábola. A região em destaque é constituída pelos
pontos (x,y) cujas coordenadas satisfazem o seguinte sistema de inequações:
9) Sabe-se que x e y são números reais tais que y = 53x
Conclui-se que x é igual a
10) Os comprimentos de uma mesa e de uma bancada são, respectivamente, iguais a
204 centímetros e 7,5 metros. A razão entre o comprimento da mesa e o comprimento
da bancada, quando ambos são escritos em uma mesma unidade, é
(A) 17/625 (B) 5/136 (C) 68/125 (D) 34/125 (E) 136/5
Técnico Bancário – CEF – CESGRANRIO – 2008
Para responder às questões de nos 1 e 2, utilize os dados da tabela abaixo, que
apresenta as freqüências
acumuladas das idades de 20 jovens entre 14 e 20 anos.
1) Um desses jovens será escolhido ao acaso. Qual a probabilidade de que o jovem
escolhido tenha menos de 18 anos, sabendo que esse jovem terá 16 anos ou mais?
(A) 8/14 (B) 8/16 (C) 8/20 (D) 3/14 (E) 3/16
2) Uma das medidas de dispersão é a variância populacional, que é calculada por
. Sabendo-se que m é a média aritmética dessas idades, qual a variância
das idades na população formada pelos 20 jovens?
(A) 0,15 (B) 0,20 (C) 1,78 (D) 3,20 (E) 3,35
3)

63
Qual é o 70º termo da seqüência de números (an) definida acima:
(A) 2 (B) 1 (C) -1 (D) -2 (E) -3
4) A tabela abaixo apresenta o fluxo de caixa de um certo projeto.
A taxa interno de retorno é igual a
(A) 10% (B) 15% (C) 20% (D) 12%
(E) 18%
5) Quantos números múltiplos de 7 ou de 11 há entre 1 e 1000?
(A) 90 (B) 142 (C) 220 (D) 229 (E) 232
6) Considere um número N com exatamente dois algarismos diferentes de zero, e seja
P o conjunto de todos os números distintos de dois algarismos formados com os
algarismos de N, incluindo o próprio N. A soma de todos os números doconjunto P,
qualquer que seja N, é divisível por
(A) 2 (B) 3 (C) 5 (D) 7 (E) 11
7) Um empréstimo de R$ 200,00 será pago em 4 prestações mensais, sendo a
primeira delas paga 30 dias após o empréstimo, com juros de 10% ao mês, pelo
Sistema de Amortização Constante (SAC). O valor, em reais, da terceira prestação
será
(A) 50,00 (B) 55,00 (C) 60,00 (D) 65,00 (E) 70,00
8) Qual a taxa efetiva semestral, no sistema de juros compostos, equivalente a uma
taxa nominal de 40% ao quadrimestre, capitalizada bimestralmente?
(A) 75,0% (B) 72,8% (C) 67,5% (D) 64,4% (E) 60,0%
9) O gráfico a seguir representa as evoluções no tempo do Montante a Juros Simples
e do Montante a Juros Compostos, ambos à mesma taxa de juros. M é dado em
unidades monetárias e t, na mesma unidade de tempo a que se refere a taxa de juros
utilizada.
Analisando-se o gráfico, conclui-se que para o credor é mais vantajosos emprestar a
juros
(A) compostos, sempre
(B) compostos, se o período do empréstimo for menor do que a unidade de tempo
(C) simples, sempre
(D) simples, se o período do empréstimo for maior do que a unidade de tempo
(E) simples, se o período do empréstimo for menor do que a unidade de tempo

64
10) Um título de valor nominal R$ 24.200,00 será descontado dois meses antes do
vencimento, com taxa composta de desconto de 10% ao mês. Sejam D o valor do
desconto comercial composto e d o valor do desconto racional composto. A diferença
D – d, em reais, vale
(A) 399,00 (B) 398,00 (C) 397,00 (D) 396,00 (E) 395,00
Técnico Bancário - Administrativo – Caixa – CESGRANRIO – 2008
1) Em uma urna há 5 bolas verdes, numeradas de 1 a 5, e 6 bolas brancas,
numeradas de 1 a 6. Dessa urna retiram-se, sucessivamente e sem reposição, duas
bolas. Quantas são as extrações nas quais a primeira bola sacada é verde e a
segunda contém um número par?
(A) 15 (B) 20 (C) 23 (D) 25 (E) 27
2) Após a data de seu vencimento, uma dívida é submetida a juros compostos com
taxa mensal de 8%, além de ser acrescida de uma multa contratual correspondente a
2% da dívida original. Sabendo-se que log2=0,30 e log3=0,48 e utilizando-se para todo
o período o sistema de capitalização composta, determine o tempo mínimo necessário
em meses, para que o valor a ser quitado seja 190% maior do que a dívida original.
(A) 24 (B) 23,5 (C) 13 (D) 11,5 (E) 10
3)

65
Em um caminho retilíneo há um canteiro formado por 51 roseiras, todas enfileiradas ao
longo do caminho como ilustrado. A distância entre quaisquer duas roseiras
consecutivas é 1,5 m. Nesse caminho, há ainda uma torneira a 10,0 m da primeira
roseira. Gabriel decide molhar todas as roseiras desse caminho. Para isso, utiliza um
regador que, quando cheio, tem capacidade para molhar 3 roseiras. Dessa forma,
Gabriel enche o regador na torneira, encaminha-se para a 1ª roseira, molha-a,
caminha até a 2ª roseira, molha-a e, a seguir, caminha até a 3ª roseira, molhando-a
também, esvaziando o regador. Cada vez que o regador fica vazio, Gabriel volta à
torneira, enche o regador e repete a rotina anterior para as três roseira seguintes. No
momento em que acabar de regar a última das roseiras, quantos metros Gabriel terá
percorrido ao todo desde que encheu o regador pela primeira vez?
(A) 1666,0 (B) 1581,0 (C) 1496,0 (D) 833,0
(E) 748,0
4) Um investimento consiste na realização de 12 depósitos mensais de R$ 100,00,
sendo o primeiro deles feito um mês após o início da transação. O montante será
resgatado um mês depois do último depósito. Se a taxa de remuneração do
investimento é de 2% ao mês, no regime de juros compostos, o valor do resgate, em
reais, será
(A) 1200,00 (B) 1224,00 (C) 1241,21 (D) 1368,03
(E) 2128,81
5) A taxa efetiva anual de 50%, no sistema de juros compostos, equivale a uma taxa
nominal de i % ao semestre, capitalizada bimestralmente. O número de divisores
inteiros positivos de i é
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
6) A tabela abaixo apresenta o fluxo de caixa de um certo projeto.
Para que a taxa interna de retorno anual seja 5%, o valor de P, em milhares de reais,
deve ser
(A) 216,5 (B) 217,5 (C) 218,5 (D) 219,5 (E) 220,5
7) Um empréstimo de R$ 300,00 será pago em 6 prestações mensais, sendo a
primeira delas paga 30 dias após o empréstimo, com juros de 4% ao mês sobre o
saldo devedor, pelo Sistema de Amortização Constante (SAC). O valor, em reais, da
quarta prestação será
(A) 50,00 (B) 52,00 (C) 54,00 (D) 56,00 (E) 58,00
8) Joga-se N vezes um dado comum, de seis faces, não-viciado, até que se obtenha 6
pela primeira vez. A probabilidade de que N seja menor do que 4 é
(A) 150/216 (B) 91/216 (C) 75/216 (D) 55/216
(E) 25/216
9) Júlio fez uma compra de R$ 600,00, sujeita à taxa de juros de 2% ao mês sobre o
saldo devedor. No ato da compra, fez o pagamento de um sinal no valor de R$ 150,00.
Fez ainda pagamentos de R$ 159,00 e R$ 206,00, respectivamente, 30 e 60 dias
depois de contraída a dívida. Se quiser quitar a dívida 90 dias depois da compra,
quanto deverá pagar, em reais?
(A) 110,00 (B) 106,00 (C) 108,00 (D) 104,00
(E) 102,00

66
10) Escrevendo-se todos os números inteiros de 1 a 1111, quantas vezes o algarismo
1 é escrito?
(A) 481 (B) 420 (C) 448 (D) 300
(E) 289
Técnico Bancário Novo – Caixa – CESGRANRIO – 2013
1) Um imóvel de 100 mil reais é financiado em 360 prestações mensais, a uma taxa de
juros de 1% ao mês, pelo Sistema de Amortização Francês (Tabela Price), gerando
uma prestação de R$ 1.028,61. Reduzindo-se o prazo do financiamento para 240
prstações, o valor de cada prestação é, em reais, aproxidamente,
Dado, (1,01)-120
=0,3
(A) 1.099,00 (B) 1.371,00 (C) 1.428,00 (D) 1.714,00
(E) 2.127,00
2) Um projeto de investimento, cujo aporte de capital inicial é de R$ 20.000,00, irá
gerar, após um período, retorno de R$ 35.000,00. A Taxa Interna de Retorno (TIR)
desse investimento é
(A) 34% (B) 43% (C) 75% (D) 175%
(E) 275%
3) Nas operações de empréstimo, uma financeira cobra taxa efetiva de juros, no
regime de capitalização composta, de 10,25% ao ano. Isso equivale a cobrar juros
com taxa anual e capitalização semestral de
(A) 5% (B) 5,51% (C) 10% (D) 10,25%
(E) 10,51%
4) O montante gerado por uma instituição financeira, em uma aplicação no regime de
juros compostos, é R$ 5.000,00, em 10 meses, ou R$ 5.202,00, em 1 ano. Se a taxa
de juros é constante, o valor aplicado é, em reais, de, aproximadamente
(A) 1.950 (B) 3.100 (C) 3.400 (D) 3.950
(E) 4.100

67
Sumário
MATEMÁTICA COMERCIAL............................................................................................................ 3
Razão e Proporção .................................................................................................................... 3
Divisão Proporcional ................................................................................................................. 4
Regra de Sociedade Simples...................................................................................................... 5
Regra de Três Simples ............................................................................................................... 8
Regra de Três Composta ........................................................................................................... 8
Porcentagem............................................................................................................................. 9
Juros Simples........................................................................................................................... 13
Desconto Simples.................................................................................................................... 16
Desconto Composto................................................................................................................ 17
Taxas........................................................................................................................................ 17
MATEMÁTICA FINANCEIRA ......................................................................................................... 19
Observações sobre o uso da calculadora financeira HP-12C.................................................. 19
Financiamento e Aplicações.................................................................................................... 21
Empréstimos e Sistemas de Amortização............................................................................... 32
OUTROS TEMAS EM MATEMÁTICA FINANCEIRA.................................................................... 36
Questões da CESGRANRIO .......................................................................................................... 40
PROVA DO BANCO DO BRASIL – ESCRITURÁRIO – CESGRANRIO – 2012................................ 40
PROVA DO BANCO DO BRASIL – ESCRITURÁRIO – CESGRANRIO – 2010................................ 43
QUESTÕES DA CESGRANRIO – 2011 A 2013 – RENDAS CERTAS, FINANCEIRAS OU ANUIDADES
................................................................................................................................................. 45
Coletânea de Provas da CESGRANRIO..................................................................................... 49
ESSE CURSO É UMA VERSÃO ‘BETA’, NÃO CORRIGIDA E COM PROVÁVEIS
ERROS. ELE SÓ SERVE PARA O CURSO QUE SERÁ MINISTRADO PELO PROF.
OTÁVIO EM MUZAMBINHO NOS DIAS 1, 2 E 8 DE FEVEREIRO DE 2014

Curso 2 bb

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Curso 2 bb

Mais de Otávio Sales

Último

Curso 2 bb