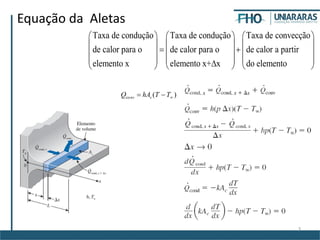
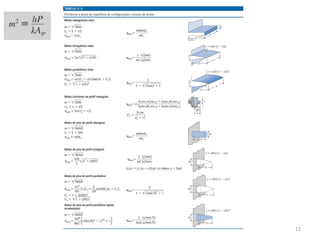
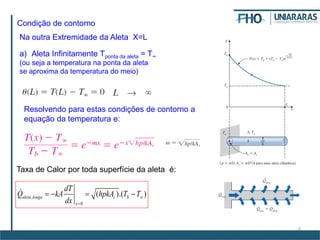
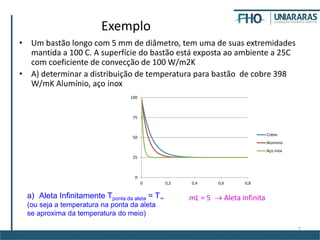
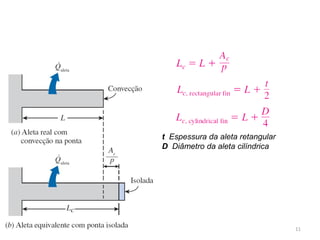
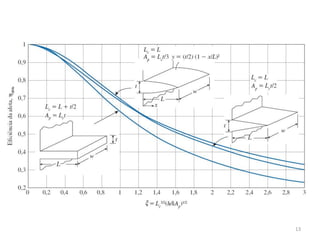
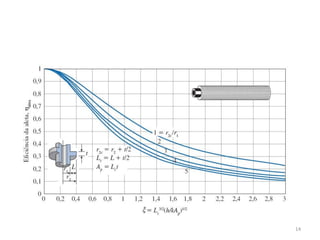
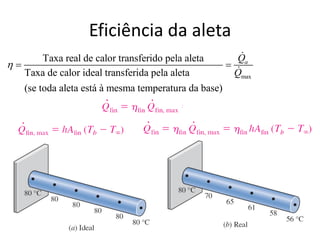
1. O documento apresenta equações para modelar a transferência de calor em aletas. Inclui equações para aletas retangulares, cilíndricas e infinitamente longas. 2. São apresentadas condições de contorno para diferentes configurações de aletas e soluções para as equações diferenciais correspondentes. 3. O documento discute parâmetros que afetam a eficiência e efetividade de aletas, como condutividade térmica, geometria, coeficiente de transferência de calor.

1. 1
Superfícies Estendidas – Aletas

2. 2

3. 3
Equação da Aletas
Taxa de condução Taxa de condução Taxa de convecção
de calor para o de calor para o de calor a partir
elemento x elemento x+ x do elemento
     
     
      
          
co ( )nv sQ hA T T 

4. 4
2
2
(condutividade térmica) constante
(Área da seção transversal) constante
( ) 0
( ) 0
c
c
c
k
A
d dT hp
T T
dx dx kA
d T hp
T T
dx kA




 
   
 
  
2 2
2 2
2
( ) ( )
( )
( )
c
Mudança de Variável
T x T x
dT d x
dx dx
d T d x
dx dx
e Chamando
hp
m
kA



 



2
2
2
0
d
m
dx

 
A solução geral da equação
diferencial é:

5. 5
2
2
2
0
d
m
dx

 
A solução geral da equação
diferencial é:
Condição de contorno
Na Base da Aleta X=0

6. 6
Condição de contorno
Na outra Extremidade da Aleta X=L
a) Aleta Infinitamente Tponta da aleta = T∞
(ou seja a temperatura na ponta da aleta
se aproxima da temperatura do meio)
Resolvendo para estas condições de contorno a
equação da temperatura e:
Taxa de Calor por toda superfície da aleta é:
,
0
( ).( )aleta longa c b
x
dT
Q kA hpkA T T
dx


   

7. 7
Exemplo
• Um bastão longo com 5 mm de diâmetro, tem uma de suas extremidades
mantida a 100 C. A superfície do bastão está exposta ao ambiente a 25C
com coeficiente de convecção de 100 W/m2K
• A) determinar a distribuição de temperatura para bastão de cobre 398
W/mK Alumínio, aço inox
0
25
50
75
100
0 0,2 0,4 0,6 0,8
Cobre
Aluminio
Aço Inox
mL = 5  Aleta infinitaa) Aleta Infinitamente Tponta da aleta = T∞
(ou seja a temperatura na ponta da aleta
se aproxima da temperatura do meio)

8. 8
b) Taxa Perda de calor desprezível na ponta da aleta Qponta da aleta = 0
(Como a área da ponta é muito pequena e a transferência de calor é
proporcional a área essa é uma aproximação razoável para uma aleta
não tão longa)
Condição de contorno
Variação da temperatura
Taxa de Calor por toda superfície da aleta é:
0
( ).( )tanhaleta c b
x
dT
Q kA hpkA T T mL
dx


   

9. 9
Exemplo
• Determine o erro % entre uma aleta fixa a superfície considerando a
comprimento longo b) sem perda de calor na extremidade
_
0
( ).( )aleta longa c b
x
dT
Q kA hpkA T T
dx


   
_
0
( ).( )tanhaleta isolada c b
x
dT
Q kA hpkA T T mL
dx


   
_ _
_
( ).( ) ( ).( )tanh 1
% 1
tanh( ).( )tanh
aleta longa aleta isolada c b c b
aleta isolada c b
Q Q hpkA T T hpkA T T mL
Erro
mLQ hpkA T T mL
 

   
   

2
1
2
(12 / ) (0.0004 )
7,116
(237 / ) (0,004 ) / 4c
hp W m C m
m m
kA W m C m



 

 
1 1
% 1 1 0,635 63,5%
tanh tanh (7,116)(0,10)
Erro
mL
     

10. 10
c) Convecção na ponta da aleta
( é a condição de contorno mas realista
Condição de contorno
Variação da temperatura
Taxa de Calor por toda superfície da aleta é:
( ) cosh ( ) ( / ) ( )
cosh( ) ( / )b
T x T m L x h mk senhm L x
T T mL h mk senhmL


   

 
0
( ) ( / )cosh
( ).( )
cosh( ) ( / )
aleta c b
x
dT senh mL h mk mL
Q kA hpkA T T
dx mL h mk senhmL



   


11. 11
t Espessura da aleta retangular
D Diâmetro da aleta cilíndrica

12. 12

13. 13

14. 14

15. Eficiência da aleta
15
max
Taxa real de calor transferido pela aleta
Taxa de calor ideal transferida pela aleta
(se toda aleta está à mesma temperatura da base)
aQ
Q
  

16. Efetividade da aleta
16
b
b
Calor transferido a partir de
uma aleta de área da base A
Calor Transferido de uma ( )
superfície de área da base A
aleta aleta
semaleta b b
Q Q
Q h A T T


  

( )
( ) ( )
aleta aleta aleta aleta b
semaleta b b b b
aleta
aleta
b
Q Q h A T T
Q h A T T h A T T
A
A


 

 

  
 


17. Exemplo
17
( )
( )
c baleta
semaleta b b
c
b
c b
hpkA T TQ kp
Q h A T T hAc
k Condutividade Térmica
p Perímetro
h CoeficientedeTroca decalor convectivo
A Área da seçãotransversal
A Área dabase
A A
 


  







Qual a efetividade de uma aleta infinita de seção transversal uniforme
,inf
0
( ).( )aleta inita c b
x
dT
Q kA hpkA T T
dx


   

18. Algumas conclusões
18
( )
( )
c baleta
semaleta b b
hpkA T TQ kp
Q h A T T hAc
 


  

1. k ↑ ε ↑
2. p/Ac ↑ ε ↑ - Chapas finas e aletas delgadas na forma de pinos
3. h ↓ ε ↑ - Melhor em Gás do que em líquidos, convecção
natural que forçada
Ex. num trocado de calor gás - líquido como radiador de um carro as
aletas são instaladas no lado do gás (ar).

19. Tamanho adequado da
aleta
19
0
( ).( )tanhaleta c b
x
dT
Q kA hpkA T T mL
dx


   
,
0
( ).( )aleta longa c b
x
dT
Q kA hpkA T T
dx


   
,
,
( ).( )tanh( )
tanh( )
( ).( )
aleta c b
aleta longa c b
Q hpkA T T mL
mL
Q hpkA T T



 

mL Tanh(mL)
0,1 0,1
0,2 0,197
0,5 0,467
1 0,762
1,5 0,905
2 0,964
2,5 0,987
3 0,995
4 0,999
5 1,00

20. Superfície com varias aletas
20
( ) ( )
( )( )
total não aletada aleta
nãoaletada b aleta aleta b
nãoaletada aleta aleta b
Q Q Q
hA T T hA T T
h A A T T


 

 
   
  
( )( )
( )
total aleta não aletada aleta aleta b
global
total sem aleta sem aleta b
Q h A A T T
Q hA T T

 

 
 


21. Lista de Exercícios
1- Uma aleta retangular de 0,002 x 0,02 m k= 50 W/mK está numa parede e troca calor com ar h=600
W/m2K, T∞= 20 °C , sabendo que Tb= 170 °C. Qual o fluxo de calor e sua eficácia.
2-Considere uma aleta retangular muito longa fixada à superfície plana de tal forma que a temperatura na
sua ponta seja essencialmente a mesma do ar circundante , 20˚C, sua largura é5 cm e espessura 1,0 mm, k –
20W/mK e a temperatura na base 40 ˚C, o coeficiente de transferência de calor convectivo h=20W/m^2K.
Estime a temperatura a distancia de 5 cm da base da aleta e a taxa de perda de calor.
3- Uma aleta plana fabricada com a liga de alumínio 2024 (k = 185 W/(m · K)) tem uma espessura na base de t
= 3 mm e um comprimento de 15 mm. Sua temperatura na base é Tb = 100°C e ela está exposta a um fluido
no qual T∞ = 20°C e h = 50 W/(m2 · K). Para as condições anteriores e uma aleta de largura unitária, compare
a taxa de transferência de calor na aleta, a eficiência e para os perfis retangular, triangular e parabólico
4-Uma lamina de turbina feita de liga de metal (K=14W/mK) tem comprimento de 5,3 cm perímetro de 11 cm
e área transversal de 5,1 cm^2. A lamina da turbina e exposta aos gases quente da câmera de combustão a
973°C com coeficiente de transferência de calor h=538 W/m2K. A base da lamina da turbina mantém
temperatura de 450 °C. Determine a taxa de transferência de calor para a lamina e a temperatura na ponta da
turbina
5- uma parede plana com temperatura de 350°C está ligada a aletas retangulares retas k=235 w/mK, as aletas
são expostas ao ar ambiente a 25°C e o coeficiente de transferência de calor convectivo h = 154 W/m2K. Cada
aleta tem 50mm de largura , 5 mm de espessura e 100 mm de comprimento. Determine a eficiência da aleta
, a efetividade, e a taxa de transferência de calor pelo método gráfico e pelas equações da tabela
6- assumindo uma aleta de k=180 W/mK, t=3 mm L=15 mm e tb=100°Ce T∞ =25°C h =50 W/m2K e largura
unitária De termine a taxa de transferência de calor para uma aleta com perfil a) Retangular b) triangular )
parabólico
21