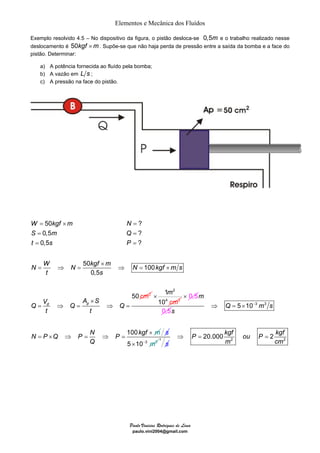
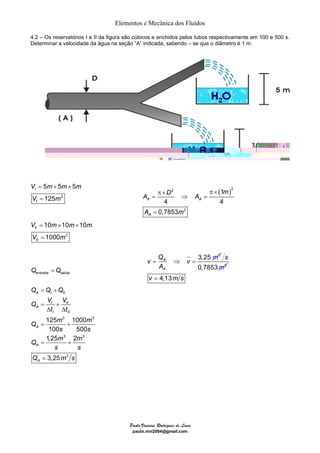
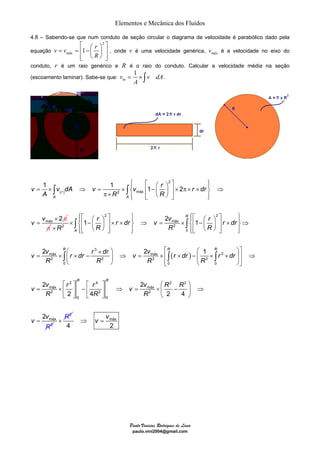
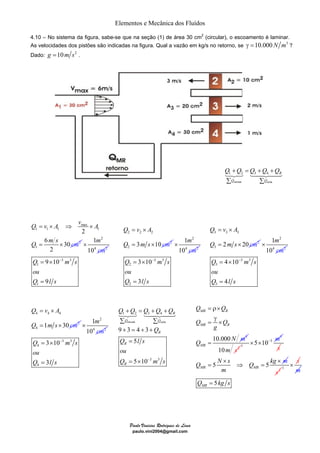
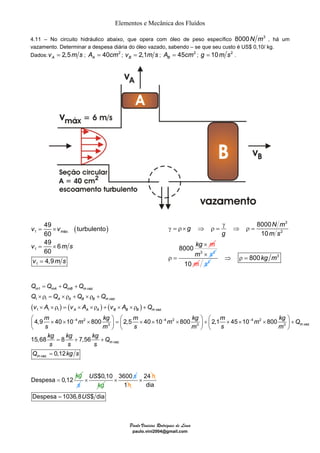
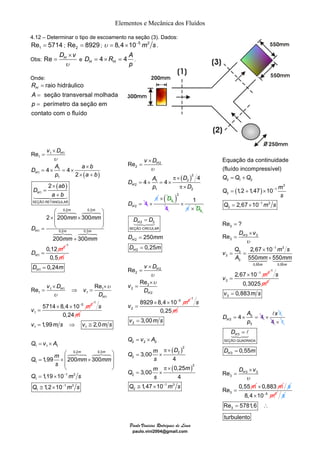
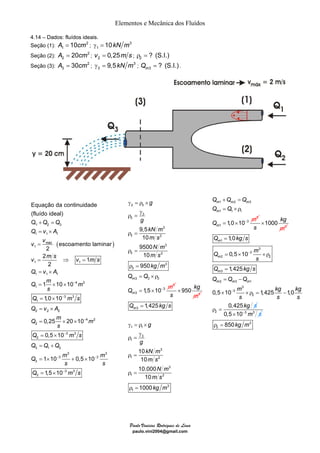
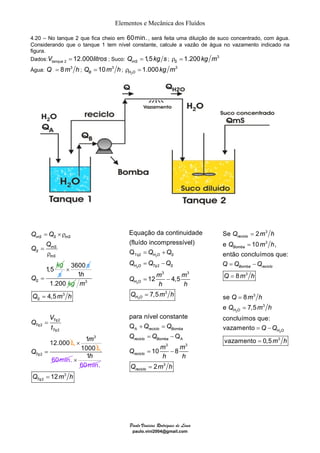
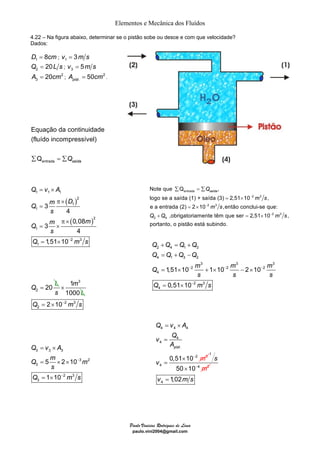
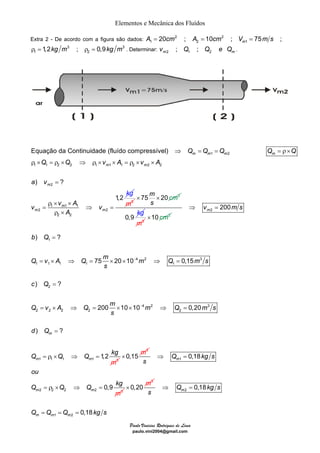
O documento discute quatro exemplos de problemas envolvendo elementos e mecânica dos fluidos. O primeiro exemplo calcula a vazão e velocidade em uma seção de um tubo, sabendo que o fluido é água e incompressível. O segundo exemplo resolve um problema similar considerando um fluido compressível, ar. O terceiro exemplo calcula a massa específica, vazão e velocidade de uma mistura homogênea de água e óleo. O quarto exemplo determina a velocidade dos gases de escape de um jato, dado a taxa de combustível queimado e