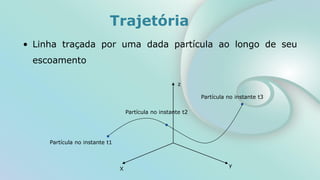
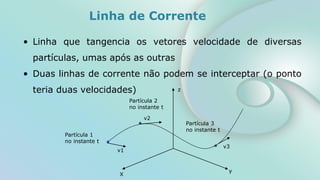
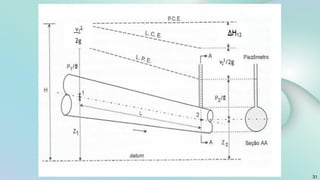
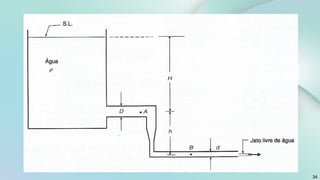
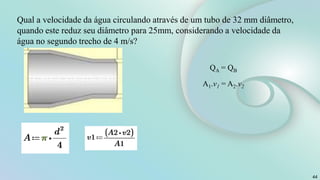
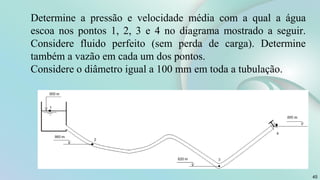
O documento aborda conceitos fundamentais sobre escoamento de fluidos, incluindo definições de escoamentos laminar e turbulento, bem como as características do experimento de Reynolds que ilustra esses regimes. Além disso, explora a vazão volumétrica, a equação da continuidade e a equação de Bernoulli para um escoamento permanente de fluidos incompressíveis. O documento também apresenta exemplos práticos e cálculos relacionados à pressão e velocidade em sistemas de tubulação.

1. FENOMENOS DE
TRANSPORTE
Patrício gomes leite
Aula 3

2. O que é escoamento?
• Mudança de forma do fluido sob a ação de um esforço
tangencial;
• Fluidez: capacidade de escoar, característica dos fluidos;
• Processo de movimentação das moléculas de um fluido,
umas em relação às outras e aos limites impostos

3. Escoamentos
• Os escoamentos são descritos por:
– Parâmetros físicos
– Pelo comportamento destes parâmetros ao longo do
espaço e do tempo;

4. Trajetória
• Linha traçada por uma dada partícula ao longo de seu
escoamento
X
y
z
Partícula no instante t1
Partícula no instante t2
Partícula no instante t3

5. Linha de Corrente
• Linha que tangencia os vetores velocidade de diversas
partículas, umas após as outras
• Duas linhas de corrente não podem se interceptar (o ponto
teria duas velocidades)
X
y
z
Partícula 1
no instante t
Partícula 2
no instante t
Partícula 3
no instante t
v1
v2
v3

6. Tubo de Corrente
• No interior de um fluido em
escoamento existem infinitas
linhas de corrente definidas por
suas partículas fluidas
• A superfície constituída pelas
linhas de corrente formada no
interior do fluido é denominada de
tubo de corrente ou veia líquida

7. Linha de Emissão
• Linha definida pela sucessão de
partículas que tenham passado
pelo mesmo ponto;
• A pluma que se desprende de
uma chaminé permite
visualizar de forma grosseira
uma linha de emissão;
Ponto de
Referência

8. •Escoamento Tridimensional:
– As grandezas que regem o escoamento variam nas três dimensões.
•Escoamento Bidimensional:
– As grandezas do escoamento variam em duas dimensões ou são
tridimensionais com alguma simetria.
•Escoamento Unidimensional:
–São aqueles que se verificam em função das linhas de corrente (uma
dimensão).
Classificação Geométrica do
Escoamento

9. • Permanente:
– Todas as propriedades e grandezas características do
escoamento são constantes no tempo;
• Não Permanente:
– Quando ao menos uma grandeza ou propriedade do fluido
muda no decorrer do escoamento;
Classificação do Escoamento quanto à
variação no tempo

10. • Rotacional:
• A maioria das partículas desloca-se animada de
velocidade angular em torno de seu centro de massa;
• Irrotacional:
• As partículas se movimentam sem exibir movimento
de rotação (na maioria das aplicações em engenharia
despreza-se a característica rotacional dos
escoamentos)
Classificação do Escoamento quanto ao
movimento de rotação

11. – Uniforme:
Todos os pontos de uma mesma trajetória possuem a
mesma velocidade.
– Variado:
Os pontos de uma mesma trajetória não possuem a
mesma velocidade.
Classificação do Escoamento quanto à
variação da trajetória

12. • Escoamento Laminar:
– As partículas descrevem trajetórias paralelas.
•Escoamento Turbulento:
– As trajetórias são errantes e cuja previsão é impossível;
•Escoamento de Transição:
– Representa a passagem do escoamento laminar para o
turbulento ou vice-versa.
Classificação do Escoamento quanto à
direção da trajetória

13. Experimento de Reynolds
• Consiste na injeção de um corante líquido na posição central
de um escoamento de água interno a um tubo circular de
vidro transparente
• O comportamento do filete do corante ao longo do
escoamento no tubo define três características distintas

14. Experimento de Reynolds
1. Regime Laminar:
– O corante não se mistura com o fluido, permanecendo na
forma de um filete no centro do tubo;
– O escoamento processa-se sem provocar mistura
transversal entre escoamento e o filete, observável de
forma macroscópica;
– Como “não há mistura”, o escoamento aparenta ocorrer
como se lâminas de fluido deslizassem umas sobre as
outras;

15. Experimento de Reynolds
2. Regime de transição:
– O filete apresenta alguma mistura com o fluido, deixando
de ser retilíneo sofrendo ondulações;
– Essa situação ocorre para uma pequena gama de
velocidades e liga o regime laminar a outra forma mais
caótica de escoamento;
– Foi considerado um estágio intermediário entre o regime
laminar e o turbulento;

16. Experimento de Reynolds
3. Regime turbulento:
– O filete apresenta uma mistura transversal intensa, com
dissipação rápida;
– São perceptíveis movimentos aleatórios no interior da
massa fluida que provocam o deslocamento de moléculas
entre as diferentes camadas do fluido (perceptíveis
macroscopicamente);
– Há mistura intensa e movimentação desordenada;

17. Experimento de Reynolds
• Número de Reynolds (Re)
– Para escoamentos em dutos cilíndricos circulares, Reynolds
determinou que há uma relação entre o diâmetro (D), a
velocidade média (V) e a viscosidade cinemática (v)
– O parâmetro estabelecido pela relação entre estas três
grandezas é o NÚMERO DE REYNOLDS (Re):
Re = VD
v

18. Experimento de Reynolds
• Número de Reynolds (Re)
– Re < 2000 - Laminar
– 2000 < Re < 2300 - de Transição
– Re > 2300 - Turbulento

19. • vazão representa a rapidez com a qual um volume escoa.
• As unidades de medida adotadas são geralmente o m³/s,m³/h,
l/h ou o l/s.
• A forma mais simples para se calcular a vazão volumétrica é
apresentada a seguir na equação
19
Vazão

20. • Qv representa a vazão volumétrica,
• V é o volume e
• t o intervalo de tempo para se encher o
reservatório.
20
Vazão

21. • Uma outra forma matemática de se determinar a vazão
volumétrica é através do produto entre a área da seção
transversal do conduto e a velocidade do escoamento neste
conduto como pode ser observado na figura a seguir.
21
Vazão

22. • Pela análise da figura, é possível observar que o volume do
cilindro tracejado é dado por:
• Substituindo essa equação na equação de vazão volumétrica,
pode-se escrever que:
22
Vazão

23. • A partir dos conceitos básicos de cinemática aplicados em
Física, sabe-se que a relação d/t é a velocidade do
escoamento, portanto, pode-se escrever a vazão volumétrica
da seguinte forma:
• Qv representa a vazão volumétrica, v é a velocidade do
escoamento e A é a área da seção transversal da tubulação.
23
Vazão

24. Relações Importantes:
1m³ = 1000litros
1h = 3600s
1min = 60s
Área da seção transversal circular:
24
Vazão

25. Princípio da Conservação da Massa
Equação da Continuidade
• A massa não pode ser criada nem destruída.
• A massa de água que entra em um conduto (forçado ou
livre) é a mesma que sai do conduto, se não houver
contribuição ou retirada do fluido, ao longo do
escoamento.
QA = QB mas: Q = A.v
– Logo:
• A1.v1 = A2.v2
• A1 < A2 v1 > v2
P
Q
A1
A2
v1 v2

26. Equação da energia para um
escoamento permanente de um fluido
incompressível
• Esta equação faz um balanço de energia, por unidade de peso,
entre dois pontos de um escoamento e numa mesma linha de
corrente.
• A energia total num determinado ponto do escoamento
corresponde a:
26

27. • Para encontrarmos, energia por unidade de peso, vamos dividir
por peso que é igual a m.g:
• Onde o termo I, é chamado de carga de pressão,o II de carga
cinética e o III de carga potencial .
27
Equação da energia para um
escoamento permanente de um fluido
incompressível

28. • Fazendo o balanço de energia entre dois pontos 1 e 2 de um
escoamento real , portanto com atrito , temos:
28
Equação da energia para um
escoamento permanente de um fluido
incompressível

29. • Onde ΔH12 indica a perda de energia por atrito, por unidade de
peso que é conhecida como perda de carga.
• Aquilo que é perdido por atrito não mais retorna ao sistema.
Observamos que, ao longo do escoamento, o fluido vai perdendo
energia o que implica que a energia total de um ponto
subsequente é sempre menor do que o anterior e para tornar a
energia total constante é necessário somarmos com a perda de
carga. 29
Equação da energia para um
escoamento permanente de um fluido
incompressível

30. • O diagrama a seguir representa a Equação da Energia.
• PCE: o plano de carga efetiva (P/Υ + v2/2g + z + ΔH12),
• LCE: a linha de carga efetiva (P/Υ + v2/2g + z ) e
• LPE: a linha piezométrica efetiva (P/Υ + z).
30
Equação da energia para um
escoamento permanente de um fluido
incompressível

31. 31

32. • Considerando um escoamento ideal, ou seja sem perdas e
sem equipamentos trocando energia, chegamos à equação de
Bernoulli :
• Todos os termos da Equação da Energia e, por consequência, a
de Bernoulli, têm dimensão de comprimento (L).
32
Equação da energia para um
escoamento permanente de um fluido
incompressível

33. 1. A figura a seguir mostra uma esquema de um reservatório de
grandes dimensões, com a superfície livre mantida em nível
constante, com um duto do qual sai um jato livre de água.
Considerando que não há atrito viscoso e sendo a massa
específica da água, ρ = 1000 Kg/m3, as alturas H = 5 m e h =
2 m e os diâmetros internos D = 4 cm e d = 2 cm ,
determine:
• a vazão do jato livre de água; e
• as pressões relativas nos pontos A e B.
33

34. 34

35. • Os únicos pontos que conhecemos a pressão estão na superfície
livre do reservatório e na saída do tubo. Ambos estão sob a
pressão atmosférica e, como não sabemos a posição do local,
devemos trabalhar na escala efetiva já que em qualquer local a
pressão atmosférica é o referencial, portanto igual a zero.
• Não temos a velocidade do escoamento mas podemos considerar
a velocidade na superfície livre do reservatório nula. Na questão é
informado que o nível do reservatório é mantido constante mas
sempre que nos for dada a informação de um grande
reservatório, via de regra, podemos considerar a velocidade na
superfície livre aproximadamente igual a zero.
35

36. Vamos então indicar na figura os pontos 0
(superfície livre do tanque) e 1(saída de água).
E a equação pode ser simplificada como abaixo, já
que não temos bomba nem turbina conectada ao
escoamento:
36

37. Para a primeira pergunta:
Aplicando a equação da continuidade temos a
vazão,
37

38. Para a segunda pergunta:
Para calcularmos a pressão em A e B, temos que
aplicar a equação de Bernoulli entre os pontos 0 e A
e entre 0 e B, respectivamente .
Vamos inicialmente calcular vA, aplicando a equação
da continuidade e, em seguida substituir na
Equação de Bernoulli. Depois repete-se o
procedimento para calcular PB .
38

39. 39

40. Vamos agora calcular PB
Aplicando Bernoulli de 0 a B:
40

41. 41
Calcular o tempo que levará para encher um
tambor de 214 litros, sabendo-se que a
velocidade de escoamento do líquido é de
0,3m/s e o diâmetro do tubo conectado ao
tambor é igual a 30mm.

42. 42

43. Calcular o diâmetro de uma tubulação, sabendo-se
que pela mesma, escoa água a uma velocidade de
6m/s. A tubulação está conectada a um tanque
com volume de12000 litros e leva 1 hora, 5 minutos
e 49 segundos para enchê-lo totalmente.
43

44. 44
Qual a velocidade da água circulando através de um tubo de 32 mm diâmetro,
quando este reduz seu diâmetro para 25mm, considerando a velocidade da
água no segundo trecho de 4 m/s?
QA = QB
A1.v1 = A2.v2

45. 45
Determine a pressão e velocidade média com a qual a água
escoa nos pontos 1, 2, 3 e 4 no diagrama mostrado a seguir.
Considere fluido perfeito (sem perda de carga). Determine
também a vazão em cada um dos pontos.
Considere o diâmetro igual a 100 mm em toda a tubulação.