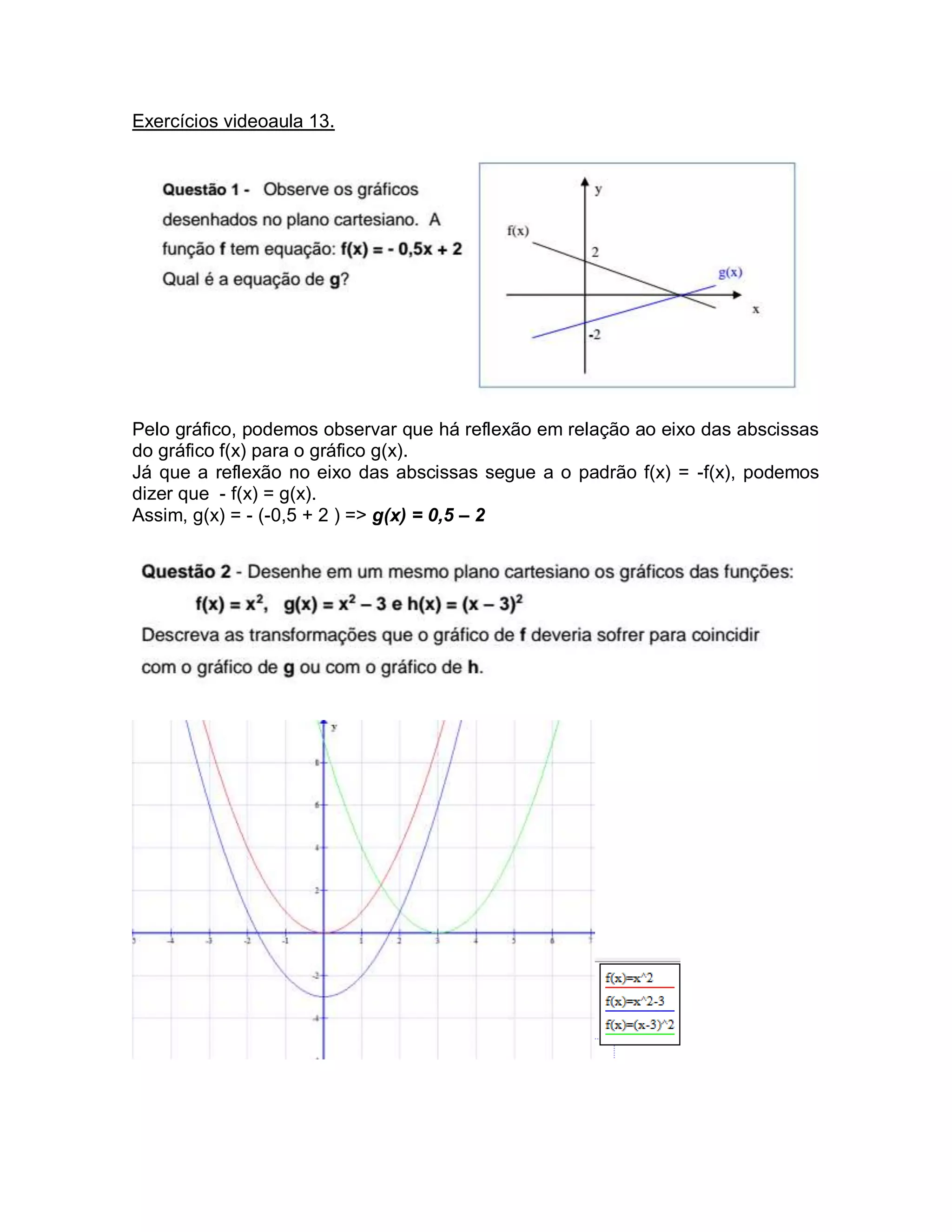
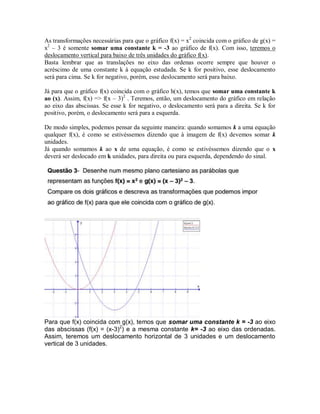
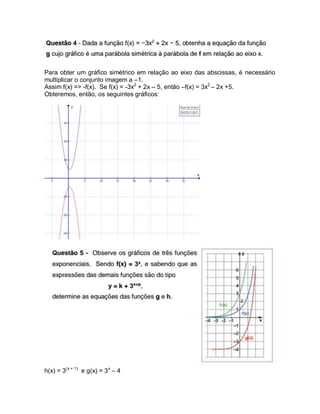
O documento discute transformações de funções gráficas. Explica que a reflexão no eixo das abscissas é representada por f(x) = -f(x) e que a translação vertical é representada por adicionar uma constante à função. Também explica que a translação horizontal ocorre ao adicionar uma constante ao argumento da função.

1. Exercícios videoaula 13.
Pelo gráfico, podemos observar que há reflexão em relação ao eixo das abscissas
do gráfico f(x) para o gráfico g(x).
Já que a reflexão no eixo das abscissas segue a o padrão f(x) = -f(x), podemos
dizer que - f(x) = g(x).
Assim, g(x) = - (-0,5 + 2 ) => g(x) = 0,5 – 2

2. As transformações necessárias para que o gráfico f(x) = x2 coincida com o gráfico de g(x) =
x2 – 3 é somente somar uma constante k = -3 ao gráfico de f(x). Com isso, teremos o
deslocamento vertical para baixo de três unidades do gráfico f(x).
Basta lembrar que as translações no eixo das ordenas ocorre sempre que houver o
acréscimo de uma constante k à equação estudada. Se k for positivo, esse deslocamento
será para cima. Se k for negativo, porém, esse deslocamento será para baixo.
Já para que o gráfico f(x) coincida com o gráfico h(x), temos que somar uma constante k
ao (x). Assim, f(x) => f(x – 3)2 . Teremos, então, um deslocamento do gráfico em relação
ao eixo das abscissas. Se esse k for negativo, o deslocamento será para a direita. Se k for
positivo, porém, o deslocamento será para a esquerda.
De modo simples, podemos pensar da seguinte maneira: quando somamos k a uma equação
qualquer f(x), é como se estivéssemos dizendo que à imagem de f(x) devemos somar k
unidades.
Já quando somamos k ao x de uma equação, é como se estivéssemos dizendo que o x
deverá ser deslocado em k unidades, para direita ou para esquerda, dependendo do sinal.
Para que f(x) coincida com g(x), temos que somar uma constante k = -3 ao eixo
das abscissas (f(x) = (x-3)2) e a mesma constante k= -3 ao eixo das ordenadas.
Assim, teremos um deslocamento horizontal de 3 unidades e um deslocamento
vertical de 3 unidades.

3. Para obter um gráfico simétrico em relação ao eixo das abscissas, é necessário
multiplicar o conjunto imagem a –1.
Assim f(x) => -f(x). Se f(x) = -3x2 + 2x – 5, então –f(x) = 3x2 – 2x +5.
Obteremos, então, os seguintes gráficos:
h(x) = 3(x + 1) e g(x) = 3x – 4