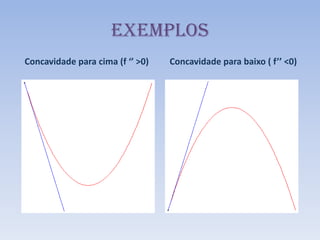
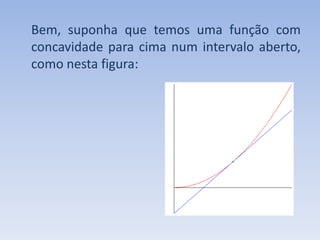
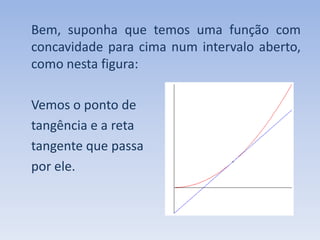
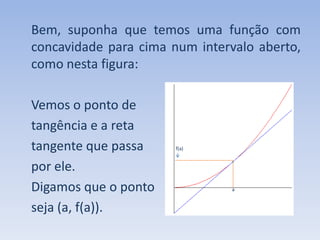
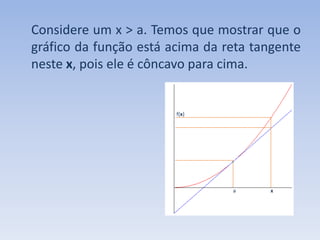
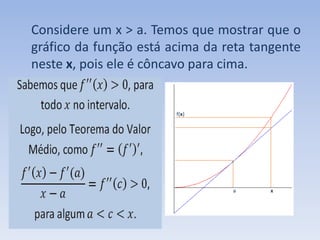
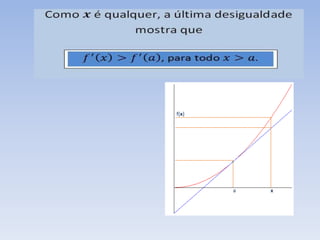
O documento discute como a segunda derivada afeta a concavidade de uma função. Ele explica que quando a segunda derivada é positiva, a função tem concavidade para cima, com o gráfico acima das tangentes. Quando a segunda derivada é negativa, a função tem concavidade para baixo, com o gráfico abaixo das tangentes. O documento ilustra isso geometricamente e analisa como isso ocorre para uma função com concavidade para cima.

1. Teste da concavidadeComo a derivada segunda afeta a concavidade de uma funçãoPor Rogerio Oliveira

2. (a) Num intervalo onde Temos a concavidade para cima, isto é, o gráficode f está acima de todas suas tangentes

3. (a) Num intervalo onde Temos a concavidade para cima, isto é, o gráficode f está acima de todas suas tangentes(b) Num intervalo onde Temos a concavidade para baixo, isto é, o gráfico de f está abaixo de todas suas tangentes

4. ExemplosConcavidade para cima (f ‘’ >0)Concavidade para baixo ( f’’ <0)

5. Mas, como isso acontece?

6. Bem, suponha que temos uma função com concavidade para cima num intervalo aberto, como nesta figura:

7. Bem, suponha que temos uma função com concavidade para cima num intervalo aberto, como nesta figura:

8. Bem, suponha que temos uma função com concavidade para cima num intervalo aberto, como nesta figura:Vemos o ponto detangência e a retatangente que passapor ele.

9. Bem, suponha que temos uma função com concavidade para cima num intervalo aberto, como nesta figura:Vemos o ponto detangência e a retatangente que passaf(a)por ele. Digamos que o ponto aseja (a, f(a)).

10. Considere um x > a. Temos que mostrar que o gráfico da função está acima da reta tangente neste x, pois ele é côncavo para cima. f(x)a x

11. Considere um x > a. Temos que mostrar que o gráfico da função está acima da reta tangente neste x, pois ele é côncavo para cima. f(x)a x

12. f(x)a x