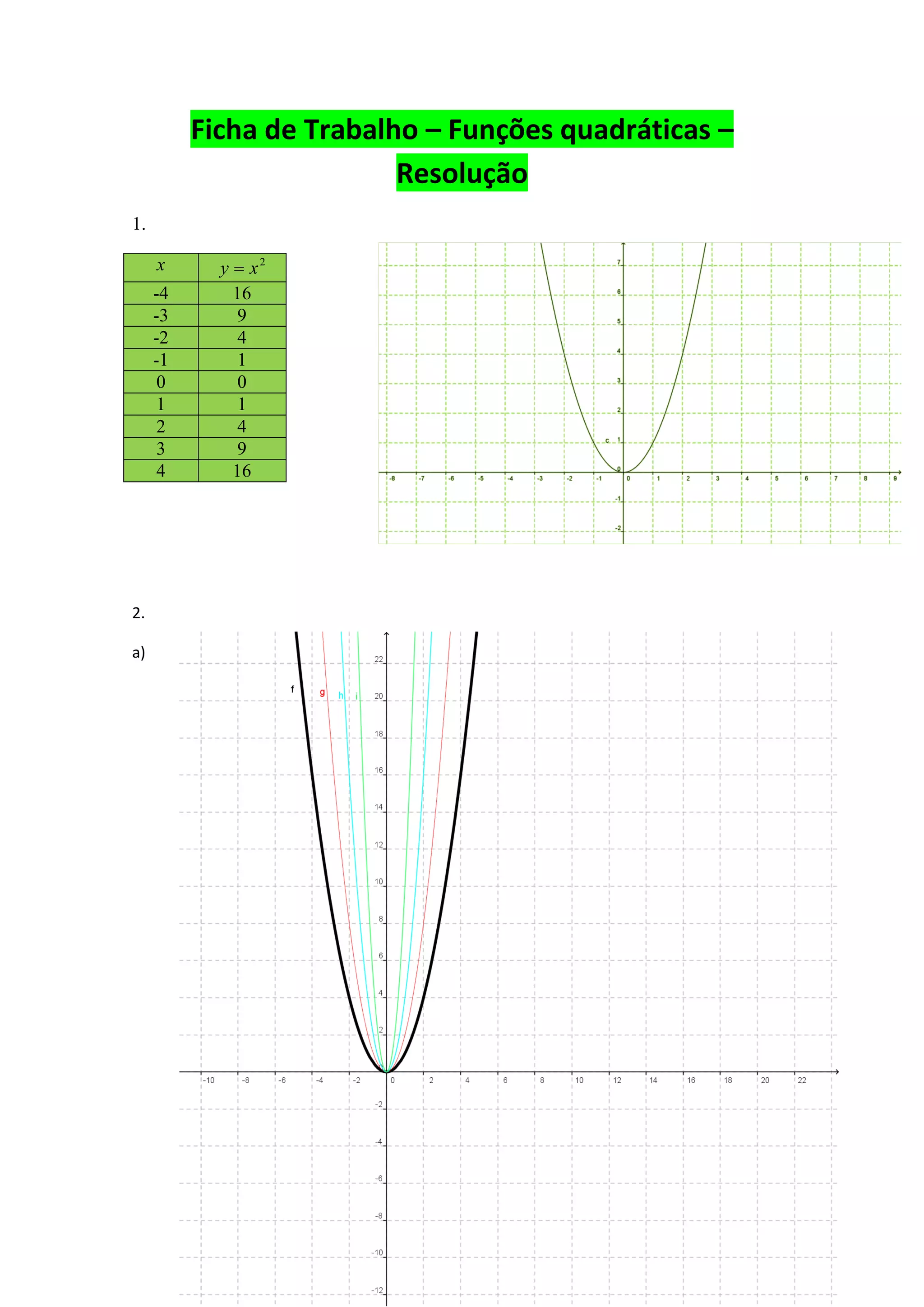
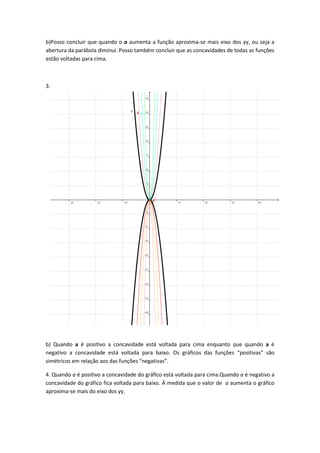
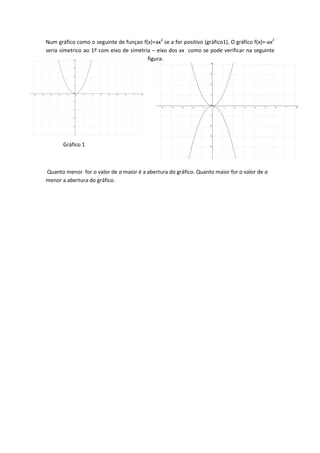
Este documento discute as propriedades das funções quadráticas f(x)=ax2. Ele explica que quando o valor de a é positivo, a concavidade da parábola está voltada para cima e quando a é negativo, está voltada para baixo. Também observa que à medida que o valor absoluto de a aumenta, a parábola se aproxima mais do eixo y e sua abertura diminui.

1. Ficha de Trabalho – Funções quadráticas –
Resolução
1.
x y  x2
-4 16
-3 9
-2 4
-1 1
0 0
1 1
2 4
3 9
4 16
2.
a)

2. b)Posso concluir que quando o a aumenta a função aproxima-se mais eixo dos yy, ou seja a
abertura da parábola diminui. Posso também concluir que as concavidades de todas as funções
estão voltadas para cima.
3.
b) Quando a é positivo a concavidade está voltada para cima enquanto que quando a é
negativo a concavidade está voltada para baixo. Os gráficos das funções “positivas” são
simétricos em relação aos das funções “negativas”.
4. Quando a é positivo a concavidade do gráfico está voltada para cima.Quando a é negativo a
concavidade do gráfico fica voltada para baixo. Á medida que o valor de a aumenta o gráfico
aproxima-se mais do eixo dos yy.

3. Num gráfico como o seguinte de funçao f(x)=ax2 se a for positivo (gráfico1), O gráfico f(x)=-ax2
seria simetrico ao 1º com eixo de simetria – eixo dos xx como se pode verificar na seguinte
figura:
Gráfico 1
Quanto menor for o valor de a maior é a abertura do gráfico. Quanto maior for o valor de a
menor a abertura do gráfico.