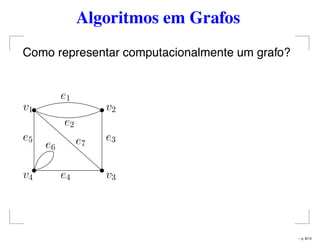
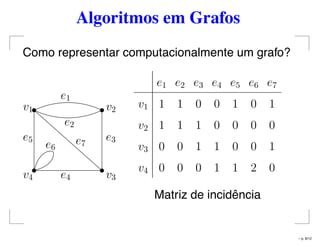
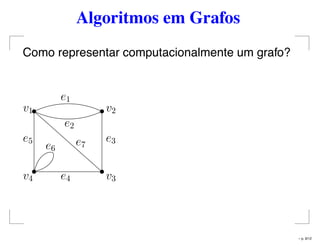
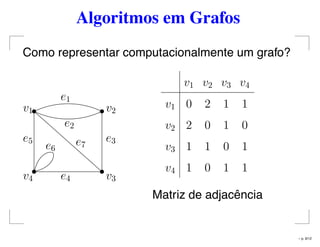
O documento apresenta conceitos básicos sobre grafos, incluindo definição de vértices, arestas, e propriedades como grafo simples, completo e bipartido. Também discute diferentes representações computacionais de grafos, como matrizes de incidência e adjacência. Por fim, destaca algoritmos de busca em grafos, como busca em largura e busca em profundidade.

1. Grafos
Conceitos B´asicos
– p. 1/12

2. Grafos
Um grafo G consiste de um conjunto finito de
elementos chamado v´ertices (denotado por V (G)) e
um conjunto de pares não ordenado de vértices
chamado arestas (denotado por E(G)).
– p. 2/12

3. Grafos
Um grafo G consiste de um conjunto finito de
elementos chamado v´ertices (denotado por V (G)) e
um conjunto de pares não ordenado de vértices
chamado arestas (denotado por E(G)).
Se e é uma aresta e u e v são seus vértices,
dizemos que e liga u a v, e denotamos por e = (u, v)
ou e = uv. Os vértices u e v são os extremos de e.
– p. 2/12

4. Grafos - conceitos básicos
os extremos de uma aresta são incidentes à
aresta, e vice-versa.
– p. 3/12

5. Grafos - conceitos básicos
os extremos de uma aresta são incidentes à
aresta, e vice-versa.
dois vértices incidentes a uma mesma aresta
são adjacentes. O mesmo nome é dado a duas
arestas incidentes a um mesmo vértice.
– p. 3/12

6. Grafos - conceitos básicos
os extremos de uma aresta são incidentes à
aresta, e vice-versa.
dois vértices incidentes a uma mesma aresta
são adjacentes. O mesmo nome é dado a duas
arestas incidentes a um mesmo vértice.
lac¸o: aresta com extremos no mesmo vértice.
– p. 3/12

7. Grafos - conceitos básicos
os extremos de uma aresta são incidentes à
aresta, e vice-versa.
dois vértices incidentes a uma mesma aresta
são adjacentes. O mesmo nome é dado a duas
arestas incidentes a um mesmo vértice.
lac¸o: aresta com extremos no mesmo vértice.
arestas paralelas: ligam os mesmos pares de
vértices.
– p. 3/12

8. Grafos - conceitos básicos
grafo simples: não possui laço nem aresta
paralela.
– p. 4/12

9. Grafos - conceitos básicos
grafo simples: não possui laço nem aresta
paralela.
ordem de um grafo: número de vértices que ele
possui.
– p. 4/12

10. Grafos - conceitos básicos
grafo simples: não possui laço nem aresta
paralela.
ordem de um grafo: número de vértices que ele
possui.
v(G) e a(G): denotam, respectivamente, o
número de vértices e arestas de um grafo G.
Quando o grafo estiver subentendido usaremos
apenas v e a.
– p. 4/12

11. Grafos - conceitos básicos
um grafo é vazio, se não possui vértices.
– p. 5/12

12. Grafos - conceitos básicos
um grafo é vazio, se não possui vértices.
um grafo é completo se cada par de vértices
distintos é ligado por uma aresta. Um grafo
completo com n vértices é denotado por Kn.
– p. 5/12

13. Grafos - conceitos básicos
um grafo é vazio, se não possui vértices.
um grafo é completo se cada par de vértices
distintos é ligado por uma aresta. Um grafo
completo com n vértices é denotado por Kn.
um grafo é conexo se possui uma única
componente.
– p. 5/12

14. Grafos - conceitos básicos
um grafo é bipartido se o seu conjunto de
vértices pode ser particionado em dois
subconjuntos X e Y , tais que cada aresta
possui um extremo em X e outro em Y ; a
partição (X, Y ) é chamada de bipartic¸ ˜ao do
grafo. Um grafo é bipartido completo se ele é
bipartido com bipartição (X, Y ) e todo vértice
de X é ligado a todo vértice de Y . Se |X| = m
e |Y | = n, tal grafo é denotado por Km,n.
– p. 6/12

15. Algoritmos em Grafos
– p. 7/12

16. Algoritmos em Grafos
Como representar computacionalmente um grafo?
– p. 8/12

17. Algoritmos em Grafos
Como representar computacionalmente um grafo?
e1
e2
e3
e4
e5
e6
e7
v1 v2
v3v4
– p. 8/12

18. Algoritmos em Grafos
Como representar computacionalmente um grafo?
e1
e2
e3
e4
e5
e6
e7
v1 v2
v3v4
e1 e2 e3 e4 e5 e6 e7
v1 1 1 0 0 1 0 1
v2 1 1 1 0 0 0 0
v3 0 0 1 1 0 0 1
v4 0 0 0 1 1 2 0
Matriz de incidência
– p. 8/12

19. Algoritmos em Grafos
Como representar computacionalmente um grafo?
– p. 9/12

20. Algoritmos em Grafos
Como representar computacionalmente um grafo?
e1
e2
e3
e4
e5
e6
e7
v1 v2
v3v4
– p. 9/12

21. Algoritmos em Grafos
Como representar computacionalmente um grafo?
e1
e2
e3
e4
e5
e6
e7
v1 v2
v3v4
v1 v2 v3 v4
v1 0 2 1 1
v2 2 0 1 0
v3 1 1 0 1
v4 1 0 1 1
Matriz de adjacência
– p. 9/12

22. Algoritmos de busca em Grafos
Muitas problemas algorítmicos consiste na
exploração de um grafo. Logo, é importante obter
um processo sistemático de como caminhar pelas
arestas e vértices de um grafo.
Vamos descrever dois algoritmos de busca em
grafos:
busca em largura
busca em profundidade
– p. 10/12

23. Busca em largura
O algoritmo de busca em largura para um grafo G
pode ser descrito da seguinte forma:
– p. 11/12

24. Busca em largura
O algoritmo de busca em largura para um grafo G
pode ser descrito da seguinte forma:
põe na fila um vértice qualquer u de G e
marque-o como alcançado
enquanto fila = ∅ faça
v ← elemento da frente da fila (retire v da fila)
para toda aresta (v, w), tal que w ainda não
foi alcançado, marque w como alcançado e
põe w na fila
– p. 11/12

25. Busca em profundidade
O algoritmo de busca em profundidade para um
grafo G pode ser descrito da seguinte forma:
– p. 12/12

26. Busca em profundidade
O algoritmo de busca em profundidade para um
grafo G pode ser descrito da seguinte forma:
empilhe um vértice qualquer u de G e marque-o
como alcançado
enquanto pilha = ∅ faça
v ← elemento do topo-da-pilha
se existe aresta (v, w), tal que w ainda não
foi alcançado, então marque w como
alcançado e empilhe w; senão desempilha v
– p. 12/12