1. O documento descreve a formalização do conceito de limite para funções de uma ou mais variáveis, apresentando as definições formais de limite. 2. Inicialmente, é revisado o conceito intuitivo de limite para funções de uma variável e apresentada a definição formal proposta por Cauchy no século XIX. 3. Em seguida, a definição é generalizada para limite de funções de duas ou mais variáveis, utilizando os conceitos de intervalos em torno do limite e do ponto.

1. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 1
Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite
2.3.1 - Limite de uma fun¸c˜ao de uma vari´avel 2.3.3 - Limite de uma fun¸c˜ao de n vari´aveis
2.3.2 - Limite de uma fun¸c˜ao de duas vari´aveis
Este cap´ıtulo ´e dedicado `a formaliza¸c˜ao do conceito de limite, tanto daquele visto para fun¸c˜oes de uma
vari´avel real quanto para fun¸c˜oes de duas ou mais vari´aveis reais. ´E
um cap´ıtulo de aprofundamento, com
conceitos um pouco mais complexos do que normalmente ´e ensinado em alguns cursos de C´alculo.
2.3.1 - Limite de uma fun¸c˜ao de uma vari´avel
Para definir de forma mais rigorosa o que ´e um limite de fun¸c˜oes de duas ou mais vari´aveis ´e necess´ario
aprofundar o conceito de limite visto at´e ent˜ao. Antes de mostrar a defini¸c˜ao formal do limite de uma fun¸c˜ao
f = f(x) quando x → x0, ´e bom lembrar que, embora o C´alculo Diferencial e Integral tenha surgido com Isaac
Newton (1643-1727) e Gottfried Wilhelm von Leibniz (1646-1717) no s´eculo XVII, foi somente no s´eculo XIX
que essa defini¸c˜ao foi formalizada pelo francˆes Augustin-Louis Cauchy (1789-1857) e pelo alem˜ao Karl Theodor
Wilhelm Weierstrass (1815-1897).
Dado um limite lim
x!x0
f(x) = L, a defini¸c˜ao formal baseia-se em construir dois intervalos abertos: um em
torno do limite L e outro em torno do ponto x0, como mostra a primeira figura a seguir. O intervalo em torno
de x0 tem que ser pequeno o suficiente para que a sua imagem esteja contida no intervalo em torno do limite
L (segunda figura a seguir).
x
y
x0
L
bc
bc
y
bc
bcbc x
x0
L
bc
bcbc
Prova-se que o limite ´e verdadeiro se, para qualquer intervalo em torno de L, n˜ao importa o qu˜ao pequeno
ele seja, for sempre poss´ıvel encontrar um intervalo em torno de x0 de modo que a imagem desse intervalo esteja
contida no intervalo em torno de L. A figura a seguir mostra um caso em que isto n˜ao ´e poss´ıvel, mostrando
que o limite ´e falso.
bc
Lb
bc
bc
bcbc x
x
g(x)
bc
Lb
bc
bc
0 x0
g(x)
bcbc
0 x0
Determinando que o intervalo em torno de L ´e dado por (L − ǫ,L + ǫ) e o intervalo em torno de x0 ´e dado
por (x0 − δ, x0 + δ), onde ǫ (´epsilon) e δ (delta) s˜ao ambos maiores que zero, podemos dizer que o limite est´a

2. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 2
correto se, para y ∈ (L−ǫ,L+ǫ), existir sempre um δ > 0 tal que x ∈ (x0−δ, x0 +δ). Isto tem que ser verdade
para qualquer valor de ǫ que escolhermos. Um exemplo mais espec´ıfico ´e dado a seguir.
Isaac Newton (1642-1727): Newton foi um dos maiores gˆenios da humanidade. Nasceu na pequena cidade
de Woolsthorpe, na Inglaterra, e estudou na Universidade de Cambridge, tornando-se depois professor nessa
mesma universidade. Ele era f´ısico, matem´atico, astrˆonomo e alquimista, tendo contribu´ıdo significativamente
para todos esses campos. Ele foi o criador da mecˆanica racional e da lei da gravita¸c˜ao universal. Foi um dos
criadores do C´alculo Diferencial e Integral, juntamente com Leibniz. Desenvolveu v´arios trabalhos em ´optica,
tendo revolucionado essa ´area da F´ısica. Tamb´em foi dele a inven¸c˜ao do telesc´opio refletor, que ´e usado em
observat´orios do mundo inteiro e no espa¸co. Newton tamb´em exerceu importantes cargos p´ublicos e foi sagrado sir
(cavalheiro) pela rainha da Inglaterra na ´epoca. Morreu como uma celebridade em seu pa´ıs, embora j´a mostrasse
v´arios sinais de demˆencia senil.
Gottfried Wilhelm von Leibniz (1646-1717): matem´atico, fil´osofo, f´ısico e estudioso das leis alem˜ao. Nasceu
em Leipzig e estudou na prestigiosa universidade de mesmo nome. Junto com Newton, foi o criador do C´alculo
Diferencial e Integral. Tamb´em foi respons´avel por boa parte da nota¸c˜ao matem´atica usada at´e hoje. Al´em disso,
foi um grande fil´osofo, tendo tecido uma vis˜ao de um universo baseado em princ´ıpios fundamentais e racionais, sem
rejeitar as concep¸c˜oes crist˜as. Sua convic¸c˜ao de que tudo podia ser demonstrado racionalmente quando utilizada
uma nota¸c˜ao coveniente levou-o a organizar v´arias express˜oes matem´aticas em termos de s´ımbolos. Leibniz sofreu
revezes com a rivalidade entre ele e Newton devida `a controv´ersia sobre quem teria sido o criador do C´alculo
Diferencial e Integral.
Exemplo 1: tentaremos mostrar que limx → 1x2 = 1 usando o novo crit´erio que acaba de ser descrito. Tomando
um
intervalo que inclui todos os n´umeros que est˜ao a distˆancias menores que ǫ = 1 do ponto y = 1, temos que esse intervalo
vai de y = 0 at´e y = 2. Este intervalo tem comprimento 2ǫ = 2 e pode ser escrito como (0, 2). Se considerarmos
agora um intervalo centrado em x = 1 de comprimento 2δ = 0, 4, isto ´e, o intervalo (1 − 0, 2 , 1 + 0, 2) = (0, 8 , 1, 2),
este produzir´a a seguinte imagem em y: para x = 0, 8 temos f(0, 8) = 0, 64; para x = 1, 2, f(1, 4) = 1, 44. Portanto,
a imagem produzida pelo intervalo em x centrado em x = 1 e de comprimento 2δ = 0, 4 produz uma imagem em y
dada pelo intervalo (0, 64 , 1, 44), que est´a contido no intervalo (0, 2).
x
y
−2 −1 0
1 2
4
3
2
1
bc
bc
2ǫ = 2
x
y
−2 −1 0
1 2
4
3
2
1
bc
bc
bcbc
2ǫ = 2
2δ = 0, 4
Do mesmo modo como escolhemos 2δ = 0, 4 ⇒ δ = 0, 2, poder´ıamos ter escolhido δ = 0, 1 ou δ = 0, 4, que a
imagem produzida pelo intervalo (1−δ, 1+δ) ainda estaria contida no intervalo (0, 2). Na verdade, contanto que δ
seja menor ou igual a √2 − 1 ≈ 0, 414, o intervalo produzido em x leva a uma imagem que est´a contida em (0, 2).
Vamos mostar que tamb´em para valores menores de ǫ conseguimos encontrar valores de δ satisfazendo essas
condi¸c˜oes. Escolhendo ǫ = 0, 5, temos o intervalo (1 − 0, 5 , 1 + 0, 5) = (0, 5 , 1, 5) em y. O que temos que fazer
agora ´e encontrar um valor de δ para o qual o intervalo (1−δ, 1+δ) em x produza uma imagem que esteja contida
no intervalo em y. Tomando δ = 0, 2, teremos o intervalo (1 − 0, 2 , 1 + 0, 2) = (0, 8 , 1, 2) em x que, como j´a
vimos, produz a imagem (0, 64 , 1, 44), que est´a contida no intervalo (0, 5 , 1, 5).

3. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 3
x
y
−2 −1 0
1 2
4
3
2
1
bc
bc
2ǫ = 1
x
y
−2 −1 0
1 2
4
3
2
1
bc
bc
bcbc
2ǫ = 1
2δ = 0, 4
Tomemos agora um valor ainda menor para ǫ: 0,25. Para este valor, temos o intervalo (1 − 0, 25 , 1 + 0, 25) =
= (0, 75 , 1, 25) em y. Escolhendo δ = 0, 1, temos o intervalo (1−0, 1 , 1+0, 1) = (0, 9 , 1, 1) em x, que tem como
imagem o intervalo (0, 81 , 1, 21), que est´a contido no intervalo (0, 75 , 1, 25).
x
y
−2 −1 0
1 2
4
3
2
1
bc
bc
2ǫ = 0, 5
x
y
−2 −1 0
1 2
4
3
2
1
bc
bc
bcbc
2ǫ = 0, 5
2δ = 0, 2
Assim, podemos intuir que, para qualquer valor de ǫ que escolhermos, ser´a sempre poss´ıvel escolher um valor de
δ tal que o intervalo (1 − δ, 1 + δ) em x produzir´a uma imagem em y que estar´a contida no intervalo (1 − ǫ, 1 + ǫ).
Diremos que o limite existe e est´a correto quando isto puder ser provado.
Voltemos, agora, `a defini¸c˜ao formal de um limite. Podemos dizer que o limite de uma fun¸c˜ao f(x) quando
x tende a x0 ´e L, lim
x!x0
f(x) = L se, para qualquer ǫ > 0, existir sempre um δ > 0 tal que x ∈ (x0 −δ, x0 +δ) ⇒
⇒ f(x) ∈ (L − ǫ,L + ǫ).
Agora, podemos escrever |x − x0| < δ no lugar de x ∈ (x0 − δ, x0 + δ). Isto porque
|x − x0| < δ ⇔ −δ < x − x0 < δ ⇔ x0 − δ < x < x0 + δ .
De modo semelhante, podemos escrever |f(x) − L| < ǫ no lugar de f(x) ∈ (L − ǫ,L + ǫ). Isto porque
|f(x) − L| < ǫ ⇔ −ǫ < f(x) − L < ǫ ⇔ L − ǫ < f(x) < L + ǫ .
Portanto, a defini¸c˜ao de limite fica dada a seguir. lim
x!x0
f(x) = L se, para qualquer ǫ > 0, existir sempre um
δ > 0 tal que |x − x0| < δ ⇒ |f(x) − L| < ǫ.
Defini¸c˜ao 1 - Dada uma fun¸c˜ao f(x) definida em um intervalo I ⊂ R e um ponto x0 de I, dizemos que
o limite de f(x) quando x tende a x0 existe e ´e igual a L, o que pode ser escrito como lim
x!x0
f(x) = L,
quando, para qualquer ǫ > 0, existir sempre um δ > 0 tal que |x − x0| < δ ⇒ |f(x) − L| < ǫ.

4. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 4
Observa¸c˜ao: uma defini¸c˜ao mais formal de limite ´e feita na Leitura Complementar 2.3.3 e necessita do conceito
de ponto de acumula¸c˜ao, que ´e visto na Leitura Complementar 2.3.2.
A defini¸c˜ao 2 ´e usada a seguir para provar dois limites.
Exemplo 2: mostre que lim
(x + 2) = 5.
x!3
Solu¸c˜ao: temos que mostrar que existem valores de δ > 0 tais que |x−a| < δ ⇒ |f(x)−L| < ǫ para qualquer valor
de ǫ > 0. Temos a = 3, f(x) = x + 2 e L = 5, de modo que a express˜ao fica
|x − 3| < δ ⇒ |x + 2 − 5| < ǫ ⇔ |x − 3| < δ ⇒ |x − 3| < ǫ ⇔ .
Podemos ver da express˜ao acima que sempre que tivermos δ ≤ ǫ, essa rela¸c˜ao ser´a v´alida, pois se |x − 3| < δ e
δ ≤ ǫ, ent˜ao |x − 3| < ǫ. Portanto, o limite est´a provado.
Exemplo 3: mostre que lim
(2x − 1) = 1.
x!1
Soluc¸ao: ˜temos que mostrar que existem valores de δ > 0 tais que |x−a| < δ ⇒ |f(x)−L| < ǫ para qualquer valor
de ǫ > 0. Temos a = 1, f(x) = 2x − 1 e L = 1, de modo que a express˜ao fica
ǫ
|x−1| < δ ⇒ |2x−1−1| < ǫ ⇔ |x−1| < δ ⇒ |2x−2| < ǫ ⇔ |x−1| < δ ⇒ 2|x−1| < ǫ ⇔ |x−1| < δ ⇒ |x−1| <
.
2
Podemos ver da express˜ao acima que sempre que tivermos δ ≤ ǫ
2 , essa rela¸c˜ao ser´a v´alida, pois se |x − 1| < δ e
δ ≤ ǫ
2 , ent˜ao |x − 1| < ǫ. Portanto, o limite est´a provado.
A defini¸c˜ao de limites que acabamos de desenvolver n˜ao ´e v´alida para limites infinitos ou limites envolvendo
o infinito. Para esses limites e outros s˜ao necess´arias novas defini¸c˜oes. Na verdade, s˜ao necess´arias nove delas
(isto ´e feito na Leitura Complementar 2.3.3).
Augustin-Louis Cauchy (1789-1857): matem´atico francˆes respons´avel pela formula¸c˜ao mais precisa do conceito
de limites e por v´arias contribui¸c˜oes de fundamental importˆancia na teoria de fun¸c˜oes de vari´aveis complexas e
em equa¸c˜oes diferenciais. Cauchy teve uma infˆancia atribulada, tendo vivido na ´epoca da Revolu¸c˜ao Francesa.
Trabalhou como engenheiro para a marinha de Napole˜ao e teve v´arias tentativas de obter posi¸c˜oes em universidades
recusadas, muitas vezes por motivos pol´ıticos. Cat´olico devoto, teve atritos com seus colegas partid´arios do ate´ısmo.
Quando o rei da Fran¸ca voltou ao poder, recusou-se a jurar lealdade e perdeu seu emprego, retornando ao seu
trabalho ap´os o rei ter sido novamente deposto.
Karl Theodor Wilhelm Weierstrass (1789-1857): matem´atico nascido na Pr´ussia (atual Alemanha). Embora
fosse apaixonado pela matem´atica, estudou finan¸cas por desejo de seu pai. Desinteressado do assunto, levou uma
vida despreocupada de estudante at´e que resolveu, contrariando seu pai, estudar matem´atica. Tendo abandonado
a universidde, formou-se professor do segundo grau. Exerceu essa profiss˜ao at´e publicar um artigo sobre invers˜ao
de fun¸c˜oes hiperel´ıpticas, o que lhe valeu uma posi¸c˜ao na universidade. ´E
considerado o pai da an´alise matem´atica
por ter introduzido o rigor atual no C´alculo e na teoria de fun¸c˜oes de vari´aveis complexas. Fez muitas contribui¸c˜oes
`a matem´atica, sobretudo nesses dois ´ultimos campos. Suas aulas eram muito apreciadas e ele tinha estudantes
vindos de v´arias partes do mundo.
2.3.2 - Limite de uma fun¸c˜ao de duas vari´aveis
Podemos, agora, expandir o conceito de limite para o caso de uma fun¸c˜ao de duas vari´aveis reais. Relem-brando,
uma fun¸c˜ao f = f(x, y) leva elementos de R2 a elementos de R (primeira figura a seguir).

5. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 5
b
x
y
x0
y0
z
f(x0, y0)
f
R2 R
Para definirmos um limite lim
(x0,y0)
f(x, y) = L, precisamo primeiro determinar uma regi˜ao em torno do ponto
(x0, y0) e um outro intervalo aberto em torno do limite L. Podemos, por exemplo, desenhar um quadrado
ou uma circunferˆencia em torno de (x0, y0) (duas figuras a seguir) e dizer que (x, y) tem que estar dentro do
subconjunto de R2 constitu´ıdo pela regi˜ao interna a esse quadrado ou a essa circunferˆencia, excluindo as suas
bordas (isto ´e representado pelas linhas pontilhadas nas figuras a seguir).
b
x
y
x0
y0
z
L
f
bc
bc
b
x
y
x0
y0
z
L
f
bc
bc
Como ´e mais f´acil determinar a equa¸c˜ao da regi˜ao circular em torno do ponto (x0, y0), escolheremos esse
tipo de regi˜ao, que chamaremos de bola aberta em torno do ponto, pois ela n˜ao inclui a superf´ıcie do c´ırculo.
Podemos, ent˜ao, dizer que a regi˜ao limitada pela bola aberta ´e dada pelo c´ırculo
(x − x0)2 + (y − y0)2 < δ2 = p(x − x0)2 + (y − y0)2 < δ ,
onde δ ´e o raio da bola aberta.
Lembrando agora que p(x − x0)2 + (y − y0)2 = ||(x − x0, y − y0)||, podemos dizer que a bola aberta ´e
definida por ||(x − x0, y − y0)|| < δ. Podemos, ent˜ao, utilizar a seguinte defini¸c˜ao de limite.
Defini¸c˜ao 2 - Dada uma fun¸c˜ao f(x, y) definida em um intervalo I ⊂ R2 e um ponto (x0, y0) ∈ I,
dizemos que o limite de f(x, y) quando (x, y) tende a (x0, y0) existe e ´e igual a L, o que pode ser
escrito como lim
(x,y)!(x0,y0)
f(x, y) = L, quando, para qualquer ǫ > 0, existir sempre um δ > 0 tal que
||x − x0, y − y0|| < δ ⇒ |f(x, y) − L| < ǫ.
Vamos usar esta defini¸c˜ao para provar um limite bem simples, a seguir.
Exemplo 1: prove que lim
(x,y)!(x0,y0)
x = x0.
Solu¸c˜ao: temos que mostrar que, para qualquer ǫ > 0, existe um δ > 0 tal que
||x − x0, y − y0|| < δ ⇒ |f(x, y) − L| < ǫ ⇔ p(x − x0)2 + (y − y0)2 < δ ⇒ |x − x0| < ǫ .
Sabemos que p(x − x0)2 ≤ p(x − x0)2 + (y − y0)2 ⇔ |x−x0| ≤ p(x − x0)2 + (y − y0)2. Portanto, escolhendo
qualquer δ ≤ ǫ, temos que p(x − x0)2 + (y − y0)2 < δ ⇒ |x − x0| < ǫ, o que prova o limite.
Em geral, ´e muito dif´ıcil provar limites envolvendo fun¸c˜oes de duas vari´aveis. Podemos, no entanto, calcular
alguns limites utilizando nossos conhecimentos de limites de fun¸c˜oes de uma vari´avel, como mostra o exemplo
a seguir.

6. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 6
Exemplo 2: calcule lim
(x,y)!(0,0)
sen (x2 + y2)
x2 + y2 .
Solu¸c˜ao: usando a simetria do problema, podemos fazer a mudan¸ca de vari´avel x2+y2 = r2. Quando (x, y) → (0, 0),
teremos r → 0, tamb´em, de modo que podemos escrever
lim
(x,y)!(0,0)
sen (x2 + y2)
x2 + y2 = lim
r!0
sen r2
r2 .
Se aplicarmos r = 0, este limite fica da forma 0
0 , de modo que podemos aplicar a ele a regra de L’Hˆopital:
lim
(x,y)!(0,0)
sen (x2 + y2)
x2 + y2 = lim
r!0
sen r2
r2 = lim
r!0
2r cos r2
2r
= lim
r!0
cos r2 = cos 0 = 1 .
Vamos, agora, provar que um limite n˜ao existe.
Exemplo 3: calcule lim
(x,y)!(0,0)
x2 − y2
x2 + y2 .
Solu¸c˜ao: o procedimento que adotaremos ´e fazer o limite de uma das vari´aveis e depois o limite da outra. Come¸cando
pelo limite x → 0, temos
lim
(x,y)!(0,0)
x2 − y2
x2 + y2 = lim
y!0
−y2
y2 = lim
(−1) = −1 .
y!0
Se fizermos primeiro o limite em y e depois o limite em x, obtemos
lim
(x,y)!(0,0)
sen (x2 + y2)
x2 + y2 = lim
x!0
x2
x2 = lim
x!0
1 = 1 .
Note que os dois limites n˜ao s˜ao iguais. Isto j´a basta para provar que n˜ao existe esse limite.
Na verdade, os exemplos 2 e 3 n˜ao est˜ao formalizados da maneira correta. A Leitura Complementar 2.3.4
mostra como fazˆe-lo.
2.3.3 - Limite de uma fun¸c˜ao de n vari´aveis
Vamos, agora, definir limites para o caso de uma fun¸c˜ao de trˆes vari´aveis reais. A generaliza¸c˜ao para fun¸c˜oes
de n vari´aveis reais poder´a ser feita facilmente a partir da´ı. Uma fun¸c˜ao f = f(x, y, z) leva elementos de R3 a
elementos de R (figura a seguir). Podemos considerar uma bola aberta em trono de R3 dada por uma esfera
de raio menor que δ levando a um interavalo |f(x, y, z) − L| < ǫ na imagem (segunda figura a seguir).
b
z
z0
x0 y0
x y
w
f(x0, y0, z0)
f
R3 R
b
z
z0
x0 y0
x y
w
L
f
bc
bc
R3 R
Podemos escrever a regi˜ao dentro dessa bola aberta pela equa¸c˜ao p(x − x0)2 + (y − y0)2 + (z − z0)2 < δ,
que ´e a equa¸c˜ao de uma esfera de raio δ com exce¸c˜ao de sua superf´ıcie. Novamente, podemos trocar a raiz por
uma norma: ||(x − x0, y − y0, z − z0)|| < δ. A defini¸c˜ao de limite fica, ent˜ao, como a dada a seguir.

7. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 7
Defini¸c˜ao 3 - Dada uma fun¸c˜ao f(x, y, z) definida em um intervalo I ⊂ R3 e um ponto (x0, y0, z0) ∈ I,
dizemos que o limite de f(x, y, z) quando (x, y, z) tende a (x0, y0, z0) existe e ´e igual a L, o que pode
ser escrito como lim
(x,y,z)!(x0,y0,z0)
f(x, y, z) = L, quando, para qualquer ǫ > 0, existir sempre um δ > 0
tal que ||(x − x0, y − y0, z − z0)|| < δ ⇒ |f(x, y, z) − L| < ǫ.
A generaliza¸c˜ao para o limite de uma fun¸c˜ao de n vari´aveis reais ´e direta.
Defini¸c˜ao 4 - Dada uma fun¸c˜ao f(x1, · · · , xn) definida em um intervalo I ⊂ Rn e um ponto
(x10, · · · , xn0) ∈ I, dizemos que o limite de f(x1, · · · , xn) quando (x1, · · · , xn) tende a (x01, · · · , x0n) ex-iste
e ´e igual a L, o que pode ser escrito como lim
(x1,··· ,xn)!(x10,··· ,xn0)
f(x1, · · · , xn) = L, quando, para qual-quer
ǫ > 0, existir sempre um δ > 0 tal que ||(x1−x10, · · · , xn−xn0)|| < δ ⇒ ⇒ |f(x1, · · · , xn)−L| < ǫ.
Resumo
• Limite de uma fun¸c˜ao f : R → R. Dada uma fun¸c˜ao f(x) definida em um intervalo I ⊂ R
e um ponto x0 de I, dizemos que o limite de f(x) quando x tende a x0 existe e ´e igual a L, o que
pode ser escrito como lim
x!x0
f(x) = L, quando, para qualquer ǫ > 0, existir sempre um δ > 0 tal que
|x − x0| < δ ⇒ |f(x) − L| < ǫ.
• Limite de uma fun¸c˜ao f : R2 → R. Dada uma fun¸c˜ao f(x, y) definida em um intervalo I ⊂ R2 e
um ponto (x0, y0) ∈ I, dizemos que o limite de f(x, y) quando (x, y) tende a (x0, y0) existe e ´e igual
a L, o que pode ser escrito como lim
(x,y)!(x0,y0)
f(x, y) = L, quando, para qualquer ǫ > 0, existir sempre
um δ > 0 tal que ||x − x0, y − y0|| < δ ⇒ |f(x, y) − L| < ǫ.
• Limite de uma fun¸c˜ao f : R3 → R. Dada uma fun¸c˜ao f(x, y, z) definida em um intervalo I ⊂ R3
e um ponto (x0, y0, z0) ∈ I, dizemos que o limite de f(x, y, z) quando (x, y, z) tende a (x0, y0, z0) existe
e ´e igual a L, o que pode ser escrito como lim
(x,y,z)!(x0,y0,z0)
f(x, y, z) = L, quando, para qualquer ǫ > 0,
existir sempre um δ > 0 tal que ||(x − x0, y − y0, z − z0)|| < δ ⇒ |f(x, y, z) − L| < ǫ.
• Limite de uma func¸˜ao f : Rn → R. Dada uma func¸ao ˜f(x1, · · · , xn) definida em um intervalo
I ⊂ Rn e um ponto (x10, · · · , xn0) ∈ I, dizemos que o limite de f(x1, · · · , xn) quando (x1, · · · , xn) tende
a (x01, · · · , x0n) existe e ´e igual a L, o que pode ser escrito como lim
f(x1, · · · , xn) = L,
(x1,··· ,x)!(x10,··· ,xn0)
nquando, para qualquer ǫ > 0, existir sempre um δ > 0 tal que ||(x1 − x10, · · · , xn − xn0)|| < δ ⇒
⇒ |f(x1, · · · , xn) − L| < ǫ.

8. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 8
Leitura Complementar 2.3.1 - Desigualdades
e m´odulo
Os s´ımblos < (menor), > (maior), ≤ (menor ou igual) e ≥ (maior ou igual) estabelecem rela¸c˜oes de ordem
no conjunto dos n´umeros reais. Isto tamb´em vale para os subconjuntos N, Z e Q. Uma rela¸c˜ao de ordem entre
dois n´umeros reais tamb´em ´e chamada de desigualdade.
2 ≥ √2 .
Exemplos: 2 < 7 , −4 > −8 , 3, 4 ≤ 5 , 3
Existem certas regras quando se opera com desigualdades. Para quaisquer n´umeros reais a e b, valem as
seguintes propriedades:
P1) a < b ⇔ a + c < b + c , c ∈ R;
P2) a < b e c < d ⇔ a + c < b + d , c ∈ R e d ∈ R;
P3) a < b ⇔ ac < bc , c ∈ R e c > 0;
P4) a < b ⇔ ac > bc , c ∈ R e c < 0;
P5) a < b ⇔ 1
a > 1
b , a6= 0 e b6= 0.
Exemplos dessas regras s˜ao dados a seguir.
Exemplo 1: 2 < 3 ⇔ 2 + 4 < 3 + 4 ⇔ 6 < 7 (por P1).
Exemplo 2: 1 < 4 ⇔ 1 + 3 < 4 + 6 ⇔ 4 < 10 (por P2).
Exemplo 3: 2 < 3 ⇔ 2 · 3 < 3 · 3 ⇔ 6 < 9 (por P3).
Exemplo 4: 2 < 3 ⇔ 2 · (−1) < 3 · (−1) ⇔ −2 > −3 (por P4).
Exemplo 5: 2 < 4 ⇔ 1
2 > 1
4 (por P5).
a) M´odulo de um n´umero real
O m´odulo ou valor absoluto de um n´umero real a, escrito |a|, ´e definido como
|a| = a se a ≥ 0 ; |a| = −a se a < 0 .
Outra defini¸c˜ao ´e dada em termos da raiz quadrada de um n´umero ao quadrado:
|a| = √a2 .
Exemplos: |2| = 2 , | − 4| = 4 , | − 3| = p(−3)2 = √9 = 3 .
O m´odulo de um n´umero representa a distˆancia deste ao ponto 0 no eixo dos n´umeros reais.

9. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 9
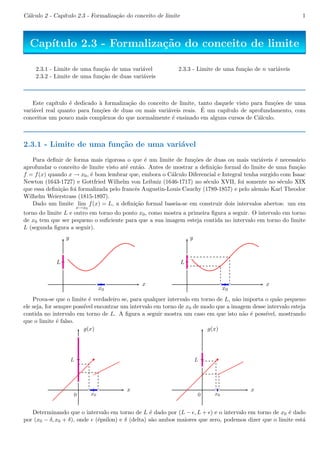
0 a
|a|
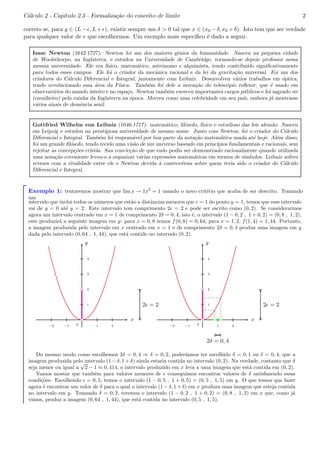
b 0
|b|
Usamos esta interpreta¸c˜ao para estabelecer algumas rela¸c˜oes para um n´umero x ∈ R com rela¸c˜ao a um
n´umero a > 0. Primeiro,
|x| = a ⇔ x = ±a .
Exemplo 1: calcule x quando |x| = 2.
Solu¸c˜ao: |x| = 2 ⇔ x = ±2, ou seja, x = 2 ou x = −2.
A segunda rela¸c˜ao ´e a seguinte:
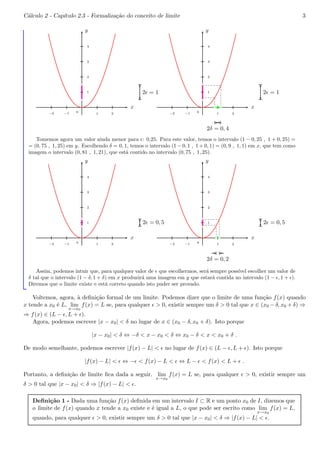
|x| < a ⇔ −a < x < a .
Isto pode ser visto da figura abaixo. O m´odulo de x ser´a menor que a quando x estiver dentro do intervalo
aberto (−a, a) (outra nota¸c˜ao usada para o intervalo aberto ´e ] − a, a[ ).
x
−a 0 a
bcbc
|x|
Exemplo 2: calcule x quando |x| < 4.
Solu¸c˜ao: |x| < 2 ⇔ −2 < x < 2, ou seja, x ∈ (−2, 2).
A terceira rela¸c˜ao ´e:
|x| > a ⇔ x < −a ou x > a .
Isto pode ser visto da figura abaixo. O m´odulo de x ser´a maior que a quando x estiver dentro do intervalo
aberto (−∞, a) ou no intervalo aberto (a,∞).
−a 0 a
bcbc
x
|x|
−a 0 a
bcbc
x
|x|
Exemplo 3: calcule x quando |x| > 3.
Solu¸c˜ao: |x| > 3 ⇔ x < −3 ou x > 3, ou seja, x ∈ (−∞,−3) ∪ (3,∞).
De modo semelhante, podemos escrever
|x| ≤ a ⇔ −a ≤ x ≤ a , |x| ≥ a ⇔ x ≤ −a ou x ≥ a .
Exemplo 4: calcule x quando |x| ≤ 3.
Solu¸c˜ao: |x| ≤ 3 ⇔ −3 ≤ x ≤ 3, ou seja, x ∈ [−3, 3].
O m´odulo de um n´umero real apresenta as seguintes propriedades:

11. P1) |

13. ab| = |a| · |b|;
P2) a
= |a|
b|b| , b6= 0;
P3) |a + b| ≤ |a| + |b| (desiguladade triangular).

14. C´alculo 2 - Cap´ıtulo 2.3 - Formaliza¸c˜ao do conceito de limite 10
Demonstra¸c˜ao:
P1) podemos escrever |ab| = p(ab)2 = √a2b2 = √a2√b2 = |a| · |b|.
P2) temos

16. a
b

18. = qa
b 2
= qa2
b2 =
pa2
pb2 = |a|
|b|
.
P3) dados dois n´umeros reais, sabemos que −|a| ≤ a ≤ |a| e −|b| ≤ b ≤ |b|. Portanto, temos
−|a| − |b| ≤ a + b ≤ |a| + |b| ⇔ −(|a| + |b|) ≤ a + b ≤ |a| + |b| ⇔ |a + b| |a| + |b| .
Exemplo 5: |3 · (−2)| = | − 6| = 6 = |3| · |2|.
Exemplo 6:

20. −1
2