Aula 17 geometria básica

CURSO ONLINE – RACIOCÍNIO LÓGICO 1

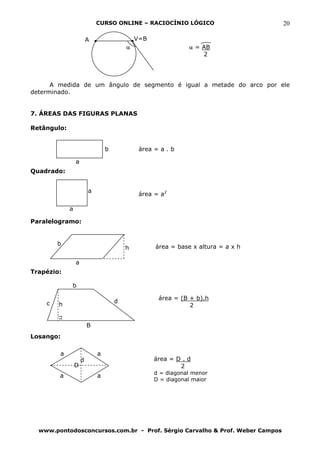
AULA DEZESSETE: GEOMETRIA BÁSICA
Olá, amigos!
Novamente pedimos desculpas por não ter sido possível apresentarmos esta aula 17 na
semana passada.
Daremos hoje início a um novo assunto: GEOMETRIA!
Como de praxe, apresentaremos muitas questões de concursos passados que servirão
no nosso aprendizado, e também para sabermos qual é a profundidade exigida deste assunto
dentro das provas de Raciocínio Lógico.
Apresentaremos a seguir, a solução do dever de casa da aula passada, sobre o assunto
de Trigonometria. Vamos a elas!

DEVER DE CASA

01.(AFC-STN-2000 ESAF) A expressão dada por y = 3senx + 4 é definida para todo
número x real. Assim, o intervalo de variação de y é
a) -1 ≤ y ≤ 7
b) -7 < y < 1
c) -7 < y ≤ -1
d) 1 ≤ y < 7
e) 1 ≤ y ≤ 7

Sol.:
A expressão fornecida no enunciado envolve a função seno. Assim, encontraremos o
intervalo de variação de y, a partir do intervalo de variação da função seno.
Da função seno, sabemos que o seu intervalo de variação é: [-1, 1], ou seja, o valor
máximo é 1, e o valor mínimo é -1. E podemos escrever que:
sen x ≥ -1 e sen x ≤ 1

A partir da expressão sen x ≥ -1, obteremos uma expressão de variação de y.

Temos que sen x ≥ -1 , se multiplicarmos por 3 ambos os lados, obteremos:
3.sen x ≥ 3.(-1)
Daí:
3sen x ≥ -3

Se somarmos 4 a ambos os lados da expressão acima, teremos:
3sen x + 4 ≥ -3 + 4
Daí:
3sen x + 4 ≥ 1

E como y=3sen x +4, então encontramos que y ≥ 1.

Agora, a partir da expressão sen x ≤ 1, obteremos uma outra expressão de variação de
y.

Temos que sen x ≤ 1, se multiplicarmos por 4 ambos os lados, obteremos:
3.sen x ≤ 3.1
Daí:
3sen x ≤ 3

3sen x + 4 ≤ 3 + 4
Daí:
3sen x + 4 ≤ 7

www.pontodosconcursos.com.br - Prof. Sérgio Carvalho & Prof. Weber Campos


E como y=3sen x +4, então encontramos que y ≤ 7.

Dos resultados obtidos: y ≥ 1 e y ≤ 7, encontramos o intervalo de variação de y:

1 ≤ y ≤ 7 (Resposta!)

02. A expressão dada por y = –2senx + 5 é definida para todo número x real. Assim,
o intervalo de variação de y é
a) -1 ≤ y ≤ 7
b) y ≤ 3 ou y ≥ 7
c) 3 < y ≤ 5
d) 3 ≤ y ≤ 8
e) 3 ≤ y ≤ 7
Sol.:
A expressão fornecida no enunciado envolve a função seno. Assim, encontraremos o
intervalo de variação de y, a partir do intervalo de variação da função seno.
Da função seno, sabemos que o seu intervalo de variação é: [-1, 1], ou seja, o valor
máximo é 1, e o valor mínimo é -1. E podemos escrever que:
sen x ≥ -1 e sen x ≤ 1

A partir da expressão sen x ≥ -1, obteremos uma expressão de variação de y.

Temos que sen x ≥ -1 , se multiplicarmos por -2 ambos os lados, obteremos:
-2.sen x ≤ -2.(-1)

Observe que o sinal inverteu, era um sinal de “maior” e passou para um sinal de
“menor”, isso ocorreu porque multiplicamos por um valor negativo (-2).

Continuando, teremos: -2sen x ≤ 2

-2sen x + 5 ≤ 2 + 5
Daí:
-2sen x + 5 ≤ 7

E como y=-2sen x +5, então encontramos que y ≤ 7.

Agora, a partir da expressão sen x ≤ 1, obteremos uma outra expressão de variação de
y.

Temos que sen x ≤ 1, se multiplicarmos por -2 ambos os lados, obteremos:
-2.sen x ≥ -2.1
Novamente, invertemos o sinal, agora de menor para maior, porque multiplicamos por
um valor negativo (-2).

Continuando, teremos: -2sen x ≥ -2

-2sen x + 5 ≥ -2 + 5
Daí:
-2sen x + 5 ≥ 3

E como y=-2sen x +5, então encontramos que y ≥ 3.

Dos resultados obtidos: y ≥ 3 e y ≤ 7, encontramos o intervalo de variação de y:

3 ≤ y ≤ 7 (Resposta!)


03.(TFC 1995 ESAF) Simplificando a expressão (sen a. tg a. cossec a) / (cos a. cotg
a. sec a), obtém-se:
a) 0
b) 1
c) sen2a
d) sec2a
e) tg2a

Sol.:

O que temos que fazer para resolver esta questão é substituir as funções: tg, cossec,
cotg e sec, pelas funções seno e cosseno.

sen x cos x 1 1
Sabemos que: tg x = , cot g x = , sec x = e cos sec x = .
cos x sen x cos x sen x
A expressão dada no enunciado é: (sen a. tg a. cossec a) / (cos a. cotg a. sec a), se
colocarmos tudo em função do seno e cosseno, teremos:

sen a 1 cos a 1
(sen a. . ) / (cos a. . )
cos a sen a sen a cos a

sen a 1 cos a 1
(sen a. . ) / (cos a. . )
cos a sen a sen a cos a

sen a cos a
( / )
cos a sen a

sen a sen a
( x )
cos a cos a

sen 2 a
( ) ( tg 2 a ) (Resposta: alternativa E)
cos 2 a

04.(SERPRO 1996 ESAF) Se sen x = 0,5, então (1 / cotg x) vale:
a) 3
b) 3
3
c) 2
3
d) 3
2
e) 3
4
Sol.:
É bom iniciarmos a solução da questão definindo os quadrantes em que o ângulo x pode
estar. Como senx=0,5 , temos que o seno é positivo, daí o ângulo x pode está no 1º
quadrante ou no 2º quadrante.
cos x
A expressão dada no enunciado é: (1 / cotg x) , e sabemos que cot g x = . Daí, se
sen x
colocarmos a cotangente em função do seno e cosseno, teremos:

cos x sen x
(1 / ) ( )
sen x cos x


Para descobrirmos o valor da expressão acima, temos que achar o cosseno de x.

Pela relação fundamental: sen2x + cos2x = 1, podemos encontrar o valor do cosseno de
x a partir do valor do seno de x.

Temos que senx=1/2, substituindo esse valor na relação fundamental acima, teremos:

(1/2)2 + cos2x = 1 1/4 + cos2x = 1 cos2x = 1 - 1/4

cos2x = 3/4 cos x = 3/ 4 cos x = ± 3 /2

Obtemos dois valores para o cosseno de x, um positivo e outro negativo. Agora, temos
que analisar qual destes devemos escolher.

No início dessa solução, vimos que o ângulo x poderia estar no 1º quadrante ou no 2º
quadrante. Daí, faremos duas análises:

O valor do cosseno no 1º quadrante é positivo, daí se o x está no 1º quadrante, então
devemos escolher o valor positivo: cos x = 3 /2.

O valor do cosseno no 2º quadrante é negativo, daí se o x está no 2º quadrante, então
devemos escolher o valor negativo: cos x = - 3 /2.

A questão solicita o valor da expressão (1 / cotg x), que como já vimos é igual a:
sen x
. Substituiremos os valores do seno e cosseno nesta expressão.
cos x

Para senx=1/2 e cosx= 3 /2, teremos:

sen x 1/ 2 1 1× 3 3
= = = = (resposta para x no 1º quadrante)
cos x 3/2 3 3× 3 3

Para senx=1/2 e cosx= - 3 /2, teremos:

sen x 3
= – (resposta para x no 2º quadrante)
cos x 3

Portanto, temos duas respostas, porém a única que aparece nas alternativas é a
3
resposta . E é claro, devemos marcar a alternativa B.
3
A questão deveria ter definido qual era o quadrante de x para que tivéssemos somente
uma resposta!

05.(MPOG 2003 ESAF) Sabendo que x é o ângulo correspondente a um arco do
segundo quadrante, e que seno de x é igual a 12/13, então a tangente de x é
igual a:
a) –12/5
b) –10/13
c) 10/13
d) 12/13
e) 12/5

Sol.:


O enunciado informa que x é um ângulo do segundo quadrante, portanto a tangente de
x é um valor negativo. Assim, a alternativa correta ou é a A ou é a B.

Pela relação fundamental: sen2x + cos2x = 1, podemos encontrar o valor do cosseno de
x a partir do valor do seno de x.

Temos que senx=12/13, substituindo esse valor na relação fundamental acima,
teremos:

(12/13)2 + cos2x = 1 144/169 + cos2x = 1 cos2x = 1 – 144/169

cos2x = 25/169 cos x = 25 / 169 cos x = ± 5/13

No início dessa solução, já havíamos concluído que o cos x devia ser negativo. Portanto,
descartaremos o valor de +3/5, e a resposta será:

cos x = –3/5 (Resposta!)

06.(Especialista em Pol. Públicas e Gestão Governamental MPOG 2002 ESAF) Sabe-se
que a função inversa da função seno é a função cossecante e que o seno do dobro
de um arco é dado por sen 2x = 2sen x cos x. Sabendo-se que x é um arco do
segundo quadrante e que o cosseno da metade deste arco é igual a 1/3, então a
cossecante de x vale:
−2 3
a)
3
−2 2
b)
3
3
c)
3
2 3
d)
3
e) 1

Sol.:
O enunciado afirma que a função inversa da função seno é a função cossecante, isto
quer dizer que:
cossec x = 1 / sen x

Também o enunciado traz as seguintes informações:
sen 2x = 2senx . cosx
x é um arco do segundo quadrante
cos(x/2) = 1/3

Para calcularmos a cossecante de x, devemos obter primeiramente o valor do sen x.
Para isso, vamos utilizar as informações dadas no enunciado.

A equação sen 2x = 2senx.cosx pode ser escrita de maneira diferente, mas
equivalente, da seguinte forma: sen x = 2sen(x/2) . cos(x/2).

Desta última expressão, observamos que já temos o cos(x/2) e para calcularmos o
senx, necessitamos encontrar o valor do sen(x/2). Faremos isso através da relação
fundamental: sen2x + cos2x = 1.

Podemos escrever a relação fundamental acima da seguinte forma:
sen2(x/2)+cos2(x/2)=1. Substituiremos o valor de cos(x/2) nesta expressão.



sen2(x/2)+cos2(x/2)=1 sen2(x/2) + (1/3)2 = 1

sen2(x/2) = 1 – 1/9 sen2(x/2) = 8/9

8 2 2
sen(x/2) = ± sen(x/2) = ±
9 3

O seno de x/2 é positivo ou negativo? Como o x é um arco do 2º quadrante, então x/2
será do 1º quadrante e, portanto, o seno de x/2 é positivo. Daí, descartamos o valor negativo
acima e ficamos com:
2 2
sen(x/2) =
3

Agora é só substituir o valor do sen(x/2) e do cos(x/2) na expressão abaixo para
encontrarmos o valor do senx.
2 2 1
sen x = 2sen(x/2) . cos(x/2) sen x = 2 . .
3 3
4 2
sen x =
9

Daí, cossecante de x é igual a:
4 2
cossec x = 1 / sen x cossec x = 1 /
9

9 9 2
cossec x = cossec x = (Resposta!)
4 2 8

Observe que esta resposta não aparece entre as alternatives, foi por este motivo que a
ESAF teve que anular esta questão.

07.(TFC 1997 ESAF) Sabe-se que o seno do dobro de um ângulo α é igual ao dobro do
produto do seno de α pelo co-seno de α. Assim, sendo o seno de um ângulo de
120º igual a 3 2 , o seno de um ângulo de 240º é:
a) − 3 2 c) 3 e) 3 3
b) 3 2 d) 2 3

Sol.:

E enunciado traz a seguinte informação: sen 2α = 2senα.cosα. Nesta expressão,
fazendo α igual a 120º, podemos obter o seno de 240º.

sen 240º = 2.sen120º.cos120º

Falta calcular o valor do seno de 120º. Usaremos a relação fundamental:
sen2x+cos2x=1.

sen2120º + cos2120º = 1 ( 3 2 )2 + cos2120º = 1

cos2120º = 1 - 3 4 cos2120º = 1/4

cos 120º = ± 1/ 4 cos 120º = ± 1/2


O cosseno de 120º é positivo ou negativo? Como o ângulo de 120º é do 2º quadrante,
então o cosseno de 120º é negativo. Daí, descartamos o valor positivo acima e ficamos com:

cos 120º = –1/2

De posse do seno e do cosseno de 120º, já podemos obter o seno de 240º. Teremos:

sen 240º = 2.sen120º.cos120º sen 240º = 2. 3 2 .(–1/2)

sen 240º = – 3 2 (Resposta!)

08.(AFC-SFC 2001 ESAF) A condição necessária e suficiente para a identidade sen2α
= 2senα ser verdadeira é que α seja, em radianos, igual a:
a) π/3
b) π/2
c) n π sendo n um número inteiro qualquer
d) n π/2, sendo n um número inteiro qualquer
e) n π/3 ,sendo n um número inteiro qualquer

Sol.:
Uma das fórmulas apresentadas na aula dezesseis, e que já usamos em algumas
questões resolvidas acima, foi esta:
sen 2 x = 2 sen x cos x

Assim o valor de sen2α = 2senα.cosα . Substituiremos o valor de sen2α na expressão
dada no enunciado da questão.

sen2α = 2senα

2senαcosα = 2senα

2senαcosα – 2senα = 0

2senα(cosα – 1) = 0

O valor de α que satisfaz esta última expressão, pode ser obtido fazendo-se:

2senα=0 ou (cosα – 1)=0

1) Vamos calcular os valores de α para que 2senα=0.

2senα=0 senα=0

O seno é igual a zero para os arcos 0, ±π, ±2π, ±3π, ... . Generalizando:

α = kπ , onde k = 0, ±1, ±2, ...

2) Vamos calcular os valores de α para que (cosα – 1) = 0.

(cosα – 1) = 0 cosα = 1

O cosseno é igual a um para os arcos 0, ±2π, ±4π, ... . Generalizando:

α = k.2π , onde k = 0, ±1, ±2, ...


Resumindo:

Para que 2senα = 0 , devemos ter α = kπ , onde k é um inteiro qualquer.

Para que (cosα–1)=0 , devemos ter α = k.2π , onde k é um inteiro qualquer.

A solução é: α = kπ ou α = k.2π , mas como α=kπ também abrange os valores de
α=k.2π , então podemos dizer que a solução é simplesmente:

α = kπ , onde k é um inteiro qualquer (Resposta: alternativa C)

09.(SERPRO 1996 ESAF) Sendo p uma constante real, os valores de x e de y que
solucionam o sistema:

x.sen p – y.cos p = -cos 2p
x.cos p + y.sen p = sen 2p

a) (sen p,cos p)
b) (sen 2,cos 2p)
c) (sen 2p,cos p)
d) (sen p,-cos p)
e) (-sen p,-cos 2p)

Sol.:
Os valores de x e de y são as raízes do sistema.

Devemos elevar ao quadrado ambos os lados das equações do sistema, para que
possamos utilizar a relação fundamental: sen2p+cos2p=1 , e, assim, teremos:

(x.sen p – y.cos p)2 = (–cos 2p)2
(x.cos p + y.sen p)2 = (sen 2p)2

(x.sen p)2 – 2(x.sen p)(y.cos p) + (y.cos p)2 = (–cos 2p)2
(x.cos p)2 + 2(x.cos p)(y.sen p) + (y.sen p)2 = (sen 2p)2

x2.sen2p – 2xy.sen p.cos p + y2cos2p = cos22p
x2.cos2p + 2xy.cos p.sen p + y2.sen2p = sen22p

Somando membro a membro as duas equações do sistema, teremos:

x2.sen2p + x2.cos2p + 0 + y2cos2p + y2.sen2p = cos22p + sen22p

x2(sen2p + cos2p) + y2(cos2p + sen2p) = cos22p + sen22p

x2(1) + y2(1) = 1

x2 + y2 = 1

Os únicos valores de x e de y que satisfazem a equação x2 + y2 = 1 são os que são
apresentados na alternativa A e D, mas se substituímos o valor de x e de y da alternativa d na
segunda equação do sistema, verificaremos facilmente que estes valores não servem. Daí,
resposta: alternativa A.


10.(Oficial de Chancelaria MRE 2002 ESAF) Sabendo que x = 3sent e y = 4cost,
então, uma relação entre x e y, independente de t é dada por:
a) 16 y2 - 9 x2 = 144
b) 16 x2 - 9 y2 = 144
c) 16 y2 + 9 x2 = 144
d) 16 x2 + 9 y2 = 144
e) 9 y2 - 16 x2 = 144
Sol.:

Devemos elevar ao quadrado os valores de x e de y, para que possamos utilizar a
relação fundamental: sen2t+cos2t=1 . Fazendo isso, teremos:

x = 3sent x2 = (3sent)2 x2 = 9sen2t (1)

y = 4cost y2 = (4cost)2 y2 = 16cos2t (2)

Para que apareça a relação sen2t+cos2t=1 , devemos multiplicar a 1ª equação por 16
e a 2ª equação por 9, e depois somarmos as duas.

16x2 = 16.9sen2t 16x2 = 144sen2t

9y2 = 9.16cos2t 9y2 = 144cos2t

Somando, membro a membro, teremos:

16x2 + 9y2 = 144sen2t + 144cos2t

16x2 + 9y2 = 144(sen2t + cos2t)

16x2 + 9y2 = 144 (Resposta: alternativa D)

tgx. cot gx
11.Simplificando a expressão , obteremos:
sec 2 x − 1
2
a) sec x
2
b) cot g x
2
c) tg x
d) cos sec 2 x
2
e) cos x

Sol.:

Da aula dezesseis, temos as seguintes fórmulas que usaremos na solução dessa
questão, são elas:

cotgx = 1/tgx

tg 2 x + 1 = sec 2 x

Substituindo essas fórmulas na expressão do enunciado, teremos:

1
tgx.
tgx. cot gx tgx 1
cot g 2 x (Resposta: alternativa B)
sec 2 x − 1 2
tg x tg 2 x



12.Determine o valor de x e y nas figuras abaixo:

x

y 12

60o

20

Sol.:
x

y 12
y
60o
x
20 20 - x

12
y
60o

20 - x

3
Sabemos que: sen 60º = e que cos 60º = ½.
2

1) Cálculo de y

sen 60º = cateto oposto / hipotenusa

3
= y / 12 y= 6 3
2

2) Cálculo de x

cos 60º = cateto adjacente / hipotenusa

1/2 = (20-x) / 12 (20-x) = 6

x = 14

Agora, sim, falaremos sobre Geometria!


GEOMETRIA

1. ÂNGULOS

1.1. Definição
Ângulo é o nome que se dá à abertura formada por duas semi-retas que partem
de um mesmo ponto.

A

Indica-se por: AÔB ou α.
O α

B

Em que:

OA e OB são os lados do ângulo;
O é o vértice do ângulo.

1.2. Ângulo agudo

É aquele cuja medida é menor que a de um ângulo reto.

α

1.3. Ângulo obtuso

É aquele cuja medida é maior que a de um ângulo reto e menor que a de um
raso.

α

1.4. Ângulos opostos pelo vértice

β
γ α
θ

α e γ são opostos pelo vértice.
θ e β são opostos pelo vértice.

Dois ângulos opostos pelo vértice têm medidas iguais, ou seja, são
congruentes.


1.5. Bissetriz de um ângulo

Bissetriz de um ângulo é uma semi-reta de origem no vértice do ângulo que o
divide em dois ângulos congruentes.

α
bissetriz
β

α=β

1.6. Ângulos formados por duas retas paralelas interceptadas por uma
transversal

Duas retas paralelas r e s, interceptadas por uma transversal, determinam oito
ângulos, assim denominados:

t

b a
r
c d

β α
s
γ θ

ângulos correspondentes: a e α, b e β, c e γ, d e θ;
ângulos alternos internos: c e α, d e β;
ângulos alternos externos: a e γ, b e θ;
ângulos colaterais internos: c e β, d e α;
ângulos colaterais externos: a e θ, b e γ;

Propriedades:
Ângulos alternos internos são congruentes.
Ângulos alternos externos são congruentes.
Ângulos correspondentes são congruentes.
Ângulos colaterais internos são suplementares.
Ângulos colaterais externos são suplementares.


2. TEOREMA DE TALES

Um feixe de paralelas determina, em duas transversais quaisquer, segmentos
que são proporcionais.

t1 t2

A r1
D
r2
B E

r3
C F

AB DE
Posto isso, teremos: =
BC EF

Conseqüência: A
A

M N B C

B C M N

C B

A

M N

AM AN MN
Considerando que MN é paralelo a BC, então temos: = = .
AB AC BC

3. POLÍGONOS

3.1. Nomenclatura

Seja o polígono da figura:

A
D

B C


Em que:
A, B, C e D são os vértices do polígono.
AB, BC, CD e DA são os lados do polígono.

Alguns tipos de polígonos convexos:

triângulo – 3 lados
quadrilátero – 4 lados
pentágono – 5 lados
hexágono – 6 lados
decágono – 10 lados
icoságono – 20 lados

3.2. Número de diagonais de um polígono

O número de diagonais d de um polígono de n lados é dado por:

n(n − 3)
d=
2

3.3. Soma das Medidas dos ângulos Internos e Externos

e1
in en
i1
e2
i2 i5
e3 i3 e5
i4
e4

Soma dos ângulos internos de um polígono: Si = i1+i2+...+in = (n-2).180º

Soma dos ângulos externos de um polígono: Se = e1+e2+...+en = 360º

Observação:

Se o polígono for regular, ele tem todos os lados e os ângulos congruentes,
logo:
S
ângulo interno de um polígono de n lados: i
n

360º
ângulo externo de um polígono de n lados:
2



4. TRIÂNGULOS

4.1. Classificação:

Eqüilátero: tem os três lados iguais e os três ângulos iguais (60º).

Isóceles: tem dois lados iguais e dois ângulos iguais.

Escaleno: os três lados são diferentes e também os três ângulos.

4.2. Relações no triângulo qualquer:
B

a c

C A
b
1) Qualquer lado é menor que a soma dos outros dois:
a<b+c
b<a+c
c<a+b

2) A soma dos ângulos internos é 180°:
) ) )
A + B + C = 180º

4.3. Mediana

È o segmento que une um vértice ao ponto médio do lado oposto.

B

mediana
A C
M


4.4. Altura

É o segmento que parte de um vértice e é perpendicular ao lado oposto.

B B

altura
altura

A C C
H H A

4.5. Bissetriz

A bissetriz do ângulo Â divide este ângulo em duas partes iguais e intercepta o
lado oposto no ponto D. O segmento AD denomina-se bissetriz interna relativa ao
vértice A.
A

C B
D

Teorema da bissetriz interna: a bissetriz do ângulo interno de um
triângulo determina sobre o lado oposto dois segmentos proporcionais aos
outros dois lados.

BD AB
Da figura acima, temos: =
DC AC

4.6. Semelhança de Triângulos

Dois triângulos ABC e A’B’C’ são dito semelhantes, se:
) ) ) ) ) )
• os ângulos correspondentes forem congruentes ( A = A' , B = B' e C = C' ).
a b c
• os lados correspondentes forem proporcionais ( = = ).
a ' b' c '
A’
A

b c b’ c’

C B
a B’
C’
a’


4.7. Relações Métricas no Triângulo Retângulo

c b
h

m n
a

a – hipotenusa
b e c – catetos
h – altura relativa a hipotenusa
m e n – projeções dos catetos sobre a hipotenusa

Relações métricas:
1) bc = ah 2) c2 = a.m 3) b2 = a.n 4) h2 = m.n

Teorema de Pitágoras: a2 = b2 + c2

5. QUADRILÁTEROS

Quadrilátero é o polígono de quatro lados.

A soma dos ângulos internos de um quadrilátero é: 360º.

i1 i4
i1 + i2 + i3 + i4 = 360º
i2

i3

5.1. Classificação

Paralelogramo
É o quadrilátero cujos lados opostos são paralelos.

Os ângulos opostos são congruentes.

Paralelogramos Notáveis

Retângulo: é o paralelogramo que tem os quatro ângulos congruentes e de
medida igual a 90º.


Losango: é o paralelogramo que tem os quatro lados iguais.

Quadrado: é o paralelogramo que tem os quatro lados e os quatro ângulos
iguais entre si.

Trapézio
É o quadrilátero em que apenas dois lados são paralelos entre si.
D C

A B
H

AB é paralela a CD.
AB é a base maior.
CD é a base menor.
DH é a altura.

Propriedade:

D C
ponto médio
ponto médio
M N

A B
AB + CD
MN =
2

6. Ângulos na Circunferência

6.1. Ângulo Central

É todo ângulo cujo vértice coincide com o centro da circunferência.

B

O α α = AB

A

A medida de um ângulo central é igual à medida do arco que ele enxerga.



6.2. Ângulo inscrito

B

α = AB
V α
2
A

A medida de um ângulo inscrito é igual à medida do arco que ele enxerga.

Se AB corresponde à metade da circunferência (180º), então o ângulo α é
reto.

O triângulo inscrito é retângulo.
A B
O

6.3. Ângulo de Vértice Interno

C B
V
α α = AB + CD
D 2
A

A medida de um ângulo de vértice interno à circunferência é igual a semi-soma
das medidas dos arcos determinados pelos seus lados.

6.4. Ângulo de Vértice Externo

C B
V α α = AB - CD
D 2
A

A medida de um ângulo de vértice externo à circunferência é igual a
semi-diferença das medidas dos arcos determinados pelos seus lados.

6.5. Ângulo de Segmento

É todo ângulo cujo vértice pertence à circunferência, sendo um de seus lados
secante e o outro, tangente à circunferência.



A V=B
α α = AB
2

A medida de um ângulo de segmento é igual a metade do arco por ele
determinado.

7. ÁREAS DAS FIGURAS PLANAS

Retângulo:

b área = a . b

a
Quadrado:

a
área = a2

a

Paralelogramo:

b
h área = base x altura = a x h

a
Trapézio:

b

área = (B + b).h
c d
h 2

B
Losango:

a a
d área = D . d
D 2
d = diagonal menor
a a
D = diagonal maior


Triângulo:

c b
h área = base x altura = a x h ou
2 2
α
área = a.b.senα
a
2
Triângulo Eqüilátero:

a a
h a 3 a2 3
h= e área =
2 4

a
Área do Círculo

r área = πr2
O
Comprimento de uma circunferência:
C = 2πr

Setor Circular:

l
r
α área = απr2_
360º

Hexágono Regular: no seu interior há seis triângulos equiláteros

a

a a a2 3
área = 6 ×
4

a a a a

a


8. VOLUME DOS SÓLIDOS

Paralelepípedo retângulo

Volume = área da base x altura = a . b . c

c Área total = 2(ab +ac + bc)
b b
a

Cubo

Volume = área da base x altura = a2. a = a3

a Área total = área da base x altura = 6a2
a
a

Cilindro

Área lateral = 2πr . h

h Área total = área lateral + área das bases = 2πrh + 2πr2
h
Volume = área da base x altura = πr2 . h
r

Esfera
R = raio da esfera

Área total = 4π R 2
4πR 3
Volume =
3

Pirâmide (tetraedro regular: as faces são triângulos equiláteros)

Volume = área da base x altura
3
h

a2 3
×h
Volume = 4
3



Cone

Volume = área da base x altura = πr2 . h
h
3 3

r

Partiremos direto para o dever de casa, na próxima aula traremos todas as
questões resolvidas.

DEVER DE CASA DE GEOMETRIA BÁSICA

01. (AFTN 1998/ESAF) Em um triângulo retângulo, um dos catetos forma com a
hipotenusa um ângulo de 45º. Sendo a área do triângulo igual a 8 cm2, então a
soma das medidas dos catetos é igual a:
a) 8 cm2 d) 16 cm2
b) 16 cm e) 8 cm
c) 4 cm

02. (Esp. em Pol. Públicas e Gestão Governamental MPOG/2000 ESAF) Os catetos
de um triângulo retângulo medem, respectivamente, A+X e A+Y, onde A, X e Y
são números reais. Sabendo que o ângulo oposto ao cateto que mede A+X é igual
a 45º, segue-se que:
a) Y = -2 X d) Y = X
b) Y = (31/2)/2 X e) Y = 2 X
c) Y = 31/2 X

03. (AFC-STN-2000 ESAF) Os catetos de um triângulo retângulo medem,
respectivamente, x e (y-2). Sabendo que a tangente trigonométrica do ângulo
oposto ao cateto que mede x é igual a 1, então o perímetro do triângulo é igual a
a) 2y (x + 1) d) 2 (x + y)
b) y (2 + 2 2 ) e) x2 + y2
c) x (2 + 2 )

04. (AFTN 1998/ESAF) Um trapézio ABCD possui base maior igual a 20 cm, base
menor igual a 8 cm e altura igual a 15 cm. Assim, a altura, em cm, do triângulo
limitado pela base menor e o prolongamento dos lados não paralelos do trapézio é
igual a:
a) 10 d) 17
b) 5 e) 12
c) 7


05. (Esp. em Pol. Públicas e Gestão Governamental MPOG/2000 ESAF) Em um
triângulo eqüilátero de lado igual a 12 cm, traça-se um segmento XY paralelo ao
lado BC de modo que o triângulo fique decomposto em um trapézio e em um novo
triângulo. Sabendo-se que o perímetro do trapézio é igual ao perímetro do novo
triângulo, então o comprimento do segmento de reta XY , em centímetros, vale
a) 5 c) 9 e) 12
b) 6 d) 10

06. (TFC 1996 ESAF) Os pontos X, Y e Z estão todos no mesmo plano. A distância,
em linha reta, do ponto X ao ponto Y é de 30 cm, e do ponto X ao ponto Z é de 22
cm. Se d é a distância em centímetros, também em linha reta, do ponto Y ao
ponto Z, então o conjunto dos possíveis valores para d é dado por:
a) 8 ≤ d ≤ 30 d) 22 ≤ d ≤ 52
b) 8 ≤ d ≤ 52 e) 30 ≤ d ≤ 52
c) 22 ≤ d ≤ 30

07. (TCU 2002 ESAF) As medidas dos ângulos do triângulo AYG são tais que Â < Y
< 90° e G > 90°. As bissetrizes externas dos ângulos Â e G cortam os
prolongamentos dos lados opostos YG e AY nos pontos P e Q, respectivamente.
Sabendo que, AG = GQ = AP, então a soma dos ângulos Y e G é igual a:
a) 48° d) 148°
b) 64° e) 168°
c) 144°

08. (Oficial de Chancelaria MRE 2002 ESAF) O ângulo A de um triângulo qualquer
ABC mede 76°. Assim, o menor ângulo formado pelas bissetrizes externas relativas
aos vértices B e C deste triângulo vale:
a) 50° d) 64°
b) 52° e) 128°
c) 56°

09. (Assistente de Chancelaria MRE 2002) Num triângulo ABC, o ângulo interno de
vértice A mede 60°. O maior ângulo formado pelas bissetrizes dos ângulos internos
de vértices B e C mede:
a) 45° c) 90° e) 150°
b) 60° d) 120°

10. (Especialista em Pol. Públicas e Gestão Governamental MPOG 2002 ESAF) Se o
raio de uma circunferência tiver um acréscimo de 50%, então o acréscimo
percentual em seu comprimento será igual a:
a) 25% d) 80%
b) 50% e) 85%
c) 75%

11. (TFC/SFC 2001 ESAF) As rodas de um automóvel têm 40 cm de raio. Sabendo-
se que cada roda deu 20.000 voltas, então a distância percorrida pelo automóvel,
em quilômetros(Km), foi de:
a) 16 Km d) 1,6 . 103π Km
b) 16 π Km e) 1,6 . 103π2 Km
2
c) 16 π Km


12. (AFC 2002 ESAF) A circunferência é uma figura constituída de infinitos pontos,
que tem a seguinte propriedade: a distância de qualquer ponto P(x,y), da
circunferência até o seu centro C(a,b) é sempre igual ao seu raio R. A forma geral
da circunferência é dada por: (x - a)2 + (y - b)2 = R2. Assim, a equação da
circunferência de centro na origem dos eixos e que passa pelo ponto (3,4) é:
a) x2 + y2 = 4 d) x2 + y2 = 25
2 2
b) x + y = 9 e) x2 + y2 = 49
c) x2 + y2 = 16

13. (AFC 2005 ESAF) Um feixe de 4 retas paralelas determina sobre uma reta
transversal, A, segmentos que medem 2 cm, 10 cm e 18 cm, respectivamente.
Esse mesmo feixe de retas paralelas determina sobre uma reta transversal, B,
outros três segmentos. Sabe-se que o segmento da transversal B, compreendido
entre a primeira e a quarta paralela, mede 90 cm. Desse modo, as medidas, em
centímetros, dos segmentos sobre a transversal B são iguais a:
a) 6, 30 e 54 d) 14, 26 e 50
b) 6, 34 e 50 e) 14, 20 e 56
c) 10, 30 e 50

14. (Analista de Recursos Financeiros SERPRO 2001 ESAF) Um triângulo tem lados
que medem, respectivamente, 6m, 8m e 10m. Um segundo triângulo, que é um
triângulo semelhante ao primeiro, tem perímetro igual a 12m. A área do segundo
triângulo será igual a:
a) 6 m2 d) 48 m2
2
b) 12 m e) 60 m2
c) 24 m2

15. (AFC 2005 ESAF) Em um triângulo ABC qualquer, um dos lados mede 2 cm e
um outro mede 2 cm. Se o ângulo formado por esses dois lados mede 45°, então a
área do triângulo é igual a
a) 3−1 3 c) 2 −1 2 e) 1
b) 21 2 d) 3 2

16. (Oficial de Chancelaria MRE 2002 ESAF) Um trapézio ABCD, com altura igual a
h, possui bases AB = a e CD = b, com a > b. As diagonais deste trapézio
determinam quatro triângulos. A diferença entre as áreas dos triângulos que têm
por bases AB e CD respectivamente e por vértices opostos a interseção das
diagonais do trapézio é igual a:
( a + b) ( a − b) h (b − a )h
a) c) e)
2 2 2
( a + b) h ( a − b)
b) d)
2 2

17. (AFC-SFC 2001 ESAF) Um hexágono é regular quando, unindo-se seu centro a
cada um de seus vértices, obtém-se seis triângulos equiláteros. Desse modo, se o
lado de um dos triângulos assim obtidos é igual a 3 / 2 m, então a área, em
metros, do hexágono é igual a:
a) 9 3 d) 3 3
4
7 3
b) e)
3 3
c) 2 3


18. (TCE-RN 2000/ESAF) A reta R1, que possui coeficiente linear igual a 8 e que é
perpendicular à reta R2= -1/3 x + 8, forma com os eixos coordenados e com a
reta x = 2 uma figura cuja área, em metros quadrados, é igual a:
a) 16 d) 48
b) 18 e) 50
c) 22

19. (TTN 1998 ESAF) A área de um círculo localizado no segundo quadrante e cuja
circunferência tangencia os eixos coordenados nos pontos (0,4) e (- 4,0) é dada
por
a) 16 π b) 4 π c) 8 π d) 2 π e) 32 π

20. (AFC 2002 ESAF) Um dos lados de um retângulo é 7 cm maior do que o outro
lado. Se a diagonal deste retângulo mede 13 cm, então o volume de um prisma
regular, de 5 cm de altura, e que tem como base este retângulo, é igual a:
a) 50 cm3 c) 150 cm3 e) 300 cm3
b) 65 cm3 d) 200 cm3

21. (Fiscal do Trabalho 2003 ESAF) Fernando, João Guilherme e Bruno encontram-
se perdidos, uns dos outros, no meio da floresta. Cada um está parado em um
ponto, gritando o mais alto possível, para que os outros possam localizá-lo. Há um
único ponto em que é possível ouvir simultaneamente Fernando e Bruno, um outro
único ponto (diferente daquele) em que é possível ouvir simultaneamente Bruno e
João Guilherme, e há ainda um outro único ponto (diferente dos outros dois) em
que é possível ouvir simultaneamente João Guilherme e Fernando. Bruno encontra-
se, em linha reta, a 650 metros do ponto onde se encontra Fernando. Fernando,
por sua vez, está a 350 metros, também em linha reta, do ponto onde está João
Guilherme. Fernando grita o suficiente para que seja possível ouvi-lo em qualquer
ponto até uma distância de 250 metros de onde ele se encontra. Portanto, a
distância em linha reta, em metros, entre os pontos em que se encontram Bruno e
João Guilherme é:
a) 650 b) 600 c) 500 d) 700 e) 720

22. (Fiscal do Trabalho 2003 ESAF) Augusto, Vinicius e Romeu estão no mesmo
vértice de um polígono regular. Num dado momento, os três começam a caminhar
na borda do polígono. Todos os três caminham em velocidades constantes, sendo
que a velocidade de Augusto é o dobro da de Vinicius e o quádruplo da de Romeu.
Augusto desloca-se em sentido oposto ao de Vinicius e ao de Romeu. Após um
certo tempo, Augusto e Vinicius encontram-se num determinado vértice. Logo a
seguir, exatamente dois vértices depois, encontram-se Augusto e Romeu. O
número de arestas do polígono é:
a) 10 b) 15 c) 12 d) 14 e) 11

23. (SERPRO 1996 ESAF) O ponto de intersecção das retas 2x + y – 1 = 0 e x – y
+ 16 = 0 têm coordenadas iguais a:
a) (-11,-5) d) (11,5)
b) (-11,3) e) (-5,11)
c) (-5,-1)

24. (AFC-SFC 2001 ESAF) Sabe-se que as retas de equações r1 = αx e r2 = -2x+β
interceptam-se em um ponto P(x<0; y<0). Logo,
a) α > 0 e β > 0 d) α < -1 e β < 0
b) α > 0 e β < 0 e) α > -1 e β > 0
c) α < 0 e β < 0


Aula 17 geometria básica

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Aula 17 geometria básica

Mais de J M

Aula 17 geometria básica