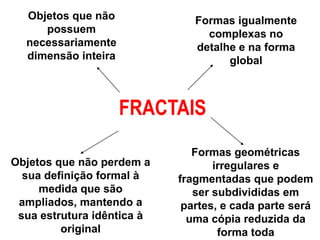
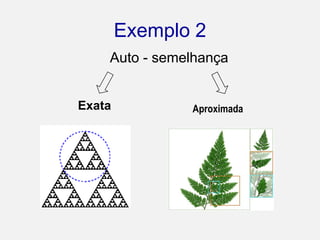
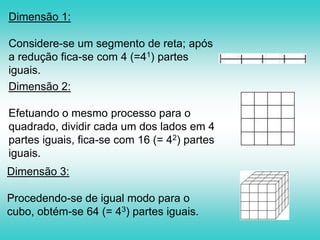
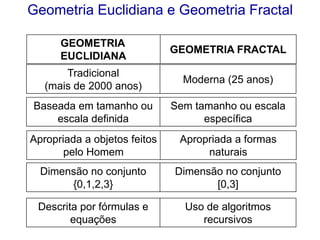
O documento explora a relação entre geometria euclidiana e não-euclidiana, com ênfase na importância dos fractais na matemática e no ensino. Discute a evolução do pensamento geométrico desde Euclides até contribuições modernas de Mandelbrot, abordando propriedades e aplicações dos fractais no contexto educacional. Sugestões de atividades práticas são apresentadas para integrar conceitos de fractais nas disciplinas escolares, promovendo uma compreensão mais ampla da geometria.

1. A Magia dos Franciele Buss Frescki KestringPriscila Pigatto

2. ProblematizaçãoQue equação matemática representa a estrutura de uma nuvem? Que sólidos geométrico melhor representa uma montanha? Qual é o comprimento da costa brasileira? Como podemos explicar matematicamente as ramificações dos vasos sanguíneos? Quais as formas de reprodução de uma bactéria numa lâmina de laboratório em função dos alimentos? Como prever a evolução de uma empresa?

3. Euclides330-260 a.C.Há mais de dois mil anos, Euclides, segundo conta a tradição, enquanto caminhava pela praia, notou que a areia, vista como um todo, se assemelhava a uma superfície contínua e uniforme, embora fosse composta por pequenas partes visíveis. Desde então, empenhou-se em tentar provar, matematicamente, que todas as formas da natureza podiam ser reduzidas a formas geométricas simples.

4. Concentrado sobretudo nas formas, deixou de lado um elemento importantíssimo neste tipo de análise: a dimensão.No entanto, inconscientemente, esta foi a chave para o pensamento inicial de Euclides, já que um grão de areia, considerado isoladamente, apresenta três dimensões (largura, altura e profundidade), enquanto que a superfície arenosa da praia é visualmente plana (com duas dimensões).

5. Para Euclides, os objectos da Natureza podiam ser representados como formas geométricas simples, como quadrados, circunferências, etc...

6. Geometria EuclidianaO quinto postulado de Euclides equivale ao axioma das paralelas; Por um ponto exterior a uma reta, apenas passa uma outra reta paralela à dada;Este postulado foi objeto de polêmica por não possuir o mesmo grau de "evidência" que os outros postulados

7. Geometria Século XIX que Karl Friedrich Gauss, Janos Bolyai, Bernard Diemann e Nicolai Ivanovich Lobachevski demonstraram que se trata efetivamente de um axioma, necessário e independente dos outros; Supuseram que o postulado de Euclides não era verdadeiro e substituíram-no por outros axiomas:

8. GeometriaSubstituindo o axioma das paralelas, era possível construir duas geometrias diferentes da geometria euclidiana, igualmente coerentes e que não conduziam a nenhuma contradição;Desde então, encontramo-nos perante três sistemas geométricos diferentes:

9. GeometriaGeometria euclidiana, por vez chamada parabólica;A geometria de Lobachevski, também chamada hiperbólica;A geometria do Riemann, também chamada elíptica ou esférica.

10. GeometriaAs duas últimas recebem o nome de geometrias não euclidianas;Permitiram às ciências exatas do século XX uma série de avanços, entre os quais a elaboração da Teoria da Relatividade de Einstein (1879 - 1955);

11. GeometriaA geometria não-euclidiana se divide em vários segmentos:A geometria fractal;A geometria projetiva;A geometria esférica; A geometria hiperbólica

12. Diretrizes Curriculares da Matemática para Educação Básica do Estado do Paraná“[...] o conteúdo estruturante geometrias se desdobra nos seguintes conteúdos específicos: Geometria Plana; Geometria Espacial; Geometria Analítica, e noções básicas de Geometria Não-euclidiana.”, ou seja, o aluno deve ter conhecimento mais amplo da geometria, não se fixando apenas na Geometria Euclidiana, mas congregando, também, ao seu saber, noções da Geometria Não-euclidiana.

13. VídeosFractais na natureza;Dimensão oculta;

14. Como surgiram os fractais?Benoit Mandelbrot Nasceu a 20 de Novembro de 1924 na Polónia;

15. Formação Académica realizada em França;

16. Grande gosto pela geometria, procurando resolver muitos problemas matemáticos com base na mesma;No início dos anos 80, nomeou (ao invés de descobrir ou inventar) os fractais, para classificar certos objetos que não possuíam necessariamente dimensão inteira, podendo ter dimensão fracinária.

17. “Nuvens não são esferas, montanhas não são cones, continentes não são círculos e nem o raio viaja em linha reta." Benoit Mandelbrot (The Fractal Geometry of Nature - 1983)

18. Como surgiu a palavra FractalEmbora os “monstros matemáticos” existissem há muito tempo, ainda ninguém lhes tinha atribuído nenhum nome. Foi então que Benoit Mandelbrot, ao preparar a sua primeira obra sobre os ditos“monstros”, sentiu necessidade de lhes atribuir um nome.verbo frangere (que significa quebrar, fraturar, irregular)FRACTALadjetivo fractus

19. Objetos que não possuem necessariamente dimensão inteiraFormas igualmente complexas no detalhe e na forma globalFRACTAISFormas geométricas irregulares e fragmentadas que podem ser subdivididas em partes, e cada parte será uma cópia reduzida da forma todaObjetos que não perdem a sua definição formal à medida que são ampliados, mantendo a sua estrutura idêntica à original

20. Importância dos Fractais em sala de aula Segundo Barbosa (2002) a utilização de fractais em sala de aula no Ensino Fundamental e Médio é importante pelas seguintes razões: a) estabelece conexões com várias ciências; b) mostra deficiências da Geometria Euclidiana para o estudo de formas da natureza;

21. Importância dos Fractais em sala de aula c) utiliza a difusão e acesso às tecnologias computacionais nos vários níveis de escolaridade; d) explora a beleza dos fractais para o desenvolvimento do senso estético; e) desenvolve a curiosidade, face ao caráter inesperado de cada iteração.

22. Propriedades dos FractaisAuto-similaridade: pode ser exata ou estatística, ou seja, mantém a mesma forma e estrutura sob uma transformação de escala (transformação que reduz ou amplia o objeto ou parte dele);Exemplo 1Têm infinitos detalhes;São geralmente auto-semelhantesNão dependem de escala

23. Exemplo 2Auto - semelhançaExataAproximada

24. Propriedades dos FractaisComplexidade infinita, isto é, qualquer que seja o número de amplificações de um objeto fractal, nunca obteremos a “imagem final”, uma vez que ela poderá continuar a ser infinitamente ampliada

25. Propriedades dos FractaisIrregularidade, no sentido de rugosidade (não-suavidade) ou fragmentação;Possuir em geral, dimensão não-inteira. A dimensão fractal quantifica, de certo modo, o grau de irregularidade ou fragmentação do conjunto considerado.

26. Dimensão Da Geometria Euclidiana sabemos que: Um ponto é o que não tem parte, isto é, tem dimensão zero; Uma linha é um comprimento sem largura, ou seja, tem dimensão um;  Uma superfície é o que só tem comprimento e largura (dimensão dois); Um sólido é o que tem comprimento, largura e profundidade (dimensão 3).

27. A dimensão de um objeto, ao contrário do que sucede na Geometria Euclidiana, não é necessariamente um número inteiro. Com efeito, ela pode ser um número fracionário. A dimensão de um fractal representa o grau de ocupação deste no espaço, estando relacionada com o seu grau de irregularidade. Definimos então dimensão de uma curva fractal como sendo um número que caracteriza a maneira na qual a medida do comprimento entre dois pontos aumenta à medida que a escala diminui.

28. Dimensão 1:Considere-se um segmento de reta; após a redução fica-se com 4 (=41) partes iguais.Dimensão 2:Efetuando o mesmo processo para o quadrado, dividir cada um dos lados em 4 partes iguais, fica-se com 16 (= 42) partes iguais.Dimensão 3:Procedendo-se de igual modo para o cubo, obtém-se 64 (= 43) partes iguais.

29. Sejam: N = número de partes em que se divide o objeto; r = coeficiente de redução. Dimensão 1 Dimensão 2 Dimensão 3

30. Generalizando:(d é a dimensão do objeto em estudo)Este raciocínio é válido para qualquer redução efetuada em objetos com auto-semelhança exata.

31. Geometria Euclidiana e Geometria Fractal

32. Observe as seguintes figuras

33. Observe as seguintes figuras

34. Observe as seguintes figuras

35. Atividade 1Cite uma característica que você observou nas figuras mostradas;

36. Vídeo UFPR;Atividades propostas para sala de aula

37. Atividade 2Construção de cartões

38. xa/2ax/4Passo 1: com a folha em pé dobrar ao meio, ao meio novamente, vincar e desdobrar.Com a folha deitada, fazer o mesmo e recortar em ¼ dos dois lados, até a marca feita.

39. Após recortar, encerramos a iteração nº 1.Abrindo a folha e dobrando o recorte para dentro, teremos o seguinte:

40. a/4a/2aVamos repetir o passo 1, tomando como princípio a parte que está dobrada para cima

41. A segunda iteração está pronta:(lembre-se de dobrar os novos recortes para dentro!)

42. Continue repetindo as iterações quantas vezes conseguir.A final, você terá um cartão fractal, conhecido por Degraus fractais.Para que ele fique firme, cole-o numa folha do mesmo tamanho (A4).

44. Triângulo de Sierpinski

45. VídeoConstrução do triângulo de Sierpinski;

46. Atividade 3Construção do Triângulo de Sierpinski;Material: 1 triângulo com 32cm de lado (vermelho) 1 triângulo com 16cm de lado (amarelo) 3 triângulos com 8cm de lado (amarelo) 9 triângulos com 4cm de lado (amarelo)

47. Encontrar o ponto médio do triângulo de 32 cm de lado (vermelho);Colar os triângulos amarelos;E o processo se repete sucessivamente Passos para a construção do triângulo de Sierpinski

48. Conteúdos relacionados com FractaisProporcionalidade;Área;Perímetro;Progressão Aritmética;Progressão Geométrica;Potenciação;

49. Plano de trabalho docente SérieConteúdo EstruturanteConteúdo específicoJustificativaEncaminhamentos metodológicosCritérios e instrumentos de avaliaçãoReferências

50. Ideias...Conteúdo Estruturante:GeometriasConteúdo Básico:Geometrias não-euclidianaConteúdo Específico:Conceitos de Geometria Fractal

51. Possíveis Relações Interdisciplinares:Ciências, Geografia, ArtesPossíveis Articulações de Conteúdos:Números e Álgebra, Geometrias e Grandezas e Medidas (varia conforme a série abordada)

52. JustificativaNo estudo da geometria existem situações em que a Geometria Euclidiana torna-se insuficiente para responder algumas situações, para tal se torna necessário o estudo da geometria fractal, conforme vimos anteriormente.

53. Encaminhamentos metodológicosDaremos sugestões de atividades que podem ser realizadas nas diferentes séries, nada impedindo que possam ser adaptadas e trabalhadas de outra maneira.

54. Os conceitos de geometria fractal podem ser trabalhados em qualquer série, por si mesmos ou articulando com outros conteúdos.

55. SugestõesPassar na TV multimídia imagens da natureza com características fractais (procurar na rede, no dia-a-dia).Ver vídeos sobre fractais.Isto pode ser trazido pelo professor, ou mesmo pesquisado no laboratório de informática.

63. Fractais gerados por computadorNo Paraná Digital está disponível o software Xaos, que cria fractais a partir de iteraçõesÉ uma boa articulação com os conteúdos de artes.Algumas imagens:

72. 5ª série Frações, Potenciação, Medidas de comprimentoTrabalhar com o triângulo de Sierpinski

73. 6ª SérieApresentar imagens do Triângulo de Sierpinski e propor a construção de maneiras variadas (quebra-cabeça e desenho);

74. Nível 0

75. Nível 1

76. Nível 2

77. Nível 3

78. Nível 4

79. Sugestão de ConteúdosNúmeros e Álgebra:Razão e Proporção;Grandezas e Medidas: Ângulos ;Geometrias: Geometria Plana

80. 7ª SérieAtividade: Construção do Floco de Neve de Koch;Discussão das etapas envolvidas formalizando os conceitos.

82. Sugestão de Conteúdos Grandezas e Medidas:Medidas de comprimento;Medidas de área.Números e Álgebra:Números racionais;Potências.GeometriasGeometria Plana.

83. AtividadeA geometria fractal é conteúdo básico da 7ª série, portanto pode-se propor uma atividade onde os alunos criem o seu fractal, utilizando formas geométricas que eles conheçam.

84. 8ª SérieApresentação e discussão da Árvore Pitagórica

86. Sugestão de ConteúdosGrandezas e Medidas:Relações métricas no triângulo retângulo;Trigonometria no triângulo retângulo.Números e Álgebra:Teorema de Pitágoras.Geometrias:Geometria Plana.

87. Outras atividades que podem ser abordadas em qualquer sérieFractal TriminóConstrução:1. Considere o triminó não-reto, construído por 3 quadrados , que serão fractal em nível 1.2. O aluno deverá substituir cada peça quadrada por um triminó L , teremos assim o Fractal em nível 2.

88. 3. Novamente o aluno deverá trocar cada quadrado por um triminó, obtendo assim o Fractal ao nível 3.Construa o Fractal Triminó ao Nível 4.- Quantas peças foram usadas?- Para construir um Fractal Triminó ao Nível 5, quantas peças serão necessárias?- E para construir um Fractal Triminó ao Nível n?- Agora você e capaz de descobrir que conteúdo da matemática está relacionado com esta atividade?- Qual o perímetro em cada nível? Considere cada peça quadrada com 2,5 cm de lado.

89. A construção do fractal triminó prioriza alguns objetivos como: reconhecer uma sequência numérica, estimar a quantidade de peças em cada iteração, organizar dados em tabelas, calcular perímetro, etc.

90. Cartão FractalPode ser trabalhado em qualquer série, abordando os conceitos de fractal e suas propriedades e proporcionalidade.

93. Outros Cartões

96. Ensino MédioOs conteúdos a serem abordados:Função;Progressão Aritmética ou GeométricaTriângulo de Pascal

97. A computação gráfica é uma área que se encontra em franca expansão. O que muita gente não sabe é que algumas das imagens mais belas e complexas são feitas por processos simples que se repetem várias vezes. Veja as etapas de criação do ramo abaixo:

99. Sugestão de ConteúdosFunção Exponencial;Progressão Geométrica

100. Qual a relação do Triângulo de Sierpinski com o Triângulo de Pascal?

101. O importante desta atividade é observar como estes dois triângulos estão intimamente ligados, apesar de que aparentemente não parecer que se relacionam, visto que um deles é um “amontoado” de números e o outro contém no seu interior um padrão geométrico.

102. Atividade1. Construir o Triângulo de Pascal com pelo menos 8 ou 16 linhas( pode usar a malha de triângulos equiláteros ou hexágonos).2. Colorir em preto as casas correspondentes aos números ímpares.3. Que observas?

103. AtividadePara essa atividade é necessário explicar o Triângulo Aritmético de Pascal, sua formação, descoberta e propriedades. Como por exemplo: as diagonais de forasão formadas pelo número 1 e que a soma de dois números consecutivos de uma mesma linha do triângulo corresponde ao número que está na linha logo abaixo,bem abaixo dos dois números somados, outra propriedade é que a soma dos elementos de cada linha é uma potência de base 2. Não esquecendo que na segunda diagonal encontram-se os números naturais.