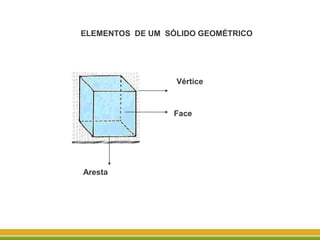
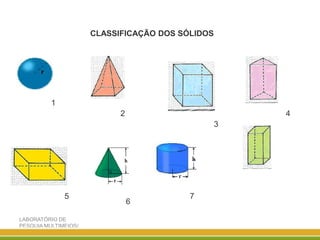
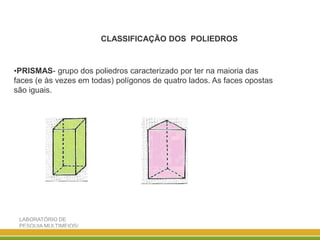
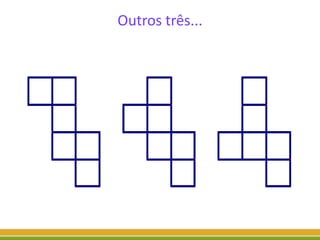
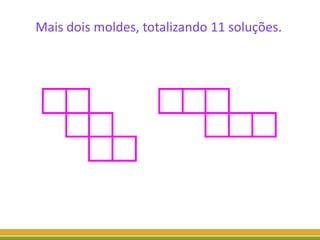
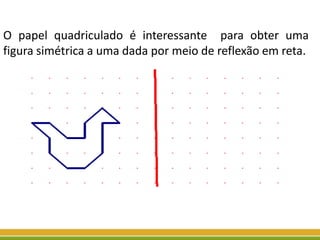
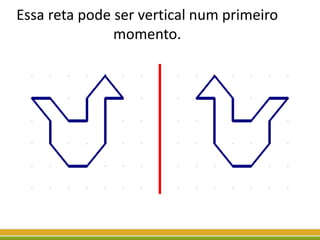
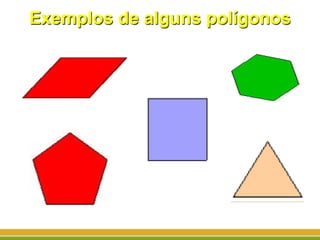
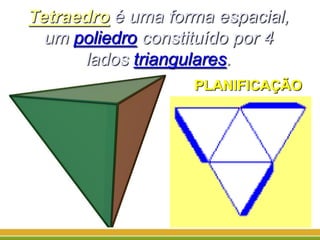
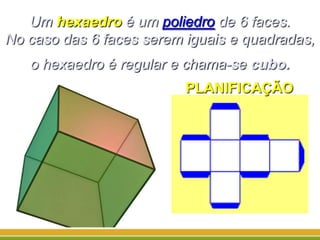
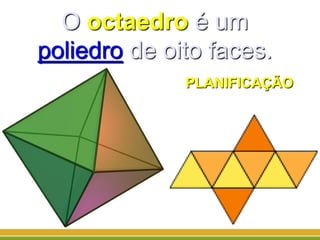
O documento discute a geometria, começando com sua origem na Grécia antiga e conceitos como pontos, retas, planos e figuras geométricas. Também aborda a geometria euclidiana, não-euclidiana, plana, espacial e escolar, além de figuras como triângulos, polígonos, poliedros e suas classificações.

1. GEOMETRIA
CADERNO 5
PNAIC - UFC

2. http://www.youtube.com/watch?v=Kiok0T2WHf4

3. ORIGEM DA GEOMETRIA?
Um pouco de história

4. O que significa Geometria?
Resulta de dois termos gregos:
GEO- terra
METRIA- medir

5. GEOMETRIA- é o ramo da matemática relacionado com as propriedades do
espaço, normalmente em termos de figuras do plano (bidimensional) e
sólidas(tridimensional).
Divide-se em geometria pura, que se dedica ao plano e à geometria dos
sólidos, tratada na obra de Euclides (ELEMENTOS) e geometria analítica ou
de coordenadas e ainda uma terceira a geometria não-euclidiana.

6. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
O historiador grego Heródoto (500 a.C.) atribuiu aos egípcios o início da
geometria, mas outras civilizações antigas (babilônios, hindus, chineses)
também possuíam muitas informações geométricas. Os conceitos de Geometria
surgem na Grécia. Para entrar na escola de Platão era preciso ter
conhecimentos geométricos, nesse contexto sobressaem Tales de Mileto (um
dos sete sábios da Grécia), Pitágoras ( famoso pelo seu teorema), Euclides (
que criou a geometria euclidiana). Sendo eles os primeiros geómetras.
A partir do século XIX, surgem várias geometrias não-euclidianas, inventadas
por Gauss, Bolyai e Lobachevski.

7. Geometria plana
A geometria plana, também chamada
geometria elementar ou Euclidiana, teve
início na Grécia antiga. Esse estudo
analisava as diferentes formas de
objetos, e baseia-se em três conceitos
básicos: ponto, reta e plano.

8. O termo axioma é originado da palavra
grega αξιωμα (axioma), que significa
algo que é considerado ajustado ou
adequado, ou que tem um significado
evidente. Entre os filósofos dos gregos
antigos, um axioma era uma
reivindicação que podia ser vista para
ser verdade sem nenhuma necessidade
de prova.
Axioma

9. Geometria espacial
Ramo da geometria que estuda a
medida do espaço ocupado por um
sólido. Cálculo dos volumes de um cubo,
prisma, pirâmide, cone, cilindro, esfera e
de um paralelepípedo.

10. Geometria Escolar
Geometria Euclidiana, recebe este nome por
que Euclides (300 a. C.) foi o primeiro a
sistematizá-la de forma organizada.

11. Problematizações
Por que ensinamos primeiro a geometria plana na escola?

12. Geometria na vida

13. E a Geometria do Pescador, da Costureira etc?
GEOMETRIAS...

14. Triângulo
• O que significa ser uma figura rígida?
• Vamos comprovar!
• Construir a representação de um triângulo e de um de
quadrilátero com canudinhos, sem cortar.
• O que vocês observam quando movimentam os lados
dessas formas geométricas?

15. Refletindo...
Em todo triângulo a soma de dois lados
tem que ser maior que o terceiro.

16. Conhecimento Espacial
Criança
topológico
projetista
euclidiano

17. ELEMENTOS DE UM SÓLIDO GEOMÉTRICO
Vértice
Face
Aresta

18. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
CLASSIFICAÇÃO DOS SÓLIDOS
1
2
3
4
5
6
7

19. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
CLASSIFICAÇÃO DOS SÓLIDOS GEOMÉTRICOS
1. POLIEDROS
2. CORPOS REDONDOS

20. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
•O QUE SÃO POLIEDROS?
Sólidos geométricos que têm todas as faces
planas.
POLI - muitas
EDRO- faces

21. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
CLASSIFICAÇÃO DOS POLIEDROS
•PRISMAS- grupo dos poliedros caracterizado por ter na maioria das
faces (e às vezes em todas) polígonos de quatro lados. As faces opostas
são iguais.

22. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
•PIRÂMIDES- São todos os poliedros cujas as faces laterais
são triangulares e se encontram em um único ponto (o vértice da
pirâmide)
CLASSIFICAÇÃO DOS POLIEDROS

23. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
CLASSIFICAÇÃO DOS POLIEDROS
•OUTROS POLIEDROS- aqueles que não são prismas e nem
pirâmides, são designados simplesmente pelo número de faces que
possui
Dodecaedro regular

24. LABORATÓRIO DE
PESQUIA MULTIMEIOS/
DISCIPLINA ENSINO DE
ELEMENTOS DE UM POLIEDRO
Vértice
Face
Aresta

25. RELAÇÃO DE EULER
V + F = A + 2
Vértice Face Aresta
•Desafio

26. Exemplo 1
Determine o número de faces de um sólido que possui 10 arestas e 6 vértices.
Resolução:
V – A + F = 2
6 – 10 + F = 2
–4 + F = 2
F = 4 + 2
F = 6 Portanto, o sólido possui 6 faces.

27. São figuras fechadas formadas por segmentos de reta, sendo
caracterizados pelos seguintes elementos: ângulos, vértices, diagonais e
lados. De acordo com o número de lados a figura é nomeada.
Polígonos

28. O TANGRAM
Usando o tangram que receberam represente
duas das figuras seguintes:

29. Visualizando as peças fica fácil, já quando vemos a
figura sem visualizar as peças teremos um desafio.
Agora, represente uma das figuras seguintes:

30. Para concluir a atividade discuta com
seu grupo quais outras atividades
podem ser realizadas com o Tangram.
Explore as noções da Geometria
Topológica.

31. Educação do Olhar
• A Geometria procura enfatizar a
importância do olhar e da visualização
na aquisição do conhecimento em
matemática. As reflexões, as
atividades e as discussões propostas
pretendem propiciar um modo de ver
a imagem além do olhar.

32. MATEMÁTICA E ARTE
• São duas disciplinas presentes no
currículo escolar da Educação Básica
que além de estimularem a
sensibilidade, a percepção, a
intuição, a imaginação, contribuem
para a construção de conceitos como:
simetria, razão, proporção,
equilíbrio, repetição, regularidade,
continuidade, entre outros.

33. Exemplo ...
Você conhece a logomarca
da Empresa automobilística
Renault?
Faça a
representação da
imagem.

34. Ver além do olhar...

35. Discussão
• O que você vê? O que você lê?
• Que leitura você faz a partir dessa
imagem?
• Que elementos matemáticos é
possível explorar a partir dessa
imagem?

36. Algumas observações...
• Quando “olho” a imagem vejo o todo e
posso dar uma resposta rápida a partir
do meu referencial;
• Se o aluno só conhece o “losango” ele
não perceberá a tridimensionalidade
da figura;
• Educar o olhar exige adquirir
conhecimentos (instigar o aluno a
ver).

37. Construir a faixa de Möbius
• Pegue uma tira de papel retangular;
• Antes de colar as bodas, dê uma
pequena torção na faixa 180º.

38. • A faixa de Moebius é um tipo
especial de superfície onde não
há lado de dentro ou de fora, ou
seja, nela só há um lado e uma
única borda que é uma curva
fechada. A tal faixa foi descoberta
pelo astrônomo e matemático
alemão August Ferdinand Moebius
(1790-1868).

39. • Em termos matemáticos a faixa de
Möbius é definida como uma
superfície não-orientável
• Seu estudo deu origem a um ramo da
Matemática que chamamos de
Topologia.
A Topologia estuda os espaços
topológicos e é considerada uma
extensão da geometria.

40. O Enigma de Kaspar Hauser
Vídeo
http://www.educadores.diaadia.pr.gov.br/modules/d
ebaser/singlefile.php?id=22258

41. A leitura tanto de textos como de
imagens nas aulas de Matemática
pode ser pensada como uma
prática de ensino.

42. A leitura de uma imagem de acordo
com Pillar (2006, p. 12), pode ser:
a leitura de um texto, de uma
trama, de algo tecido com formas,
cores, texturas, volumes.

43. Leitura e visualização
A importância da leitura e da
visualização, especificamente no ensino
da geometria, é fundamental, pois o
indivíduo passa a ter controle sobre o
conjunto das operações mentais
básicas exigidas no trato da geometria
ao praticar o exercício da visualização
dos objetos geométricos (KALEFF,
2003).

44. (CUNHA, 2009)
Explorando a visualização e a
representação de figuras no espaço
Atividade 1
Quantas caixinhas sobram após encher
completamente a caixa vazia?

45. Forma dentro da forma
(perspectiva)
http://www.educadores.diaadia.pr.gov.br/modules/d
ebaser/singlefile.php?id=9556

46. Livro Matemático - Vídeo
http://www.educadores.diaadia.pr.gov.br/modules/d
ebaser/singlefile.php?id=9567

47. Sugestões de Vídeos
1) Forma que se Transforma
http://www.educadores.diaadia.pr.gov.br/modules/debaser/singl
efile.php?id=9556
2) O Belo
http://www.educadores.diaadia.pr.gov.br/modules/debaser/singl
efile.php?id=9557
3) Escada de Penrose
http://www.educadores.diaadia.pr.gov.br/modules/debaser/singl
efile.php?id=12947

48. A passagem do bidimensional para o
tridimensional
• Tarefa 3 – 20 minutos
• Com 6 quadrados, todos de mesmo tamanho,
obtenham diferentes moldes para se construir
um cubo.
• Quantos moldes diferentes poderemos obter?

49. Mas atenção!
Essas duas figuras representam o mesmo
molde.
Por quê?

50. Aqui estão três moldes
possíveis do cubo.

51. Aqui estão mais três moldes.

52. Outros três...

53. Mais dois moldes, totalizando 11 soluções.

54. Simetria
Para desenvolver a noção se simetria é
importante que:
• complete figuras (igreja, casinha, navio etc.)
usando a simetria;
• encontre o eixo de simetria de algumas
figuras (o uso de espelhos é bastante
recomendado).

55. O papel quadriculado é interessante para obter uma
figura simétrica a uma dada por meio de reflexão em reta.

56. Essa reta pode ser vertical num primeiro
momento.

57. Fazer a reflexão em reta inclinada é mais
difícil...

58. Qual o nome desse polígono?
Tem dois pares de lados paralelos. Seus
quatro lados têm medidas iguais.

59. E desse?
Tem dois pares de lados paralelos.
Seus quatro ângulos são retos.

60. As diagonais do retângulo são eixos de simetria?

61. Enigma de Haberdasher
Uma das criações mais famosas de Dudeney foi sua solução em 1902 para o
Enigma de Haberdasher (cortar um triângulo equilátero e rearranjar as partes
em forma de um quadrado) (haberdasher – loja de armarinhos)

62. Geometria – topológica - 5 anos
Ex: dentro, fora, ao lado, vizinho de etc.
Geometria - projetiva – 7 anos
Ex: antes, depois, primeiro, segundo, à
esquerda, à direita
Aos 9 anos inicia a comparação das figuras
geométricas, relações métricas, aberturas.

63. O desenvolvimento do pensamento
geométrico - a teoria de Van Hiele
Níveis de aprendizagem:
1: Visualização – Os alunos compreendem as figuras
globalmente, isto é, as figuras são entendidas pela sua
aparência;
2: Análise - Os alunos entendem as figuras como o
conjunto das suas propriedades;
3: Ordenação - Os alunos ordenam logicamente as
propriedades das figuras;
4: Dedução - Os alunos entendem a Geometria como
um sistema dedutivo;
5: Rigor - Os alunos estudam diversos sistemas
axiomáticos para a Geometria.

64. Poliedros
Poliedros (poli = muitos; hedros = faces)
são sólidos delimitados por regiões planas
(polígonos) que constituem as denominadas
faces. Os segmentos de reta que limitam as
faces designam-se por arestas e os pontos
de encontro destas por vértices e três
dimensões, sendo elas largura, altura e
comprimento..

65. Poliedros regulares
São chamados de “sólidos
platônicos”, em homenagem ao
filósofo grego Platão (427-347 a.C)
que os utilizava para explicar
cientificamente os fenômenos
naturais. É possível demonstrar que
existem somente cinco poliedros
regulares .

66. DEFINIÇÃO DE POLÍGONOS
Figura plana limitada por segmentos de
reta, chamados lados dos polígonos onde
cada segmento de reta, intersecta
exatamente dois outros extremos; se os
lados forem todos iguais e os ângulos
internos também, o polígono diz-se
regular.

67. Exemplos de alguns polígonos

68. Tetraedro é uma forma espacial,
um poliedro constituído por 4
lados triangulares.
PLANIFICAÇÃO

69. Um hexaedro é um poliedro de 6 faces.
No caso das 6 faces serem iguais e quadradas,
o hexaedro é regular e chama-se cubo.
PLANIFICAÇÃO

70. O octaedro é um
poliedro de oito faces.
PLANIFICAÇÃO

71. Um dodecaedro é um
poliedro de 12 faces.
PLANIFICAÇÃO

72. Um icosaedro é um
poliedro de 20 faces.
PLANIFICAÇÃO

73. Um icosaedro é um
poliedro de 20 faces.
PLANIFICAÇÃO

74. Oficina de poliedros de Platão
http://tele.multimeios.ufc.br/~anaclaudia/
- "Tetraedro"
1 - Passe o cordão por três canudos e forme
uma estrutura rígida (um triângulo)
com um nó.
2 - Passe mais dois canudos pelo cordão
e monte outra estrutura rígida amarrando
no vértice adjacente do triângulo inicial.
3 - Volte o cordão por dentro do canudo a um vértice adjacente.
4 - Passe o último canudo e amarre no vértice livre do
triângulo.
Material Necessário:
- 6 canudos de refrigerante de 12 a 13 cm de
comprimento.
- Cordão (ou linha de crochê) com 1.00 m de comprimento.

75. Oficina de poliedros de Platão
Monte um Hexaedro!
Material Necessário:
- 12 canudos de refrigerante de 12 cm
de comprimento para as arestas e
6 canudos de 20 para as diagonais.
- Cordão (ou linha de crochê) com
4.30 m de comprimento.
Como fazer?
Siga a numeração!
Para iniciar, passe o cordão por três
canudos e forme uma estrutura rígida.
Siga o esquema ao lado.
http://tele.multimeios.ufc.br/~anaclaudia/

76. Oficina de poliedros de
PlatãoOctaedro
Como fazer?
1 - Passe o cordão por três canudos e forme uma estrutura
rígida (um triângulo) com um nó.
2 - Passe mais três canudos pelo cordão e monte outra
estrutura rígida amarrando no vértice do triângulo inicial.
Obtenha uma estrutura com dois triângulos unidos (amarrados)
pelo vértice. Construa outra estrura igual.
3 - Junte as estruturas pegando as bases do triângulo de uma
unindo a um vértice da base em cada triângulo diferente da
outra estrutura.
Obtenha uma estrutura espacial com as duas estruturas unidas.
Material Necessário:
- 12 canudos de refrigerante de 12 a 13 cm de
comprimento.
- Cordão (ou linha de crochê) com 1.50 m de comprimento.
http://tele.multimeios.ufc.br/~anaclaudia/

77. Oficina de poliedros de Platão
Icosaedro Material Necessário:
- 30 canudos de refrigerante de 12 a 13 cm de
comprimento.
- Cordão (ou linha de crochê) com 4.30 m de comprimento.
Como fazer?
Siga a numeração!
Passe o cordão por três canudos e forme uma
estrutura rígida.
Para iniciar, faça a estrutura 1-2-3 de tal forma que as
sobras do cordão fiquem uma grande e outra
pequena. A pequena deve medir o tamanho de quatro
canudos, e a grande será a sobra.
Início 1-2-3-1-nó, 1-6-2-nó, 2-5-6-nó, 6-7-5-nó, 5-8-7-
nó, 7-12-8-nó, 8-9-12-nó, 12-10-9-nó, 9-3-4-2-nó, volte
a linha por 2-5, 5-4-9-nó, volte a linha por 9-8, 8-4-nó,
volte a linha por 4-3, 3-10-nó, 11-12-nó, volte a linha
por 12-7, 7-11-6-nó.
Com a sobra pequena faça a estrutura 1-11-nó, volte a
linha por 11-10, 10-1-nó
http://tele.multimeios.ufc.br/~anaclaudia/

78. Dodecaedro
Oficina de poliedros de
Platão
Oficina de poliedros de
Platão
Material Necessário:
- 20 canudos de
refrigerante de 12 a 13 cm
de comprimento.
- Cordão (ou linha de
crochê) com 3.00 m de
comprimento.

79.  FETISSOV, A. A (2001) demonstração em Geometria. Editora Ulmeiro,
Lisboa.

 FLORES, C. R. (2011). Cultura visual, visualidade, visualização
matemática: balanço provisório, propostas cautelares. Revista
ZETETIKÉ, Campinas: Unicamp – FE - CEMPEM, v.18.

 ZAGO, H. S. (2010). Ensino, Geometria e arte: um olhar para as obras
de Rodrigo de Haro. Florianópolis, SC. 112p. Dissertação defendida
na Universidade Federal de Santa Catarina sob a orientação de
Claudia Flores.

 SOUSA, F. E. E. et al. (2013). Sequência Fedathi: uma Proposta
Pedagógica para o Ensino de Matemática e Ciências. Fortaleza: UFC.