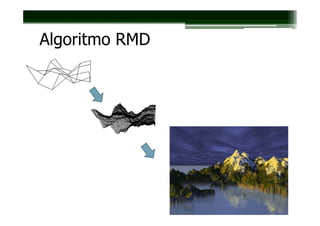
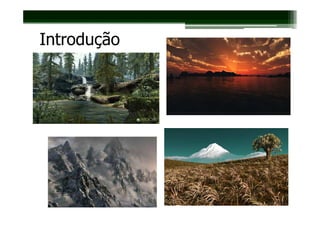
Este documento apresenta uma introdução à geometria fractal e como ela pode ser usada para modelar formas naturais de maneira realista. Ele discute conceitos-chave como auto-similaridade, dimensão fractal e algoritmos como o movimento browniano e RMD que podem gerar fractais. O documento mostra como a geometria fractal captura a irregularidade da natureza e permite que mundos virtuais complexos sejam criados de forma eficiente.

1. Geometria Fractal
Professor Rodrigo Pasti

2. Aula de Hoje
• Fractais
• Geometria Fractal

3. Introdução
• Nos últimos anos houve um grande avanço no
poder de processamento dos sistemas
computacionais.
• Grande parte aos avanços se deve técnicas e
hardwares de computação paralela.
• Este cenário abriu uma vasta possibilidade para
a computação gráfica.
▫ Permitiu criar mundos virtuais inteiros no
computador.
▫ Dentre os quais podemos destacar aqueles que
recriam sistemas naturais completos.

4. Introdução

5. Introdução
• Se vamos recriar mundos naturais então faz-se
necessário entender como é a geometria destes
mundos.
• Representar o mundo natural pode parecer
bastante complexo!
• Como recriar suas formas exatamente como
elas são?
• Existem várias técnicas de Computação Natural
para recriar mundos naturais e veremos
algumas delas na aula de hoje.

6. Introdução
• Desenhar formas naturais requer um
entendimento das “formas” da natureza.
• Um fundamento importante a respeito do
processo de modelagem e síntese de padrões
naturais é considerar que a natureza é fractal.
• Geometria fractal é a base para o
entendimento de fractais.
• De forma simplificada, a geometria fractal pode
ser vista como a geometria da natureza, com
toda a sua irregularidade e estruturas
complexas e fragmentadas.

7. Geometria Fractal

8. Geometria Fractal
• A geometria Euclidiana descreve formas ideais,
como pontos, círculos, retas, esferas,
quadrados, cubos, etc.
• Entretanto, estas formas Euclidianas são
geralmente encontradas apenas em objetos
produzidos por seres humanos.
• A natureza não possui formas suaves e
uniformes e muitos padrões são irregulares e
fragmentados.
• Qual a forma de um floco de neve? E de uma
montanha?

9. Geometria Fractal
• Genericamente, os fractais são caracterizados
por:
▫ Detalhes infinitos;
▫ Comprimento infinito;
▫ Auto-similaridade;
▫ Dimensões fractais;
▫ Ausência de suavidade ou derivadas.
▫ Irregularidades em todas as escalas;

10. Geometria Fractal
• O termo fractal foi cunhado por Mandelbrot
(1983) para identificar uma família de formas
que apresenta padrões irregulares e
fragmentados.
• A geometria fractal é a geometria das formas
irregulares encontradas na natureza.

11. Geometria Fractal

12. Auto-Similaridade

13. Auto-Similaridade
• O conceito de auto-similaridade é essencial
para a geometria fractal.
• O termo auto-similaridade dispensa muitas
explicações.

14. Auto-Similaridade
• O conceito fundamental é que dividindo um
objeto em partes menores, estas se parecem
com a parte maior.
• Repita novamente com as partes menores
obtidas e irá encontrar partes menores ainda e
similares.
• A auto-similaridade se repete então através das
divisões.
• Portanto, a propriedade de auto-similaridade
pode se manter em infinitos estágios.

15. Auto-Similaridade
• Apesar da aparente simplicidade em entender o
conceito por trás da auto-similaridade, uma
definição matemática precisa não é fácil de ser
obtida.
• Alguns objetos podem apresentar:
▫ Auto-similaridade estatística
▫ Auto-similiaridade estrita.
▫ Auto-afinidade.

16. Auto-Similaridade

17. Fractais Pioneiros

18. Fractais Pioneiros
• OS fractais por muito tempo foram considerados
monstros da matemática devido as suas
propriedades não intuitivas.
• O primeiro fractal foi descoberto por K.
Weierstrass em 1861:
▫ Uma função contínua que não é diferenciável em
ponto algum, ou seja, uma curva constituída
somente por “cantos”.
• Outros fractais pioneiros foram descobertos por
G. Cantor, H. von Koch, W. Sierpinski e outros

19. Curva de Koch

20. Curva de Koch
• Propriedades:
• No limite, a curva de Koch não possui segmento algum de
reta; a curva é inteiramente constituída por cantos.
• Portanto a curva não apresenta derivada (tangente) em
ponto algum.
• Embora ela se inicie a partir de uma reta de comprimento
L, seu comprimento é infinito.
• No passo t a curva possui 4t segmentos, cada qual com
comprimento 1/3t
• Portanto, o comprimento total da curva é (4/3)t
• Note que uma curva de comprimento infinito pode ser
colocada em uma área finita.

21. Curva de Koch

22. Curva de Koch

23. Triângulo de Sierpinski

24. Dimensão e Dimensão
Fractal

25. Dimensão Fractal
• Pontos possuem dimensão 0, linhas e curvas
possuem dimensão 1, planos e superfícies
possuem dimensão 2, sólidos possuem
dimensão 3, etc.
• De forma simplificada, um conjunto possui
dimensão d se d variáveis independentes
(coordenadas) são necessárias para descrever
a vizinhança de cada ponto.
• Esta noção de dimensão é denominada de
dimensão topológica.

26. Dimensão Fractal
• Por exemplo, a curva de Koch possui dimensão
topológica 1.
• Mas não pode ser considerada uma curva sob a
perspectiva da geometria euclidiana:
▫ O comprimento entre quaisquer dois pontos da
curva é infinito.
▫ Nenhuma de suas partes é uma linha ou um
plano.
▫ De certa forma, é possível dizer que ela é muito
grande para ser unidimensional e, ao mesmo
tempo, muito pequena para ser bidimensional.
Logo, sua dimensão deve ser um número entre 1
e 2.

27. Dimensão Fractal
• No final do século 19, alguns matemáticos
perceberam que um bom entendimento da
irregularidade ou fragmentação de algumas
formas não pode ser alcançado definindo-se
dimensão como sendo um número de
coordenadas.
• Vamos olhar um cenário parecido em um
problema bem comum.

28. Dimensão Fractal
• Qual o comprimento da costa de um país?

29. Dimensão Fractal
• Este fenômeno foi identificado pelo
meteorologista inglês L. Richardson em 1961
▫ Em sua tentativa de medir o comprimento de
várias costas marítimas.
• Ele percebeu que o comprimento aparente da
costa parecia crescer sempre que o
comprimento do instrumento de medida era
reduzido.
• Isso ocorria, pois quanto menor o comprimento
do medidor maior a amplificação dos detalhes.

30. Dimensão Fractal
• A Richardson concluiu que o comprimento da
costa não é bem definido!
• Propôs uma lei empírica relacionando este
aumento no comprimento da unidade de medida
com a quantidade de detalhes percebidos.
• Logaritmo do comprimento do instrumento de
em função do logaritmo do comprimento total da
costa, produz pontos que tendem a distribuir em
torno de uma linha reta.
• A inclinação da reta resultante o grau de
fragmentação da costa.

31. Dimensão Fractal

32. Dimensão Fractal
• Mandelbrot (1983) encontrou o trabalho de
Richardson e verificou que os fractais poderiam
ser classificados de forma similar.
• E também concluiu que o trabalho dele estava
relacionado com o trabalho de Hausdorff de
1919, a respeito de fractais.
• Com isso cunho os termos fractais e dimensão
fractal para designar objetos que possuem
relação de auto-similiaridade e dimensão não-
inteira.

33. Dimensão Fractal
• O cálculo da dimensão fractal é definido como:
log N
d=
log 1 / m
• Onde N é número de cópias do objeto original e
m é o fator de resolução

34. Dimensão Fractal
• Exemplo: quadrado
m = 1/2 ⇒ N = 4 m = 1/3 ⇒ N = 9
log N log 2 log 9
d= = = =2
log1 / m log 1 /(1 / 2) log1 /(1 / 3)

35. Dimensão Fractal
• Fazendo o mesmo para a curva de Koch
▫ A cada iteração: 4 cópias da linha original com
uma redução de 1/3 de tamanho logo...
log N log 4
d= = = 1.2618
log1 / m log1 /(1 / 3)

36. Dimensão Fractal
• Neste caso, quanto maior a dimensão tendendo
a dois, maior é a complexidade do fractal.
• O espaço Rn possui dimensão fractal n.
• A seguir alguns exemplos de fractais e suas
dimensões respectivas.

37. Sierpinski Triangle
• d = 1,5849

38. Cantor Dust em 3D
• d = 1,8928

39. Greek Cross em 3D
• d = 2,5849

40. Fractais e Aplicações

41. Fractais e Aplicações
• Estamos estudando propriedades de elementos
naturais no espaço.
• Os quais são fundamentados na geometria fractal.
• Estudar a geometria de elementos naturais leva a
várias aplicações:
▫ Entendimento da natureza;
▫ Entendimento e criação de fractais artificiais;
▫ Criação e manutenção de mundos naturais virtuais;
▫ Melhor entendimento de sistemas artificiais que
apresentam características de fractais.
▫ Etc...

42. Fractais e Aplicações
• Peguemos a reprodução de mundos naturais
em mundos artificiais.
• Certos elementos naturais são muito complexos
e possuem muitos detalhes.
• Reproduzir isso em mundos virtuais pode não
ser uma tarefa fácil se pensarmos em reproduzir
parte por parte.
• Imagine os seguintes casos...

43. Fractais e Aplicações

44. Fractais e Aplicações
• Faz sentido desenhar folha por folha?
• Galho por galho?
• Árvore por árvore?
• Cada detalhe da montanha?
• Tudo isso junto?

45. Movimento Browniano

46. Movimento Browniano
• Em 1827 R. Brown observou que pequenas
partículas suspensas em um fluído se
comportam de uma maneira contínua e errática,
• As partículas se movem aleatoriamente porque
o fluído acerta ela em todas as direções.

47. Movimento Browniano
• Através de movimentos brownianos é possível
recriar certos padrões naturais com simples
algoritmos.
• O resultado é a obtenção de fractais que
representam:
▫ Montanhas.
▫ Raios.
▫ Movimento de partículas em líquidos e gases.
▫ Etc...

48. Movimento Browniano
• Uma caminhada aleatória (random walk) é um
caminho que pode ser gerado por um processo
aleatório.
▫ x(t+1) = x(t) + ∆x
▫ y(t+1) = y(t) + ∆
∆y
• onde ∆x e ∆y pode ser distribuições Gaussianas
de média zero e desvio padrão 1.
• Essa caminhada aleatória está intimamente
relacionada com o movimento Browniano.

49. Movimento Browniano

50. Movimento Browniano
• Em uma dimensão, o movimento browniano é
caracterizado por um processo aleatório X(t), que
corresponde a uma função X de uma variável real t
(tempo), cujos valores são variáveis aleatórias X(t1),
X(t2),…
• Em geral é representada por uma distribuição
Gaussiana.
• Um método popular para gerar movimento browniano é
conhecido como algoritmo recursivo da subdivisão
(recursive subdivision algorithm),
▫ Também conhecido como algoritmo do deslocamento
aleatório do ponto médio (random midpoint
displacement algorithm – RMD).

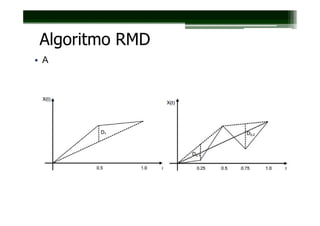
51. Algoritmo RMD
• Se o processo X(t) deve ser computado para o tempo t ∈ [0,
1], então comece definindo X(0) = 0 e escolhendo X(1) como
uma amostra de um valor gaussiano de média 0 e variância
σ2
• No primeiro passo, o ponto médio entre t = 0 e t = 1 é dado
pela média entre X(0) e X(1), mais um desvio D1 de média
zero e variância ∆2 :
▫ ½(X(1) − X(0)) + D1

52. Algoritmo RMD
• A

53. Algoritmo RMD
• Depois de várias iterações

54. Algoritmo RMD
• Mandelbrot e van Ness introduziram em 1968
uma versão de movimento Browniano guiado
por diferenets famílias de gaussianas,
denominaram movimento browniano
fracionário.
• Estes conjuntos de diferentes distribuições
podem ser aplicadas ao algoritmo RMD.
• O que resulta em diferentes comportamentos
para os movimentos, tornando esta versão uma
generalização da anterior.

55. Algoritmo RMD
• Através de diferentes gaussianas obtém-se
diferentes níveis de rugosidade:

56. Algoritmo RMD
• É possível estender o algoritmo RMD para três
ou mais dimensões.

57. Algoritmo RMD
• Sendo possível simular terrenos irregulares e
portanto modelar montanhas e terrenos em
geral.
• A rugosidade do terreno é controlada através de
diferentes gaussianas.

58. Algoritmo RMD

59. Por hoje é só!

60. Referências
• Aulas baseadas em:
▫ Notas de aula do Prof. Fernando Von Zuben
▫ http://www.dca.fee.unicamp.br/~vonzuben/
▫ Notas de aula do Prof. Leandro Nunes de Castro.