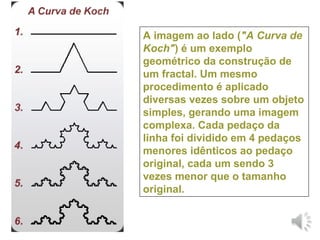
O documento explora a geometria fractal, destacando sua capacidade de descrever fenômenos naturais complexos que não podem ser representados por geometrias tradicionais. Apresenta conceitos como auto-similaridade e complexidade infinita, mencionando o trabalho de Benoît Mandelbrot na investigação de fractais. Também discute a relação entre a medição da costa brasileira e a natureza não-linear das formas geométricas, usando a curva de Koch como exemplo.

2. .

6. .

7. Nuvens não são esferas,
montanhas não são cones,
continentes não são círculos,
o som do latido não é contínuo
e nem o raio viaja em linha
reta."
.

8.  "Fractais são
objetos gerados
pela repetição de
um mesmo
processo
recursivo,
apresentando
auto-semelhança
e complexidade
infinita."
O nascimento do Universo

9. A origem do Universo

10. Anel
de
Areia

15. .
 A Geometria Fractal pode ser utilizada para
descrever diversos fenômenos na natureza,
onde não podem ser utilizadas as
geometrias tradicionais. Nuvens,
montanhas, turbulências, árvores,
crescimento de populações, vasos
sangüíneos e outras formas irregulares
podem ser estudadas e descritas utilizando
as propriedades dos fractais.

16. .

17.  Segundo o velho Euclides, matemático grego que
viveu dois milênios atrás, existem figuras que não
têm dimensão, ou melhor, têm dimensão ZERO. É o
caso dos pontos, como este ponto final (.). Uma
linha, por sua vez - considerada a distância entre
dois pontos quaisquer -, é algo com uma única
dimensão. Já a capa de SUPERINTERESSANTE, de
acordo com a geometria euclidiana, tem duas
dimensões. Pois, para conhecer qual a sua área, é
necessário multiplicar dois números - o do
comprimento pelo da largura. Do mesmo modo, um
bloco possui três dimensões, porque precisamos
multiplicar três números (comprimento, largura e
altura) para saber qual o seu volume. Euclides estava
certo. Mas não resolveu todo o problema.

18. Os contornos das montanhas, a superfície dos
pulmões humanos, a trajetória das gotículas de
água quando penetram na terra - existe uma
infinidade de fenômenos na natureza que não
podem ser descritos por essa geometria toda
certinha. É preciso apelar para complicados
cálculos que resultam nas chamadas
dimensões fracionárias .

19. .
 Complexidade Infinita: É uma propriedade dos
fractais que significa que nunca conseguiremos
representá-los completamente, pois a
quantidade de detalhes é infinita. Sempre
existirão reentrâncias e saliências cada vez
menores.
 Auto-similaridade: Um fractal costuma
apresentar cópias aproximadas de si mesmo em
seu interior. Um pequeno pedaço é similar ao
todo. Visto em diferentes escalas a imagem de
um fractal parece similar

20. .
 Benoît Mandelbrot foi o
pioneiro na investigação da
geometria fractal. No fractal
com o seu nome (Fig.1),
vêem-se pequenos discos
que têm à sua volta outros
pequenos discos, que
também têm à sua volta
outros pequenos discos ainda
mais pequenos, e assim
sucessivamente.

21. .

24. - Joãozinho, qual é o comprimento da costa
brasileira?
- Depende, professor...
- Mas como, Joãozinho, depende do quê?
- Depende do tamanho do meu barco...
- Joãozinho está certo. O comprimento
do litoral depende de como ele é
medido. Isto acontece porque o litoral,
ao contrário do que você lê em muitos
livros de geografia, não é uma linha.

26. A imagem ao lado ("A Curva de
Koch") é um exemplo
geométrico da construção de
um fractal. Um mesmo
procedimento é aplicado
diversas vezes sobre um objeto
simples, gerando uma imagem
complexa. Cada pedaço da
linha foi dividido em 4 pedaços
menores idênticos ao pedaço
original, cada um sendo 3
vezes menor que o tamanho
original.

31. Curva deCurva de
peanopeano