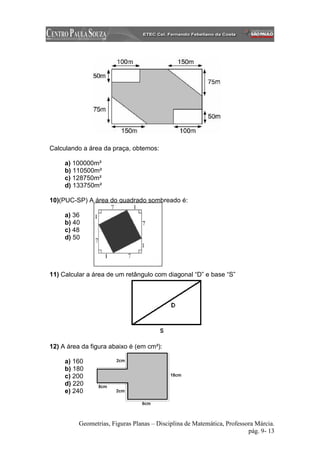
O documento apresenta um trabalho sobre áreas de figuras planas realizado por alunos de uma escola técnica. Ele inclui introdução à geometria, história do desenvolvimento da geometria, cálculo de áreas de diferentes figuras geométricas como retângulos, triângulos e círculos, além de exercícios sobre o tema.