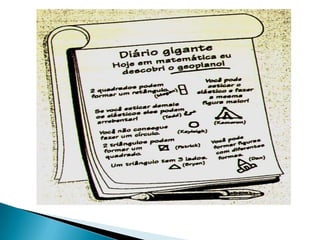
O documento discute como a escrita pode ajudar no ensino de matemática. A escrita promove o pensamento reflexivo, assim como a matemática, ao exigir que os alunos organizem e esclareçam seus pensamentos. A escrita pode ser usada para que os alunos comuniquem suas compreensões, dúvidas e sentimentos sobre matemática. É importante que os alunos tenham um propósito claro para a escrita e saibam para quem estão escrevendo.

1. Alunos: Débora R. P. Barbosa
Elton Ribeiro da Cruz
Laura Apipe

2. Como a escrita pode ajudar
nas aulas de Matemática?

3. O significado;
A qualidade reflexiva;
O valor da escrita em Matemática;

4. “O processo de escrita requer reunir, organizar e
esclarecer pensamentos. Exige descobrir o que você
sabe e o que não sabe. Ela demanda claramente um
pensamento reflexivo. Da mesma forma, o fazer
matemática depende de reunir, organizar e esclarecer
pensamentos, descobrir o que você sabe e o que não
sabe e pensar com clareza. Embora a representação
final de uma busca matemática pareça muito diferente
do produto final de um esforço de escrita, a jornada
mental é, em basicamente, a mesma- atribuir
significado a uma ideia e apresentá-la efetivamente.”
(BURNS, p.3).

5. Comunicação oral;
Comunicação com os pais;
Escrita na fase “durante” lição.

6. Espaço para os estudantes escreverem sobre:
 Sua compreensão conceitual e resolução de
problemas;
 Suas dúvidas em relação ao tópico atual;
 Seus sentimentos sobre aspectos de
matemática.

7. Dicas:
Certifique-se de que o diário seja um lugar
especial.
Pontuar a escrita em diário destrói seu
propósito.
É viável ler e responder cerca de cinco diários
em uma noite.

8. Os estudantes devem ter:
 Um propósito claro e bem definido;
 Saber o que e pra quem escrever;
 Período de tempo para escrever.

9. Assunto: Conceitos e Resolução de
Problemas
 “Eu penso que a resposta é...Eu penso isso
porque...”
 Escreva uma explicação para outros alunos.
 Escreva a um estudante da série X, o que você
aprendeu hoje sobre decimais.

10.  O que foi fácil no trabalho que fizemos hoje? O
que foi difícil? Sobre o que você ainda tem
questões ou dúvidas?
 Você ficou bloqueado hoje ao resolver um
problema? Onde você teve dificuldades lá? Se
você não ficou bloqueado, que ideia lhe ajudou a
resolver o problema?

11.  Depois que você obteve a resposta para o
problema de hoje, o que você fez para se
convencer de que sua resposta estava
correta? Você está seguro de ter obtido a
resposta correta?
 Escreva uma história- problema para essa
figura.

14. É importante que a escrita seja
um registro de algo que o
estudante acabou de fazer e que se
sinta confortável com ela.

17. Tempestade de ideias ou tempestade
cerebral

18. Questionário:
 Perguntas abertas;
 Múltipla escolha (raramente, frequentemente,
às vezes, discordo, não me importo,
concordo)
 Mapas conceituais;
 Desenhos;

19. Lembretes:
 Quão bem você acha que compreendeu o
trabalho que fizemos nos últimos dias sobre
frações?
 Escreva uma coisa que você gostou e uma
coisa que você não gostou sobre a aula de
matemática de hoje

20. Inventário:
( ) SIM
( ) NÃO
( ) TALVEZ

21. Qual deve ser o objetivo de
um teste?

22. Os testes devem refletir as
metas de seu ensino, eles podem
ser elaborados para descobrir que
conceito os estudantes
desenvolveram e como suas ideias
estão conectadas.

23.  Permita as calculadoras o tempo todo;
 Use modelos manipulativos e desenhos;
 Inclua oportunidades para explicações;
 Evite usar “testes pré-respondidos”;

24. Como os professores estão
respondendo às pressões dos
programas de testes estaduais ou
federais instituídos em seu país?

25.  Ensine para o desenvolvimento das ideias
importantes no currículo de matemática;
 Examine as listagens de habilidades e objetivos e
identifique os fundamentos conceituais mais
amplos dos quais eles dependem;
 Certifique-se de que os estudantes tenham uma
oportunidade para aprender o conteúdo nos
Padrões;
 Identifique as ideias mais amplas por trás dos
objetivos

26.  Se os estudantes não desenvolveram os
conceitos, as estratégias de teste serão
completamente inúteis
 O momento adequado para o ensino de
estratégias de teste é logo antes de um teste;

27.  Proporcione experiências com diferentes
formatos de questões;
 Ensine estratégias para fazer testes;
◦ Leia as questões cuidadosamente;
◦ Estime a resposta antes de fazer;
◦ Elimine as opções;
◦ Trabalhe “para trás”;

28. Que ideias vêm à cabeça ao
falar sobre pontuação?

29.  Um grau é uma média de uma série de
pontuações de testes e questionários.
 Acurácia:
técnica computacional para calcular a média
aritmética final

30.  Um grau é uma estatística usada para
comunicar a outros o nível de desempenho
que um estudante atingiu em uma área
particular do conhecimento;
 Acurácia:
informação usada ao preparar o grau +
julgamento do professor + alinhamento das
avaliações com as verdadeiras metas e
objetivos do curso.

31.  O mito da pontuação pela média estatística
de números está tão firmemente incorporado
à escolarização em todos os níveis que você
pode descobrir ser difícil abandoná-lo

32.  É possível reunir informações sobre:
◦ Compreensão;
◦ Processos de resolução de problemas;
◦ Atitudes e convicções;

33.  Decisões difíceis:
◦ Filosóficas;
◦ Aprovação da escola e do município;

34.  Converter quatro em cinco a 80% ou três em
quatro ao grau C pode destruir todo o
propósito de avaliação alternativa e de
rubricas conceituais.
 A avaliação deve ser baseada nas tarefas de
desempenho e em outras atividades para as
quais você estabelece rubricas conceituais;

35.  Os graus que você estabelece devem refletir
todos os seus objetivos;
 Fatores diferentes têm pesos diferentes;
 Um sistema de registro multidimensional é
uma grande auxílio;
 Um espaço para comentários também é útil.

36.  WALLE, John A. Van de; Matemática no
Ensino Fundamental Formação de
Professores e Aplicação em Sala de Aula. 6ª
Ed. Artmed, 2009.