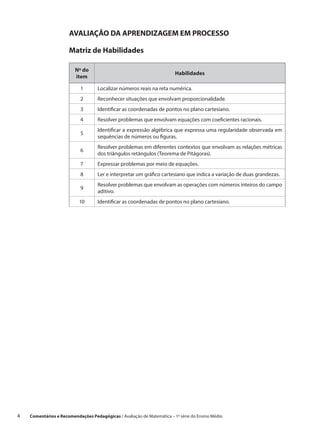
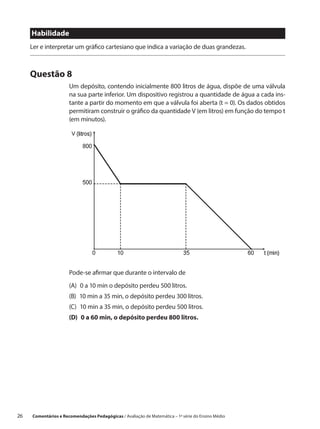
Este documento fornece orientações pedagógicas para professores de matemática da rede estadual de ensino de São Paulo após a aplicação de uma prova de avaliação de aprendizagem. A prova foi aplicada aos alunos do 1o ano do ensino médio e avaliou habilidades como localizar números na reta numérica e identificar coordenadas em um plano cartesiano. O documento explica cada questão, fornece o gabarito correto e sugere atividades de recuperação com base nos erros comuns.