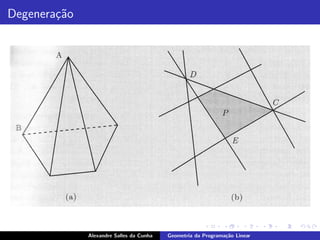
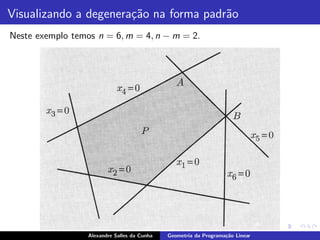
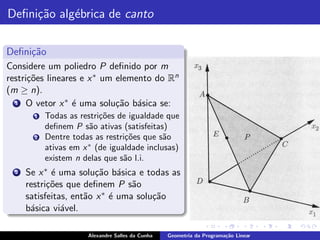
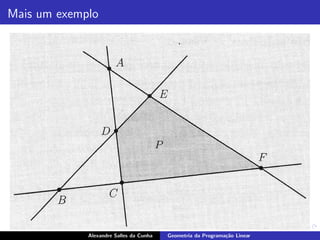
O documento descreve conceitos básicos de geometria da programação linear, incluindo definições de poliedros, semiespaços, hiperplanos e suas relações. Também apresenta definições equivalentes de pontos extremos, vértices e soluções básicas de um poliedro.

1. Geometria da Programa¸˜o Linear
ca
Alexandre Salles da Cunha
DCC-UFMG, Mar¸o 2012 - v.02
c
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

2. Poliedros
Defini¸˜o
ca
Um poliedro ´ um conjunto que pode ser representado da seguinte forma:
e
P = {x ∈ R n : Ax ≥ b}, onde A ´ uma matriz m × n e b ∈ Rm .
e
Poliedro na forma padr˜o
a
Um poliedro ´ dito ser escrito na forma padr˜o se ´ representado da
e a e
seguinte forma: P = {x ∈ R n : Ax = b, x ≥ 0}
Defini¸˜o
ca
Um poliedro limitado ´ chamado politopo.
e
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

3. Semiespa¸os e hiperplanos
c
Defini¸˜o
ca
Seja a um vetor n˜o nulo em Rn e b um escalar.
a
1 O conjunto {x ∈ Rn : a′ x = b ´ chamado hiperplano.
e
2 Os conjuntos {x ∈ Rn : a′ x ≥ b e {x ∈ Rn : a′ x ≤ b s˜o chamados
a
semiespa¸os.
c
Observa¸˜es:
co
O hiperplano ´ a fronteira dos dois semiespa¸os associados.
e c
O vetor a ´ ortogonal a qualquer hiperplano que defina (que depende
e
tamb´m de b).
e
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

4. Poliedros, semiespa¸os, hiperplanos
c
O poliedro pode ser escrito como a interse¸˜o de um n´mero finito de
ca u
restri¸˜es lineares (hiperplanos e semiespa¸os).
co c
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

5. Hiperplanos e conjuntos convexos
Proposi¸˜o
ca
1 Todo poliedro ´ um conjunto convexo.
e
2 A interse¸˜o de conjuntos convexos (poliedros em particular) ´
ca e
convexa.
3 A combina¸˜o convexa de um conjunto finito de elementos de um
ca
conjunto pertence ao conjunto.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

6. Pontos extremos, v´rtices e solu¸˜es b´sicas
e co a
Verificamos atrav´s do m´todo gr´fico de resolu¸˜o que uma solu¸˜o
e e a ca ca
o
´tima de um PL tende a ocorrer em um canto do poliedro que define
a regi˜o de viabilidade do PL.
a
Vamos apresentar trˆs formas alternativas de definir o que venha a ser
e
um canto do poliedro.
◮ Argumentos geom´tricos: pontos extremos e v´rtices de um poliedro.
e e
◮ Argumentos alg´bricos: solu¸oes b´sicas (e b´sicas vi´veis) de um
e c˜ a a a
poliedro.
Mostraremos que estas alternativas s˜o equivalentes.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

7. Ponto extremo
Defini¸˜o
ca
Seja P um poliedro. Um vetor x ∈ P ´ um ponto extremo de P se n˜o for
e a
poss´ escrever x como uma combina¸˜o linear convexa de dois pontos
ıvel ca
z, y ∈ P (distintos de x). Isto ´, n˜o existem z, y ∈ P, z, y = x e
e a
λ ∈ [0, 1] tal que x = λz + (1 − λ)y .
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

8. V´rtice do poliedro
e
Defini¸˜o
ca
Seja P um poliedro. Um vetor x ∈ P ´ um v´rtice de P se existe algum
e e
vetor c ∈ R tal que c ′ x < c ′ y para qualquer y ∈ P, y = x.
Isto ´, x ´ um v´rtice do poliedro se
e e e
{y : c ′ y = c ′ x} ∩ P = {x}.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

9. Desvantagens das descri¸˜es geom´tricas dadas
co e
Estas descri¸˜es n˜o s˜o f´ceis de serem tratadas em um algoritmo.
co a a a
Seria desej´vel dispor de uma descri¸˜o de canto que dependesse da
a ca
representa¸˜o do poliedro em termos de restri¸˜es lineares, que
ca co
pudesse ser resumido a um ”simples”teste alg´brico.
e
Para este prop´sito, vamos considerar a seguinte defini¸ao:
o c˜
Restri¸˜es ativas
co
Assuma que P seja caracterizado por restri¸˜es lineares de igualdade e
co
desigualdade: ai′ x ≥ bi , ∀i ∈ M1 , ai′ x ≤ bi , ∀i ∈ M2 , ai′ x = bi , ∀i ∈ M3 .
Ent˜o se um vetor x ∗ satisfaz ai′ x ∗ = bi para algum i ∈ M1 ∪ M2 ∪ M3
a
dizemos que a restri¸˜o i ´ ativa. Se x ∗ ´ vi´vel, toda restri¸˜o cujo ´
ca e e a ca ındice
i ∈ M3 ´ ativa.
e
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

10. Observa¸˜es
co
Se existem n restri¸˜es ativas em x ∗ , ent˜o x ∗ satisfaz um sistema
co a
linear de n restri¸˜es em n vari´veis. Este sistema linear admite
co a
solu¸˜o unica se estas n restri¸˜es s˜o linearmente independentes (em
ca ´ co a
um abuso de linguagem).
Proposi¸˜o
ca
Dado x ∗ ∈ Rn e I = {i : ai′ x ∗ = bi } o conjunto dos ´
ındices das restri¸˜es
co
ativas em x ∗ . Ent˜o, s˜o equivalentes as afirmativas:
a a
1 Existem n vetores no conjunto {ai : i ∈ I } que s˜o l.i.
a
2 span({ai : i ∈ I }) = Rn
3 O sistema linear ai′ x = bi , ∀i ∈ I possui solu¸˜o unica.
ca ´
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

11. Prova
Prova
(1) ⇔ (2)
(1) ← (2):
Suponha que os vetores ai : i ∈ I gerem Rn . Ent˜o a
dim(span({ai : i ∈ I })) = n e {ai : i ∈ I } formam uma base de Rn ,
sendo linearmente independente.
(1) → (2):
Suponha que os vetores ai : i ∈ I sejam l.i. Ent˜o o subespa¸o gerado
a c
por estes n vetores ´ n dimensional e necessita ser R
e n . Assim
qualquer vetor em Rn pode ser escrito como uma combina¸˜o linear
ca
de ai : i ∈ I
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

12. Prova
(2) ⇔ (3) :
(2) ← (3) : (por contradi¸˜o)
ca
Assuma que o sistema ai′ x = bi : i ∈ I admita duas solu¸˜es distintas
co
x 1 e x 2 . Ent˜o o vetor d = x 1 − x 2 = 0 satisfaz ai d = 0, ∀i ∈ I e n˜o
a a
pode ser escrito como combina¸˜o linear dos vetores ai : i ∈ I e
ca
portanto span({ai : i ∈ I } = Rn (absurdo !). Logo x 1 = x 2 .
(2) → (3) : Se os vetores ai : i ∈ I n˜o geram Rn , existe d = 0 tal
a
que ai′d = 0 : i ∈ I .
Ent˜o se x satisfaz ai′ x = bi : i ∈ I , temos que ai′ (x + d) = bi : i ∈ I e
a
temos m´ltiplas solu¸˜es para o sistema linear.
u co
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

13. Defini¸˜o alg´brica de canto
ca e
Defini¸˜o
ca
Considere um poliedro P definido por m
restri¸˜es lineares e x ∗ um elemento do Rn
co
(m ≥ n).
1 O vetor x ∗ ´ uma solu¸˜o b´sica se:
e ca a
1 Todas as restri¸oes de igualdade que
c˜
definem P s˜o ativas (satisfeitas)
a
2 Dentre todas as restri¸oes que s˜o
c˜ a
ativas em x ∗ (de igualdade inclusas)
existem n delas que s˜o l.i.
a
2 Se x ∗ ´ uma solu¸˜o b´sica e todas as
e ca a
restri¸˜es que definem P s˜o
co a
satisfeitas, ent˜o x ∗ ´ uma solu¸˜o
a e ca
b´sica vi´vel.
a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

14. Caso em que n > m
Se o n´mero m de restri¸˜es lineares empregadas para representar um
u co
poliedro ´ inferior a n, o n´mero de restri¸˜es ativas ´ sempre inferior
e u co e
a n.
Consequentemente, n˜o existem solu¸˜es b´sicas ou b´sicas vi´veis.
a co a a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

15. Observa¸˜es
co
Note na figura anterior que os pontos A, B, C s˜o solu¸˜es b´sicas
a co a
vi´veis.
a
O ponto D n˜o ´ b´sica porque n˜o sastisfaz a restri¸˜o de igualdade
a e a a ca
x1 + x2 + x3 = 1.
Entretanto, se a restri¸˜o x1 + x2 + x3 = 1 for reescrita como
ca
x1 + x2 + x3 ≤ 1 e x1 + x2 + x3 ≥ 1, o ponto D passa a ser solu¸˜o
ca
b´sica da nova forma empregada para representar o poliedro P.
a
Isto ´, o modo como o poliedro ´ representado em termos de
e e
restri¸˜es lineares influencia o conjunto de solu¸oes b´sicas.
co c˜ a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

16. Mais um exemplo
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

17. As trˆs formas de representa¸˜o s˜o equivalentes
e ca a
Teorema
Seja P um poliedro n˜o vazio e x ∗ ∈ P. Ent˜o as seguintes afirmativas
a a
s˜o equivalentes:
a
1 x ∗ ´ um ponto extremo;
e
2 x ∗ ´ um v´rtice;
e e
3 x ∗ ´ uma solu¸˜o b´sica vi´vel.
e ca a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

18. Prova: v´rtice → ponto extremo
e
Sem perda de generalidade, vamos assumir que P seja escrito em termos
de restri¸˜es de igualdade ai′ x = bi e desigualdade na forma ai′ x ≥ bi .
co
Prova
Suponha que x ∗ seja um v´rtice de P. Ent˜o, por defini¸˜o, existe
e a ca
c ∈ Rn tal que c ′ x ∗ < c ′ y para qualquer y ∈ P, y = x.
Ent˜o tome y , z ∈ P distintos de x ∗ e λ ∈ [0, 1].
a
Temos que c ′ x ∗ < c ′ (λy + (1 − λ)z) e consequentemente
x ∗ = λy + (1 − λ)z.
Logo o v´rtice x n˜o pode ser escrito como combina¸˜o convexa de
e a ca
dois outros pontos quaisquer de P e, portanto, o v´rtice ´ tamb´m
e e e
um ponto extremo.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

19. Ponto extremo → solu¸˜o b´sica vi´vel
ca a a
Prova
Vamos supor que x ∗ ´ ponto extremo e n˜o ´ solu¸˜o b´sica vi´vel.
e a e ca a a
Seja I = {i : ai′ x ∗ = bi }. Ent˜o como x ∗ n˜o ´ solu¸˜o b´sica vi´vel,
a a e ca a a
n˜o existem, dentre as restri¸˜es em I , n linearmente independentes.
a co
Portanto, os vetores ai : i ∈ I geram um subespa¸o pr´prio de Rn .
c o
Ent˜o deve haver d ∈ Rn tal que ai′ d = 0, ∀i ∈ I . Dado um ǫ > 0
a
suficientemente pequeno, consideremos os vetores y = x ∗ + ǫd e
z = x ∗ − ǫd. Observe que ai′ y = ai′ z = ai′ x ∗ = bi , ∀i ∈ I . Al´m disto,
e
para i ∈ I temos que ai′ x ∗ > bi .
Se escolhermos ǫ convenientemente (tal que
ǫ|ai′ d| < ai′ x ∗ − bi , ∀i ∈ I ), temos que y ∈ P. Por argumento similar,
mostramos que z ∈ P. Ent˜o, x ∗ = z+y e x ∗ n˜o pode ser ponto
a 2 a
extremo (contradi¸˜o !).ca
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

20. Solu¸˜o b´sica vi´vel → v´rtice
ca a a e
Prova
Considere que x ∗ ´ uma solu¸˜o b´sica vi´vel e I = {i : ai′ x ∗ = bi }.
e ca a a
Seja c = i ∈I ai . Ent˜o temos c
a ′x ∗ = ′ ∗
i ∈I ai x = i ∈I bi . Por
outro lado, para qualquer x ∈ P temos c ′x = ai′ x ≥ i ∈I bi .
i ∈I
Consequentemente, mostramos que x ∗ resolve o PL cuja fun¸˜o
ca
objetivo ´ (min) c e regi˜o de viabilidade ´ P.
e a e
O m´ ınimo de c ′ x ∗ = i ∈I ai′ x ∗ = i ∈I bi ocorre quando
′ x = b , ∀i ∈ I .
ai i
Como x ∗ ´ uma solu¸˜o b´sica vi´vel, existem n restri¸˜es l.i. ativas
e ca a a co
em x ∗ (dentre aquelas que definem I ) e x ∗ ´ a solu¸˜o unica deste
e ca ´
sistema linear.
Portanto, x ∗ ´ o unico minimizador de c ′ x sobre P e, portanto, ´ um
e ´ e
v´rtice de P.
e
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

21. Observa¸˜es
co
Corol´rio
a
Dado um n´mero finito de restri¸˜es de desigualdades que definem um
u co
poliedro, s´ pode haver um n´mero finito de solu¸˜es b´sicas ou b´sicas
o u co a a
vi´veis associadas a P.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

22. Solu¸˜es b´sicas adjacentes
co a
Duas solu¸˜es b´sicas para um conjunto de restri¸˜es lineares em Rn
co a co
s˜o adjacantes se podemos encontrar n − 1 restri¸˜es linearmente
a co
independentes ativas que s˜o comuns `s duas solu¸˜es.
a a co
Se duas solu¸˜es b´sicas adjacentes s˜o tamb´m vi´veis, o segmento
co a a e a
de reta que as une ´ chamado aresta do conjunto de viabilidade.
e
Na figura abaixo, D e E s˜o adjacentes a B. A e C s˜o adjacentes a D.
a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

23. Poliedros na forma padr˜o
a
At´ o momento, a defini¸˜o de solu¸˜o b´sica foi dada para um
e ca ca a
poliedro descrito de forma geral.
Vamos especializar esta defini¸˜o para a forma padr˜o, do tipo
ca a
P = {x ∈ Rn : Ax = b, x ≥ 0}.
A especializa¸˜o ser´ fundamental para o desenvolvimento do M´todo
ca a e
Simplex.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

24. Hip´teses iniciais
o
Consideremos P = {x ∈ Rn : Ax = b, x ≥ 0}, onde a matriz A possui m
linhas.
Vamos assumir que as m linhas de A s˜o linearmente independentes.
a
Futuramente, mostraremos que se houver alguma linha linearmente
dependente, esta pode ser eliminada, sem descaracteriza¸˜o da regi˜o
ca a
de viabilidade (isto ´, a linha ´ redundante).
e e
Como as linhas de A s˜o n dimensionais, isto implica que m ≤ n.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

25. Solu¸˜es b´sicas
co a
Pela defini¸˜o dada anteriormente, uma solu¸˜o b´sica para
ca ca a
P = {x ∈ Rn : Ax = b, x ≥ 0} deve ser tal que:
As m linhas que definem Ax = b s˜o ativas (satisfeitas).
a
Como estas m linhas s˜o l.i., ´ necess´rio escolher dentre as demais
a e a
restri¸˜s xi ≥ 0, n − m para serem ativas.
ce
Estas restri¸˜es de n˜o negatividade n˜o podem ser quaisquer.
co a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

26. Solu¸˜es b´sicas na forma padr˜o
co a a
Teorema
Considere as restri¸˜es Ax = b e x ≥ 0 e assuma que a matriz A, m × n,
co
possua m linhas linearmente independentes.
Um vetor x ∈ Rn ´ uma solu¸˜o b´sica se e somente se Ax = b e existirem
e ca a
´
ındices B(1), . . . , B(m) de colunas de A tais que:
1 As colunas AB(1) , AB(2) , . . . , AB(m) s˜o linearmente independentes;
a
2 Se i ∈ {B(1), . . . , B(m)} ent˜o xi = 0.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

27. Prova: Se (1) e (2) → ´ sol. b´sica
e a
Prova
Considere x ∈ Rn e assuma que existam ´
ındices B(1), . . . , B(m)
satisfazendo (1) e (2) acima.
As restri¸˜es ativas xi = 0 para os ´
co ındices i ∈ {B(1), . . . , B(m)}, em
conjunto com Ax = b, garante que
m n
i =1 AB(i ) xB(i ) = i =1 Ai xi = Ax = b.
Como as colunas B(1), . . . , B(m) s˜o l.i., o sistema linear formado
a
pelas restri¸˜es ativas possui solu¸˜o unica.
co ca ´
Ou seja, existem n restri¸˜es ativas linearmente independentes, e
co
ent˜o x ´ uma solu¸˜o b´sica (segundo a equivalˆncia das defini¸˜es
a e ca a e co
anteriores).
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

28. Prova: Se ´ sol. b´sica → (1) e (2)
e a
Parte 1
Prova
Assuma que x ´ uma sol. b´sica. Vamos mostrar que (1) e (2) s˜o
e a a
ent˜o satisfeitas.
a
Seja xB(1) , . . . , xB(k) as componentes de x que s˜o n˜o nulas.
a a
Uma vez que x ´ b´sica, o sistema de restri¸˜es ativas formado por
e a co
Ax = b e xi = 0, i ∈ {B(1), . . . , B(k)} admite sol. unica.
´
Equivalentemente o sistema k=1 AB(i ) xB(i ) = b admite solu¸˜o
i ca
unica.
´
Ou seja, as colunas B(1), . . . , B(k) s˜o li e ent˜o k ≤ m.
a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

29. Prova: Se ´ sol. b´sica → (1) e (2)
e a
Mostramos at´ agora que B(1), . . . , B(k) s˜o li e k ≤ m.
e a
Parte 2
Prova
Uma vez que o posto de A ´ m, A possui m linhas e colunas li.
e
Ent˜o ´ poss´ escolher outras m − k colunas B(k + 1), . . . , B(m)
a e ıvel
de A, de forma que as colunas B(1), . . . , B(m) sejam li.
Observe ent˜o que se i ∈ {B(1), . . . , B(m)} ent˜o xi = 0,
a a
completando a prova.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

30. Um procedimento para obten¸˜o de solu¸˜es b´sicas
ca co a
1 Escolha m colunas AB(1) , . . . , AB(m) linearmente independentes de A.
2 Fa¸a xi = 0, ∀i ∈ {B(1), B(2), . . . , B(m)}.
c
3 Resolva o sistema linear de m restri¸˜es Ax = b para as vari´veis
co a
xB(1) , xB(2) , . . . , xB(m) .
Se as solu¸˜es geradas atrav´s do procedimento acima satisfizerem
co e
xi ≥ 0, ∀i ∈ {B(1), . . . , B(m)}, a solu¸˜o ´ chamada b´sica vi´vel.
ca e a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

31. Nomenclatura
As colunas B(1), . . . , B(m) s˜o denominadas b´sicas, assim como as
a a
vari´veis de decis˜o a elas associadas.
a a
As demais colunas (e vari´veis) s˜o denominadas n˜o b´sicas.
a a a a
A matriz B (m × m) formada pelas colunas b´sicas,
a
B = [AB(1) AB(2) · · · AB(m) ], ´ chamada base.
e
As vari´veis b´sicas xB s˜o obtidas resolvendo-se o sistema linear:
a a a
xB = B −1 b.
Se xB ≥ 0, x ´ uma solu¸˜o b´sica vi´vel.
e ca a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

32. Exemplo
   
1 1 2 1 0 0 0 8
 0 1 6 0 1 0 0 
  12 

 1 x = 
0 0 0 0 1 0   4 
0 1 0 0 0 0 1 6
Se escolhermos A4 , A5 , A6 , A7 como colunas b´sicas, temos que B
a
corresponde ` uma matriz n˜o singular e xB = (0, 0, 0, 8, 12, 4, 6) ≥ 0
a a
´ uma solu¸˜o b´sica vi´vel.
e ca a a
Outra base pode ser obtida escolhendo-se como b´sicas as colunas
a
A3 , A5 , A6 , A7 . A matriz B resultante ´ claramente n˜o singular e a
e a
solu¸˜o b´sica xB = (0, 0, 4, 0, −12, 4, 6) ≥ 0 ´ n˜o vi´vel.
ca a e a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

33. Interpreta¸˜o econˆmica das solu¸˜es b´sicas
ca o co a
Uma solu¸˜o b´sica permite sintetizar b ∈ Rm usando-se apeans m
ca a
recursos, isto ´, b = m AB(i ) xB(i ) .
e i =1
Em uma solu¸˜o b´sica vi´vel, a s´
ca a a ıntese ocorrer por meio de pesos
n˜o negativos das colunas b´sicas (xB ≥ 0).
a a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

34. Correspondˆncia entre bases e solu¸˜es b´sicas
e co a
Diferentes solu¸˜es b´sicas precisam corresponder a diferentes bases,
co a
uma vez que uma base determina unicamente uma solu¸˜o b´sica.
ca a
Entretanto, duas bases diferentes podem levar ` mesma solu¸˜o
a ca
b´sica.
a
Este fenˆmeno possui consequˆncias muito importantes do ponto de
o e
vista algoritmico.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

35. Bases adjacentes e solu¸˜es b´sicas adjacentes
co a
Da mesma forma que definimos solu¸˜es b´sicas adjacentes como aquelas
co a
que compartilham n − 1 restri¸˜es l.i. justas, definimos bases adjacentes
co
matrizes que compartilham m − 1 colunas (isto ´, que diferem apenas por
e
uma coluna).
 
1 1 2 1 0 0 0
 0 1 6 0 1 0 0 
 
 1 0 0 0 0 1 0 
0 1 0 0 0 0 1
{A4 , A5 , A6 , A7 } e {A3 , A5 , A6 , A7 } s˜o bases adjacentes.
a
As correspondentes solu¸˜es b´sicas (0, 0, 0, 8, 12, 4, 6) e
co a
(0, 0, 4, 0, −12, 4, 6) s˜o adjacentes uma vez que n = 7 e temos que
a
as restri¸˜es x1 ≥ 0, x2 ≥ 0 em conjunto com as restri¸˜es de
co co
igualdade formam um sistema de 6 restri¸˜es justas l.i.
co
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

36. A hip´tese de posto completo de A
o
Teorema
Seja P = {x ∈ Rn : Ax = b, x ≥ 0} um poliedro n˜o vazio, onde
a
A∈R m×n possui linhas a′ , a′ , . . . , a′ .
1 2 m
Assuma que o posto de A seja k < m e que as primeiras k linhas de A,
′ ′ ′
a1 , a2 , . . . , ak , sejam l.i.
Ent˜o o poliedro
a
Q = {x ∈ Rn : ai′ x = bi , ∀i = 1, . . . , k, ≥ 0}
e P s˜o idˆnticos (P = Q) e n˜o h´ perda de generalidade na hip´tese de
a e a a o
posto completo de A.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

37. Prova
Prova
Observe que se as primeiras k linhas n˜o forem l.i. podemos
a
rearranjar a ordem das linhas de forma que isto aconte¸a.
c
Claramente P ⊂ Q.
Vamos mostrar que Q ⊂ P e ent˜o P = Q.
a
Se o posto de A ´ k, ent˜o o espa¸o linha de A possui dimens˜o k e
e a c a
qualquer linha de A pode ser escrita como combina¸˜o linear destas k
ca
linhas, isto ´, ai′ = k λij aj′ para escalares λij .
e j=1
Considere x ∈ P. Observe que ai′ x = bi , ∀i = 1, . . . , m. Logo
bi = ai′ x = k λij aj′ x = k λij bj , ∀i = 1, . . . , m
j=1 j=1
k k
Tome agora y ∈ Q. Ent˜o ai′ y =
a ′
j=1 λij aj y = j=1 λij bj = bi .
Logo y ∈ P e Q ⊂ P.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

38. Degenera¸˜o
ca
De acordo com a nossa defini¸˜o, em uma solu¸ao b´sica, dispomos
ca c˜ a
de n restri¸˜es ativas linearmente independentes.
co
Obviamente, o m´ximo n´mero de restri¸˜es linearmente
a u co
independentes ´ n, mas podemos ter em uma solu¸˜o b´sica mais de
e ca a
n restri¸˜es ativas.
co
Defini¸˜o
ca
Uma solu¸˜o b´sica x ∈ Rn ´ chamada degenerada se mais de n restri¸˜es
ca a e co
s˜o ativas em x.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

39. Degenera¸˜o - Exemplo
ca
Considere o politopo P dado pelas restri¸˜es:
co
x1 + x2 + 2x3 ≤ 8
x2 + 6x3 ≤ 12
x1 ≤ 4
x2 ≤ 6
x1 , x2 , x3 ≥ 0.
(2, 6, 0) n˜o degenerada, uma vez que h´ exatamente trˆs restri¸˜es
a a e co
ativas no ponto (s˜o justas: x3 = 0, x2 ≤ 6, x1 + x2 + 2x3 ≤ 8)
a
(4, 0, 2) ´ uma solu¸˜o degenerada (s˜o justas:
e ca a
x1 + x2 + 2x3 ≤ 8, x2 + 6x3 ≤ 12, x1 ≤ 4, x2 ≥ 0).
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

40. Degenera¸˜o
ca
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

41. Degenera¸˜o no formato padr˜o
ca a
Em uma solu¸˜o b´sica de um poliedro na forma padr˜o, as m
ca a a
restri¸˜es de igualdade s˜o ativas.
co a
Assim sendo, ter mais que n desigualdades ativas em um ponto,
equivale a ter mais de n − m vari´veis no n´ zero.
a ıvel
Defini¸˜o
ca
Considere o poliedro na forma padr˜o P = {x ∈ Rn : Ax = b, x ≥ 0}.
a
Assuma que x seja uma solu¸˜o b´sica ´ uma solu¸˜o b´sica e que m seja
ca a e ca a
o n´mero de linhas de A. O vetor x ´ chamado degenerado se mais de
u e
n − m componentes do vetor x s˜o nulas.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

42. Exemplo
Consideremos o poliedro do exemplo anterior, ap´s introdu¸˜o de vari´veis
o ca a
de folga.    
1 1 2 1 0 0 0 8
 0 1 6 0 1 0 0   12 
A=  1
b =  
0 0 0 0 1 0   4 
0 1 0 0 0 0 1 6
Vamos considerar a solu¸˜o b´sica associada `s colunas
ca a a
A1 , A2 , A3 , A7.
Fixando x4 = x5 = x6 = 0 e resolvendo linear BxB = b, temos que
x = (4, 0, 2, 0, 0, 0, 6) que ´ uma solu¸˜o b´sica (vi´vel) degenerada,
e ca a a
uma vez que x2 = 0 ´ uma vari´vel b´sica em 0.
e a a
Consequentemente, temos 4 vari´veis no n´ zero e n˜o
a ıvel a
n − m = 7 − 4 = 3 apenas.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

43. Interpretando a degenera¸˜o
ca
Escolhemos uma solu¸˜o b´sica selecionando n restri¸˜es linearmente
ca a co
independentes para serem satisfeitas na igualdade. Percebemos em
seguida que outras restri¸˜es, al´m das n que selecionamos, s˜o
co e a
tamb´m justas naquela solu¸˜o b´sica.
e ca a
Se as entradas de A e b forem escolhidas aleatoriamente, a chance
das solu¸˜es b´sicas decorrentes serem degeneradas ´ muito pequena.
co a e
Em muitas aplica¸˜es (onde A e b possui estrutura n˜o aleat´ria), a
co a o
degenera¸˜o ´ bastante comum.
ca e
A figura abaixo procura ilustrar que pequenas perturba¸˜es nos dados
co
do Programa Linear permitem eliminar a degenera¸˜o.
ca
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

44. Visualizando a degenera¸˜o na forma padr˜o
ca a
Neste exemplo temos n = 6, m = 4, n − m = 2.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

45. A degenera¸˜o n˜o ´ uma propriedade puramente
ca a e
geom´trica
e
A degenera¸˜o n˜o ´ independente do modo como representamos o
ca a e
poliedro. Considere o poliedro P representado de duas formas:
P = {x ∈ R3 : x1 − x2 =
0, x1 + x2 + 2x3 = 2, x1 ≥
0, x2 ≥ 0, x3 ≥ 0 e
P = {x ∈ R3 : x1 − x2 =
0, x1 + x2 + 2x3 = 2, x1 ≥
0, x3 ≥ 0.
O ponto x = (0, 0, 1) ´
e
degenerado diante da primeira
representa¸˜o, e n˜o degenerado
ca a
diante da segunda.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

46. Outro exemplo
Considere uma solu¸˜o x ∗ b´sica vi´vel n˜o degenerada para um
ca a a a
poliedro na forma padr˜o P = {x ∈ R
a n : Ax = b, x ≥ 0}, onde
A ∈ Rm×n . Temos ent˜o exatamente n − m vari´veis satisfazendo
a a
∗ = 0.
xi
Se reescrevermos o poliedro da seguinte forma
P = {x ∈ Rn : Ax ≥ b, −Ax ≥ −b, x ≥ 0} temos exatamente as
mesmas n − m vari´veis satisfazendo xi∗ = 0 e mais 2m restri¸˜es
a co
justas em x ∗ (totalizando n + m justas). Portanto, para esta nova
representa¸˜o, x ∗ ´ uma solu¸˜o b´sica vi´vel degenerada.
ca e ca a a
Mostramos casos onde uma solu¸˜o ´ degenerada diante de uma
ca e
representa¸˜o e n˜o ´ diante de outra.
ca a e
´ poss˜ mostrar que se uma solu¸˜o b´sica ´ degenerada diante de
E ivel ca a e
uma forma padr˜o particular, ent˜o ser´ degenerada diante de
a a a
qualquer outra forma padr˜o do mesmo poliedro.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

47. Existˆncia de pontos extremos
e
Vamos obter uma condi¸˜o suficiente para um poliedro possuir um
ca
ponto extremo.
Nem todo poliedro possui um ponto extremo. Exemplo: um
semiespa¸o em Rn (n > 1) n˜o possui ponto extremo.
c a
O poliedro P = {x ∈ R n : Ax ≥ b} onde A ∈ Rm×n e m < n n˜oa
possui ponto extremo.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

48. Existˆncia de pontos extremos
e
Defini¸˜o
ca
Um poliedro P ⊂ Rn possui uma linha se existir um vetor x ∈ P e uma
dire¸˜o d ∈ Rn n˜o nula tal que x + λd ∈ P para todo λ.
ca a
Teorema
Suponha que o poliedro P = {x ∈ Rn : ai′ x ≥ bi , i = 1, . . . , m} ´ n˜o
e a
vazio. Ent˜o, as seguintes afirmativas s˜o equivalentes:
a a
1 O poliedro P possui pelo menos um ponto extremo.
2 O poliedro P n˜o possui uma linha.
a
3 Dentre os vetores ai : i = 1, . . . , m, existem n linearmente
independentes.
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

49. Prova
Prova
(2) → (1)
Seja x ∈ P e I = {i : ai′ x = bi }. Se n dos vetores em I s˜o l.i. nada
a
temos a provar (x seria, por defini¸˜o uma solu¸` b´sica). Ent˜o
ca c.ao a a
assumimos n˜o ser este o caso.
a
Ent˜o os vetores em I formam um subespa¸o pr´prio de Rn , existindo
a c o
portanto d ∈ Rn tal que ai′ d = 0, i ∈ I .
Consideremos os pontos da forma y = x + λd. Para todo i ∈ I ,
temos ai′ y = ai′ x + λai′ d = ai′ x = bi .
Como n˜o h´ uma linha e como ao longo de d todas as restri¸˜es em
a a co
I permanecem ativas, h´ um valor para λ, digamos λ∗ , para o qual
a
uma nova restri¸˜o se torna justa. Isto ´, existe
ca e
λ∗ : aj′ (x + λ∗ d) = bj , j ∈ I .
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

50. Prova
Prova
(2) → (1) - Continua¸˜o
ca
Afirmamos que aj n˜o ´ uma combina¸˜o linear dos vetores ai : i ∈ I .
a e ca
′ x = b e a′ (x + λd) = b . Logo a′ d = 0.
Isto porque aj j j j j
Recorde que d ⊥ span({ai : i ∈ I }), logo ai′ d = 0.
Uma vez que aj n˜o ´ ortogonal a d e ai : i ∈ I s˜o ortogonais a d, aj
a e a
n˜o pode ser uma combina¸˜o linear dos vetores ai : i ∈ I .
a ca
Logo, o n´mero de restri¸˜es l.i. aumentou em uma unidade ao
u co
movermos de x para x + λ∗ d.
Repetindo o processo quantas vezes forem necess´rias, terminamos
a
em um ponto em que o n´mero de restri¸˜es l.i. ´ n e, por defini¸˜o,
u co e ca
este ponto ´ uma solu¸˜o b´sica.
e ca a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

51. Prova
Prova
(1) → (3)
Se P possui um ponto extremo x, ent˜o x ´ uma solu¸˜o b´sica
a e ca a
vi´vel.
a
Por defini¸˜o, existem para x, n restri¸˜es ativas em x cujos vetores
ca co
ai s˜o l.i.
a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

52. Prova
Prova
(3) → (2)
Assuma que n dos vetores ai , digamos, a1 , . . . , an , sejam l.i.
Suponha que P contenha uma linha x + λd, onde d ´ um vetor n˜o
e a
nulo.
Ent˜o temos ai′ (x + λd) ≥ bi , ∀i , ∀λ ∈ R. Para que isto ocorra,
a
ai′ d = 0 (se ai′ d < 0, tomar´
ıamos λ suficientemente grande e
violariamos a restri¸˜o. Racioc´ an´logo vale se ai′ d > 0.)
ca ınio a
Entretanto, como os vetores a1 , . . . , an s˜o l.i., temos que d = 0.
a
Logo, temos uma contradi¸˜o e P n˜o pode conter uma linha.
ca a
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca

53. Otimalidade de pontos extremos
Na medida em que um Programa Linear possui uma solu¸˜o ´tima e
ca o
na medida em que o conjunto de pontos vi´veis de um PL inclui pelo
a
menos um ponto extremo, ent˜o podemos sempre encontrar uma
a
solu¸˜o ´tima no conjunto de pontos extremos.
ca o
Teorema
Considere o Programa Linear que consiste em minimizar c ′ x em um
poliedro P. Assuma que P possui pelo menos um ponto extremo e que
exista uma solu¸˜o ´tima para o Programa Linear. Ent˜o, existe uma
ca o a
solu¸˜o ´tima que ´ um ponto extremo de P.
ca o e
Teorema
Considere o Programa Linear que consiste em minimizar c ′ x em um
poliedro P. Assuma que P possui pelo menos um ponto extremo. Ent˜o,
a
ou o custo ´timo ´ −∞ ou existe um ponto extremo de P que ´ ´timo.
o e eo
Alexandre Salles da Cunha Geometria da Programa¸˜o Linear
ca