Este documento apresenta um guia sobre como utilizar o software Geogebra para construir figuras geométricas planas. Ele contém instruções sobre as ferramentas do Geogebra e sugere seis atividades com exemplos de construções de figuras como retângulos, triângulos, polígonos e pontos notáveis do triângulo. O documento visa auxiliar professores a incorporarem o Geogebra em suas aulas de geometria.

















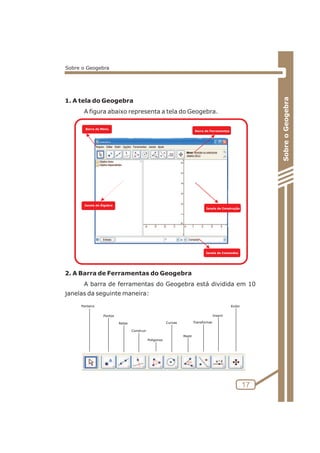













































































![ATIVIDADE 5: PONTOS NOTÁVEIS DO TRIÃNGULO
105
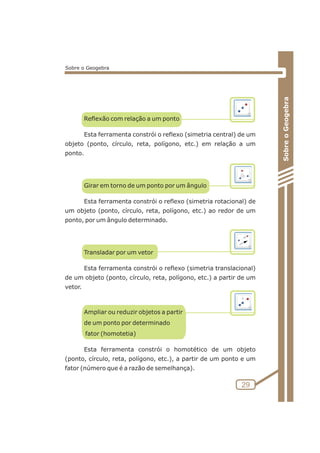
Atividade 5: Pontos notáveis do triângulo
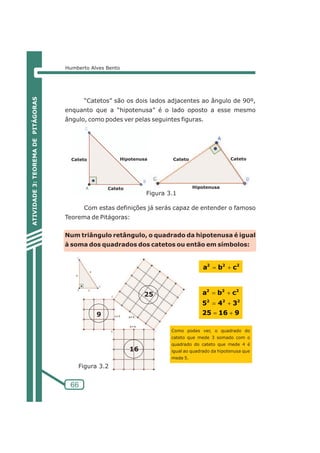
Figura 5.2.1
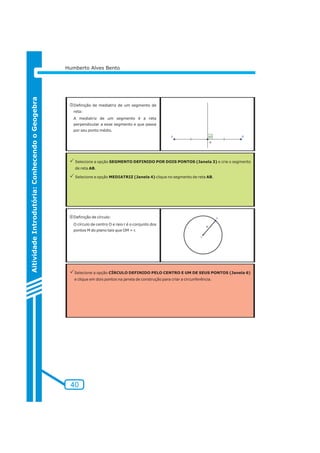
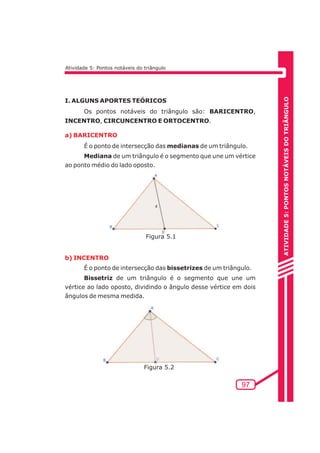
Obs: A propriedade a ser identificada ao mover os pontos A, B e C
é que a circunferência está sempre inscrita no triângulo, ou seja, a
circunferência está sempre dentro do triângulo.
e) Uma Propriedade para o Incentro
A reta que une o vértice A de um triângulo [ABC] com o
incentro I corta a circunferência circunscrita num ponto P
equidistante de B, de I e de C.
Analise a seguinte figura e tente você fazer no Geogebra.
Figura 5.2.2](https://image.slidesharecdn.com/possibilidadescomgeogebra-140902145022-phpapp02/85/Possibilidades-com-geogebra-108-320.jpg)
![Humberto Alves Bento
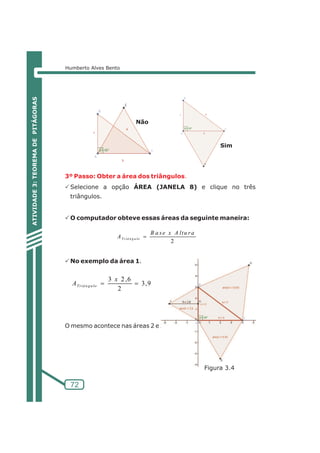
f) Circunferência Exinscritas Exincentros
106
O ponto I, incentro de um triângulo [ABC], é o único ponto
interior que é equidistante dos lados do triângulo. Mas há pontos
exteriores com a mesma propriedade do incentro. Chamamos-lhes
exincentros. Basta pensar nas intersecções das bissetrizes
exteriores dos ângulos do triângulo. Aliás, pelo ponto de encontro
das bissetrizes exteriores de A e C também passa a bissetriz
interior de B. (Pode provar que as bissetrizes exteriores de A e C
se intersectam e que a bissetriz exterior de A é perpendicular à
bissetriz interior de A, ou que as bissetrizes interiores de [ABC]
contêm as alturas de [LMN]). É claro que você pode e deve mover
os vértices do triângulo para ver que o resultado não depende de
qualquer triângulo em particular.
Agora com base na figura e no texto tente montar no
GeoGebra os exincentros.
ATIVIDADE 5: PONTOS NOTÁVEIS DO TRIÃNGULO
Figura 5.2.3](https://image.slidesharecdn.com/possibilidadescomgeogebra-140902145022-phpapp02/85/Possibilidades-com-geogebra-109-320.jpg)








![ATIVIDADE 5: PONTOS NOTÁVEIS DO TRIÃNGULO
115
Atividade 5: Pontos notáveis do triângulo
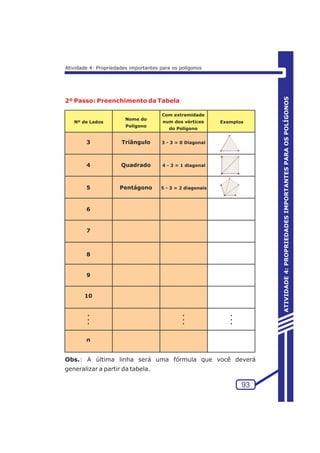
Pergunta 3: Quando que o ponto O (ortocentro) coincidirá
com um dos vértices do triângulo?
a) ( ) Quando o triângulo for “Agudo”. (Três ângulos internos
menores que 90º)
b) ( ) Quando o triângulo for “Retângulo”. (Um ângulo interno
igual a 90º)
c) ( ) Quando o triângulo for “Obtuso”. (Um ângulo interno
maior que 90º)
j) Propriedade interessante envolvendo o Ortocentro
Objetivo: Construir um triângulo ABC cujo ponto notável
seja o ortocentro para verificar a propriedade abaixo.
As paralelas aos lados de um triângulo ABC que passam
pelos vértices opostos, formam um triângulo A'B'C' em que A'B' =
2 AB, A'C' = 2 AC e B'C' = 2BC, em que A, B e C são os pontos
médios de B'C', A'C' e A'B' respectivamente.
Como conseqüência, as alturas do triângulo [ABC] são as
mediatrizes de [A'B'C']. As três alturas de um triângulo (que são
afinal mediatrizes de um outro triângulo) cortam-se num ponto H.
H é o ortocentro do triângulo [ABC] e o circuncentro de [A'B'C'].
1ª parte
Construa um triângulo ABC cujo ponto notável seja o
ortocentro (H).
2ª Parte (Construção da propriedade)
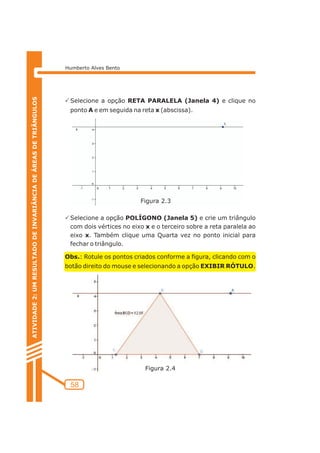
PSelecione a opção RETA PARALELA (Janela 4) e crie a reta
paralela a AB passando por C, a reta paralela a AC passando por
B, também a reta paralela a BC passando por A.](https://image.slidesharecdn.com/possibilidadescomgeogebra-140902145022-phpapp02/85/Possibilidades-com-geogebra-118-320.jpg)

![ATIVIDADE 5: PONTOS NOTÁVEIS DO TRIÃNGULO
117
Atividade 5: Pontos notáveis do triângulo
Obs.:
jNo triângulo ABC o ponto H é ortocentro (Encontro das alturas
do triângulo).
kNo triângulo A'B'C' o ponto H é circuncentro (Encontro das
mediatrizes do triângulo).
AB
AC
BC
2 x AB
2 x AC
2 x BC
A’B’
B’C’
A’C’
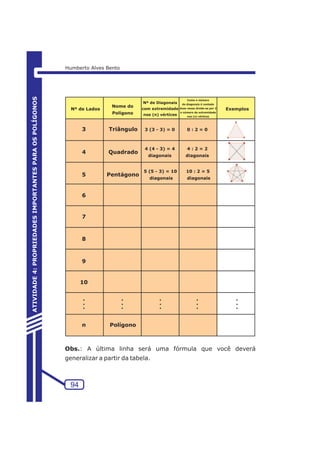
k) Um lugar Geométrico interessante para o Ortocentro
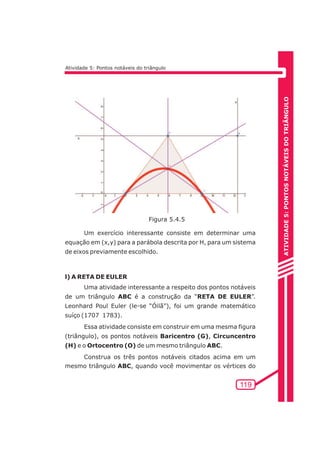
Quando um vértice C, no caso da figura, de um triângulo
[ABC] se desloca sobre uma paralela ao lado oposto (AB), o
ortocentro H descreve uma parábola.
PSelecione a opção PONTO (Janela 2). Clique em qualquer
ponto da janela de construção.
Figura 5.4.3](https://image.slidesharecdn.com/possibilidadescomgeogebra-140902145022-phpapp02/85/Possibilidades-com-geogebra-120-320.jpg)
































![PSelecione a opção ESCONDER/MOSTRAR (Janela 10).
Clique nas bissetrizes e nas circunferências para escondê-las.
PSelecione a opção ARCO CIRCUMCIRCULAR DADOS TRÊS
PONTOS (Janela 6).
Crie os arcos: AE, EG, GJ, JN, NL, LQ, QS e SU.
Obs.: Para criar o arco AE, você deverá clicar em A, P e E. Faça o
mesmo para os outros arcos.
PClique com o botão direito do mouse em cima do Arco
Circumcircular [A, P, E] e selecione a opção PROPRIEDADES
depois a opção ESTILO e aumente a espessura do arco. Faça
isso com todos os arcos.
Agora vamos criar uma ferramenta no Geogebra que, dado
um segmento qualquer, ela criará a Espiral Logarítmica.
ATIVIDADE 6: RAZÃO ÁUREA
153
Atividade 6: Razão Áurea
Figura 6.5.2](https://image.slidesharecdn.com/possibilidadescomgeogebra-140902145022-phpapp02/85/Possibilidades-com-geogebra-156-320.jpg)








