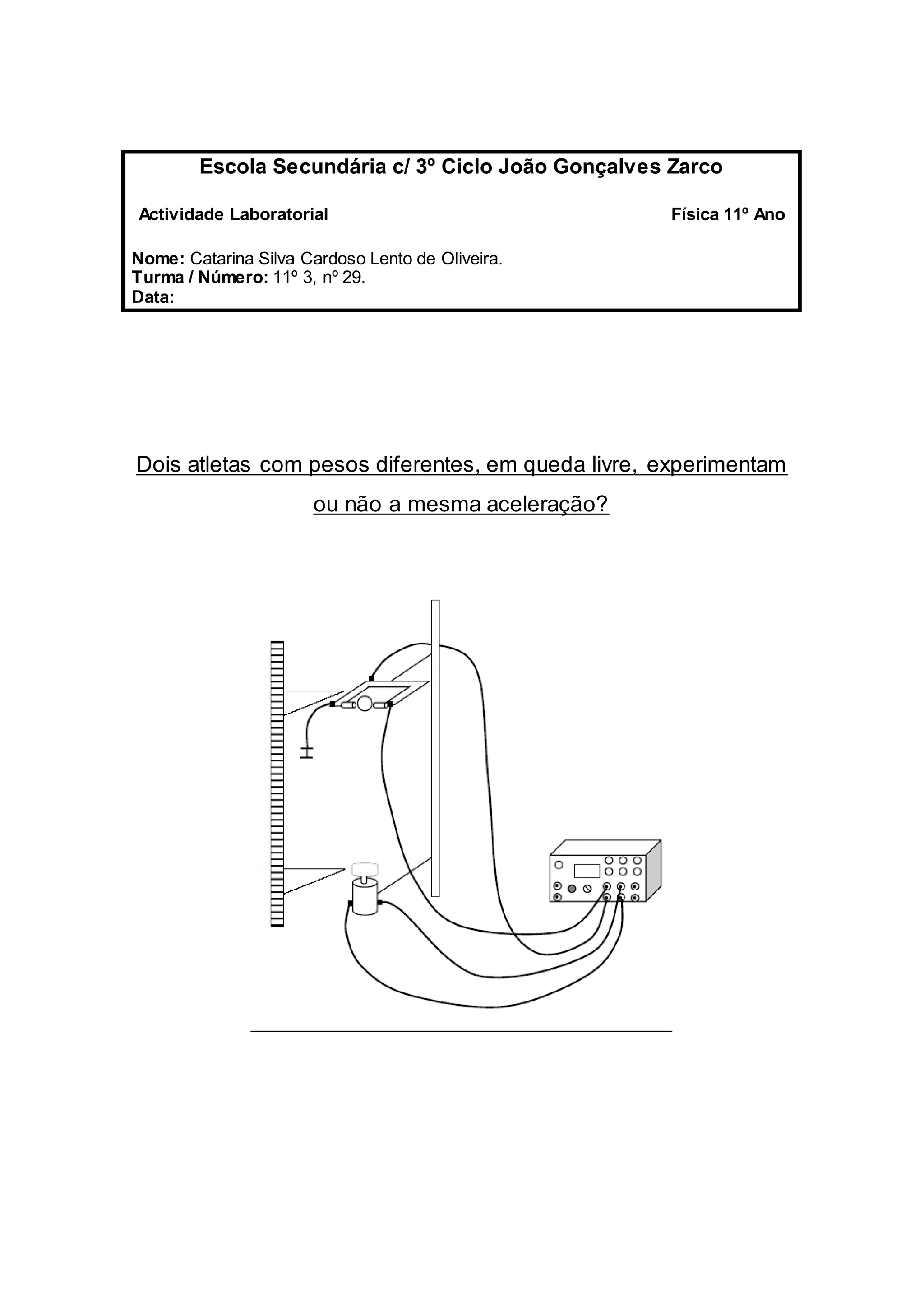
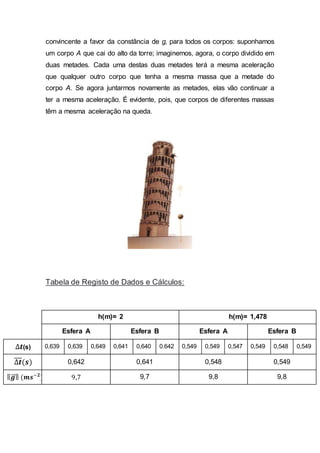
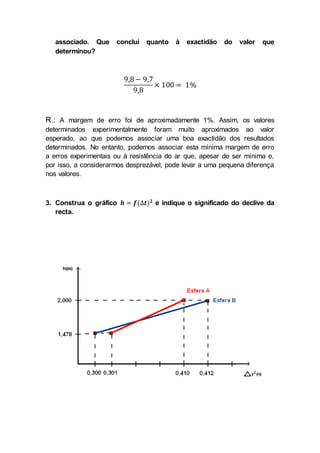
Este documento descreve um experimento para medir a aceleração da gravidade usando duas esferas de massas diferentes largadas de diferentes alturas. Os resultados mostraram que a aceleração da gravidade é independente da massa do corpo e da altura, com valores médios de aproximadamente 9,7-9,8 m/s2, próximos ao valor esperado de 9,8 m/s2.

1. Dois atletas com pesos diferentes, em queda livre, experimentam
ou não a mesma aceleração?
Escola Secundária c/ 3º Ciclo João Gonçalves Zarco
Actividade Laboratorial Física 11º Ano
Nome: Catarina Silva Cardoso Lento de Oliveira.
Turma / Número: 11º 3, nº 29.
Data:

2. Introdução:
Esta experiência consiste em libertar duas esferas de metal com diferentes
massas de uma determinada altura e medir o tempo que elas demoram a
atingir um ponto base predefinido e sempre fixo. Um dos objectivos é
encontrar o valor de g (aceleração da gravidade) para o local da experiência
e fazer uma analogia ao seu valor convencional de 9,8 𝑚𝑠−2
.
Objectivos:
 Distinguir força, velocidade e aceleração;
 Reconhecer que, numa queda livre, corpos com massas diferentes
experimentam a mesma aceleração;
 Explicar que os efeitos de resistência do ar ou de impulsão podem
originar acelerações de queda diferentes;
 Determinar, a partir das medições efectuadas, o valor da
aceleração da gravidade e compará-lo com o valor tabelado;
 Determinar, a partir das medições efectuadas o valor da velocidade
imediatamente antes de atingir o solo;
 Determinar o tempo de queda do corpo.
Material Necessário:
 Cronómetro digital de terminal “fone”;
 Adaptador de queda livre com esferas metálicas;
 Tripé com varão de suporte;
 Fita métrica.

3. Procedimento:
1. Fixa-se o mecanismo libertador do adaptador a um varão de suporte,
fixo num tripé, a uma altura (h) a cerca de 2m do solo;
2. Coloca-se uma das esferas no referido mecanismo, fixando-a
apertando levemente o parafuso;
3. Coloca-se o tapete receptor dentro de uma caixa baixa, no solo, na
vertical da esfera;
4. Mede-se, com a fita métrica, a distância do centro da esfera à base
do tapete receptor;
5. Conecta-se o terminal “fone” do adaptador ao cronómetro;
6. Liga-se o medidor em ON e coloca-se no modo GATE e ms;
7. Pressiona-se o botão RESET do medidor de tempo;
8. Desaperta-se o parafuso para libertar a esfera e verifica-se se cai no
centro do tapete receptor;
Se não cair, faz-se RESET no medidor de tempo, reposiciona-se o
tapete e verifica-se de novo;
9. Realiza-se o primeiro ensaio, deixando cair a esfera A;
10.Lê-se o tempo no mostrador digital do medidor e regista-se o valor na
tabela;
11.Repete-se o procedimento anterior mais duas vezes;
12.Substitui-se a esfera utilizada por outra diferente e repetem-se os
procedimentos de 8 a 11;
13.Registam-se os valores ∆𝑡 na tabela;
14.Repetem-se novamente os procedimentos anteriores tendo o
mecanismo libertador a uma altura (h) diferente, por exemplo, 1,5m, e
registam-se os novos valores de ∆𝑡 na tabela;
15.Completa-se a tabela realizando os cálculos necessários e indicando
as unidades.
Fundamentação Teórica:
A queda livre é o movimento de um corpo que, partindo do repouso e
desprezando a resistência do ar, está sujeito apenas à interacção gravítica.
Foi Galileu Galilei que demonstrou que corpos de massas diferentes quando
largados de uma determinada altura (h) chegam ao solo ao mesmo tempo,
desprezando a resistência do ar. Sabemos hoje que, nas proximidades do
planeta Terra, todos os corpos soltos num mesmo local são atraídos com
uma aceleração constante, quaisquer que sejam as suas massas.
Essa aceleração, de mesmo valor para todos os corpos, é denominada
aceleração normal da gravidade ( ) e o seu valor, a uma latitude de 45º e

4. ao nível das águas do mar é de aproximadamente 9,8 ms-2. A única força
que actua sobre o corpo é a força gravítica ( ).
Questões Pré-Laboratoriais:
1) a) Suponha que um corpo é deixado cair. Represente a(s) força(s)
que actuam sobre ele, assim como os vectores velocidade e
aceleração, se a resistência do ar for desprezável. O movimento é
acelerado ou retardado?
R.: A componente vertical da velocidade aumenta linearmente com o tempo,
pelo que o movimento é uniformemente variado (neste caso, acelerado), já que
o módulo da velocidade aumenta.
b) Responda às questões anteriores para o caso de um corpo ser
lançado para cima e estar na fase de subida.

5. R.: A componente vertical da velocidade aumenta linearmente com o tempo,
pelo que o movimento é uniformemente variado (neste caso, retardado), já que
o módulo da velocidade diminui.
c) A Terra estará em queda livre à volta do Sol? Se sim, por que não cai
para o Sol?
R.: Sim, a Terra está em queda livre à volta do Sol.
A Terra não cai para o Sol tal como uma pedra, porque o movimento tem de
obedecer à força, mas não tem de seguir a força.
A Terra tem movimentos circulares devido ao que chamamos condições
iniciais: quando se formou o Sistema Solar, há cerca de 4 500 milhões de
anos, a Terra começou a circular em volta do Sol e a sua velocidade era já
nessa altura como é hoje: mantém o seu valor, mas muda
permanentemente de direcção. A velocidade é sempre tangente à
trajectória. A força gravitacional, que aponta sempre para o centro da órbita,
mantém tal situação. Assim tem sido e assim continuará a ser. Se
imaginarmos que a força gravitacional cessava de repente, a Terra sairia
disparada da sua órbita e o Sol sairia da sua órbita em torno do centro da
Galáxia. Sem forças gravíticas, os astros ficariam todos com movimento
rectilíneo e uniforme.
Curiosidade:
Experiências pouco cuidadosas podem dar a impressão de que a
aceleração da gravidade varia de acordo com a massa dos corpos; por
exemplo, uma folha de papel amachucada e outra aberta podem cair em
tempos diferentes: isto ocorre devido à resistência do ar. Os antigos gregos
acreditavam firmemente que isto se devia às propriedades intrínsecas dos
corpos (quanto mais pesado o corpo, maior a sua velocidade de queda).
Galileu mostrou que este não era o caso, soltando vários corpos do alto da
Torre de Pisa, segundo a “lenda”. Além disso, usou um argumento muito

6. convincente a favor da constância de g, para todos os corpos: suponhamos
um corpo A que cai do alto da torre; imaginemos, agora, o corpo dividido em
duas metades. Cada uma destas duas metades terá a mesma aceleração
que qualquer outro corpo que tenha a mesma massa que a metade do
corpo A. Se agora juntarmos novamente as metades, elas vão continuar a
ter a mesma aceleração. É evidente, pois, que corpos de diferentes massas
têm a mesma aceleração na queda.
Tabela de Registo de Dados e Cálculos:
h(m)= 2 h(m)= 1,478
Esfera A Esfera B Esfera A Esfera B
∆𝒕(s) 0,639 0,639 0,649 0,641 0,640 0.642 0,549 0,549 0,547 0,549 0,548 0,549
∆𝒕̅̅̅(𝒔) 0,642 0,641 0,548 0,549
‖ 𝒈⃗⃗ ‖ (𝒎𝒔−𝟐
) 9,7 9,7 9,8 9,8

7. Cálculos da aceleração da Esfera A, com h=2m:
𝑥( 𝑡) = 𝑥0 + 𝑣0 𝑡 +
1
2
𝑎𝑡2
↔ 0 = 2 + (0 × 0,642) +
1
2
× 𝑎 × (0,642)2
↔
↔ 0 = 2 +
1
2
× 𝑎 × (0,642)2
↔ −2 =
1
2
× 𝑎 × (0,642)2
↔ 𝑎 = 9,7 𝑚𝑠−2
Cálculos da aceleração da Esfera B, com h=2m:
𝑥( 𝑡) = 𝑥0 + 𝑣0 𝑡 +
1
2
𝑎𝑡2
↔ 0 = 2 + (0 × 0,641) +
1
2
× 𝑎 × (0,641)2
↔
↔ 0 = 2 +
1
2
× 𝑎 × (0,641)2
↔ −2 =
1
2
× 𝑎 × (0,641)2
↔ 𝑎 = 9,7 𝑚𝑠−2
Cálculos da aceleração da Esfera A, com h=1,478m:
𝑥( 𝑡) = 𝑥0 + 𝑣0 𝑡 +
1
2
𝑎𝑡2
↔ 0 = 2 + (0 × 0,548) +
1
2
× 𝑎 × (0,548)2
↔
↔ 0 = 2 +
1
2
× 𝑎 × (0,548)2
↔ −2 =
1
2
× 𝑎 × (0,548)2
↔ 𝑎 = 9,8 𝑚𝑠−2
Cálculos da aceleração da Esfera B, com h=1,478m:
𝑥( 𝑡) = 𝑥0 + 𝑣0 𝑡 +
1
2
𝑎𝑡2
↔ 0 = 2 + (0 × 0,549) +
1
2
× 𝑎 × (0,549)2
↔
↔ 0 = 2 +
1
2
× 𝑎 × (0,549)2
↔ −2 =
1
2
× 𝑎 × (0,549)2
↔ 𝑎 = 9,8 𝑚𝑠−2

8. Dedução do valor de 𝑔:
𝑭𝒈 = 𝑮 ×
𝑴 𝑻×𝒎
𝒅 𝟐
, em que d é dado pela expressão: 𝒅 = 𝑹 𝑻+𝒉
Visto que h é muito menor que 𝑅 𝑇 , podemos usar a expressão aproximada:
𝑭𝒈 = 𝑮 ×
𝑴 𝑻×𝒎
𝑹 𝑻
𝟐 = 𝒎 × 𝒂, em que a=g
Simplificando:
𝒈 =
𝑮 × 𝑴 𝑻
𝑹 𝑻
𝟐
Questões Pós-Laboratoriais:
1. Compare os vários valores encontrados e tire conclusões.
R.: Através dos valores médios calculados experimentalmente pudemos
concluir que a aceleração da gravidade de um corpo é independente da
massa do mesmo e da altura a que este se encontra, desprezando a
resistência do ar.
2. Compare um valor médio calculado experimentalmente com o valor
conhecido da aceleração da gravidade e indique o erro percentual

9. associado. Que conclui quanto à exactidão do valor que
determinou?
9,8− 9,7
9,8
× 100 = 1%
R.: A margem de erro foi de aproximadamente 1%. Assim, os valores
determinados experimentalmente foram muito aproximados ao valor
esperado, ao que podemos associar uma boa exactidão dos resultados
determinados. No entanto, podemos associar esta mínima margem de erro
a erros experimentais ou à resistência do ar que, apesar de ser mínima e,
por isso, a considerarmos desprezável, pode levar a uma pequena diferença
nos valores.
3. Construa o gráfico 𝒉 = 𝒇(∆𝒕) 𝟐
e indique o significado do declive da
recta.

10. R.: O declive das rectas representadas no gráfico representa metade da
aceleração(
1
2
𝑎).
Conclusão:
Neste trabalho, concluímos que o valor da aceleração da gravidade (g) é
independente da massa do corpo em queda livre e para lugares próximos
da superfície da Terra (onde a resistência do ar é desprezada), assim
como da altura a que ele se encontra.
Os valores obtidos na experiência foram bastante satisfatórios, uma vez
que o resultado final foi bastante próximo do esperado.
Bibliografia:
 http://www.notapositiva.com/trab_estudantes/trab_estudantes/fisico
_quimica/quimica_11_ano.htm
 Ventura, Graça; Fiolhais, Manuel; Fiolhais, Carlos; Paiva, João;
Ferreira, António José; 11F – Física e Química A – Bloco2; Texto
Editores; 2008; Lisboa, Portugal.