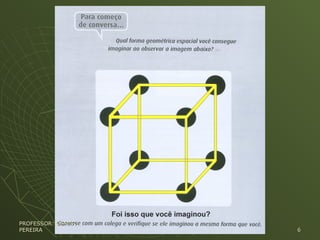
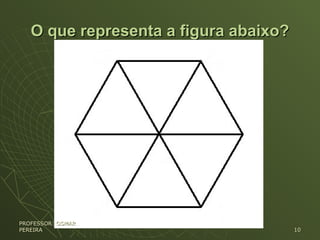
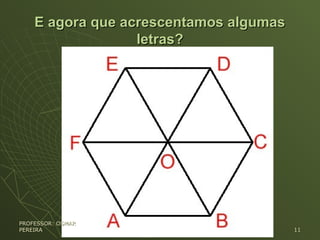
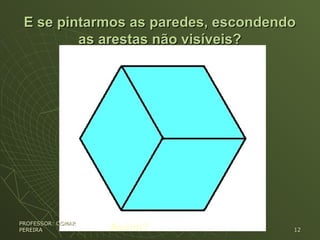
O documento discute a importância da leitura e da escrita na educação e apresenta exemplos de problemas que envolvem interpretação de texto e raciocínio lógico-matemático. O autor argumenta que uma boa compreensão do enunciado é essencial para resolver corretamente esses problemas, independentemente da disciplina envolvida.