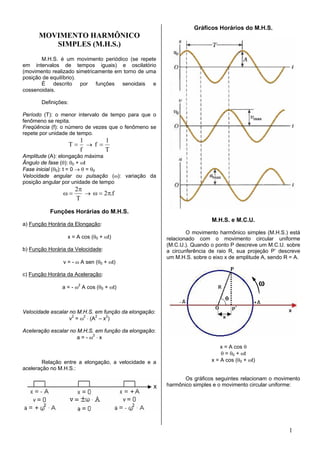
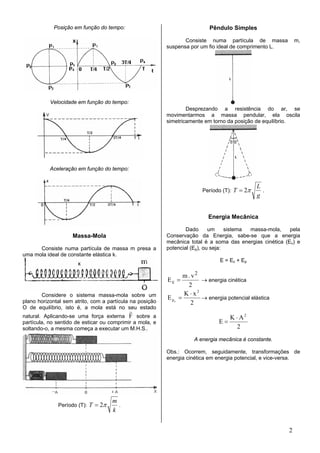
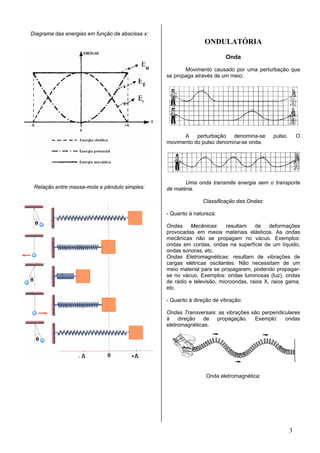
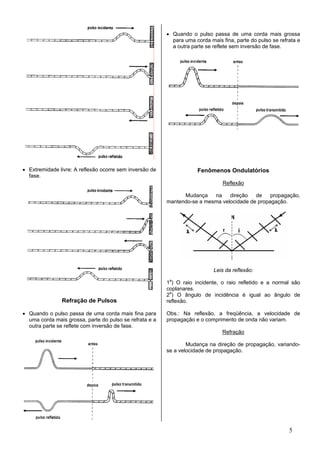
Este documento descreve os conceitos fundamentais do movimento harmônico simples e das ondas, incluindo suas definições, funções horárias, relações entre velocidade, aceleração e elongação, exemplos como o pêndulo e a massa-mola, além de fenômenos ondulatórios como reflexão, refração, interferência, difração e polarização.

1. Gráficos Horários do M.H.S.
MOVIMENTO HARMÔNICO
SIMPLES (M.H.S.)
M.H.S. é um movimento periódico (se repete
em intervalos de tempos iguais) e oscilatório
(movimento realizado simetricamente em torno de uma
posição de equilíbrio).
É descrito por funções senoidais e
cossenoidais.
Definições:
Período (T): o menor intervalo de tempo para que o
fenômeno se repita.
Freqüência (f): o número de vezes que o fenômeno se
repete por unidade de tempo.
1 1
T= → f =
f T
Amplitude (A): elongação máxima
Ângulo de fase (θ): θ0 + ωt
Fase inicial (θ0): t = 0 → θ = θ0
Velocidade angular ou pulsação (ω): variação da
posição angular por unidade de tempo
2π
ω= → ω = 2π.f
T
Funções Horárias do M.H.S.
M.H.S. e M.C.U.
a) Função Horária da Elongação:
O movimento harmônico simples (M.H.S.) está
x = A cos (θ0 + ωt) relacionado com o movimento circular uniforme
(M.C.U.). Quando o ponto P descreve um M.C.U. sobre
b) Função Horária da Velocidade: a circunferência de raio R, sua projeção P’ descreve
um M.H.S. sobre o eixo x de amplitude A, sendo R = A.
v = - ω A sen (θ0 + ωt)
c) Função Horária da Aceleração:
a = - ω2 A cos (θ0 + ωt)
Velocidade escalar no M.H.S. em função da elongação:
v2 = ω2 ⋅ (A2 – x2)
Aceleração escalar no M.H.S. em função da elongação:
a = - ω2 ⋅ x
x = A cos θ
θ = θ0 + ωt
Relação entre a elongação, a velocidade e a x = A cos (θ0 + ωt)
aceleração no M.H.S.:
Os gráficos seguintes relacionam o movimento
harmônico simples e o movimento circular uniforme:
1

2. Posição em função do tempo: Pêndulo Simples
Consiste numa partícula de massa m,
suspensa por um fio ideal de comprimento L.
Velocidade em função do tempo:
Desprezando a resistência do ar, se
movimentarmos a massa pendular, ela oscila
simetricamente em torno da posição de equilíbrio.
Aceleração em função do tempo:
L
Período (T): T = 2π .
g
Energia Mecânica
Dado um sistema massa-mola, pela
Massa-Mola Conservação da Energia, sabe-se que a energia
mecânica total é a soma das energias cinética (Ec) e
Consiste numa partícula de massa m presa a potencial (Ep), ou seja:
uma mola ideal de constante elástica k.
E = Ec + Ep
m . v2
Ec = → energia cinética
2
Considere o sistema massa-mola sobre um K ⋅ x2
E pe = → energia potencial elástica
plano horizontal sem atrito, com a partícula na posição 2
O de equilíbrio, isto é, a mola está no seu estado
r
natural. Aplicando-se uma força externa F sobre a K ⋅ A2
partícula, no sentido de esticar ou comprimir a mola, e E=
soltando-o, a mesma começa a executar um M.H.S.. 2
A energia mecânica é constante.
Obs.: Ocorrem, seguidamente, transformações de
energia cinética em energia potencial, e vice-versa.
m
Período (T): T = 2π .
k
2

3. Diagrama das energias em função da abscissa x:
ONDULATÓRIA
Onda
Movimento causado por uma perturbação que
se propaga através de um meio.
A perturbação denomina-se pulso. O
movimento do pulso denomina-se onda.
Uma onda transmite energia sem o transporte
Relação entre massa-mola e pêndulo simples: de matéria.
Classificação das Ondas:
- Quanto à natureza:
Ondas Mecânicas: resultam de deformações
provocadas em meios materiais elásticos. As ondas
mecânicas não se propagam no vácuo. Exemplos:
ondas em cordas, ondas na superfície de um líquido,
ondas sonoras, etc.
Ondas Eletromagnéticas: resultam de vibrações de
cargas elétricas oscilantes. Não necessitam de um
meio material para se propagarem, podendo propagar-
se no vácuo. Exemplos: ondas luminosas (luz), ondas
de rádio e televisão, microondas, raios X, raios gama,
etc.
- Quanto à direção de vibração:
Ondas Transversais: as vibrações são perpendiculares
à direção de propagação. Exemplo: ondas
eletromagnéticas.
Onda eletromagnética:
3

4. Como a propagação de um pulso é um
movimento uniforme, tem-se:
∆s
v=
∆t
λ
v= → v = λ⋅f
T
Ondas Longitudinais: as vibrações ocorrem na mesma Observação:
direção de propagação. Exemplo: ondas sonoras. A freqüência de uma onda é a freqüência da
fonte que a produziu, e não depende do meio de
propagação da onda, enquanto o comprimento de onda
λ e a velocidade propagação v variam com a mudança
do meio de propagação.
Exemplo: Uma onda de raio X muda de comprimento
Onda sonora: de onda e de velocidade quando entra no corpo
humano, mas não altera a sua freqüência.
Velocidade de propagação de uma onda em
uma corda tracionada
- Quanto à direção de propagação: Seja µ a densidade linear de massa da corda:
m
Ondas Unidimensionais: se propagam em uma direção
µ = , onde m é a massa da corda e L é o
L
(comprimento), como as ondas em corda, que é um comprimento da corda.
meio unidimensional. A velocidade de propagação v é dada por:
Ondas Bidimensionais: se propagam em duas direções
(superfície), como as ondas na superfície de um
líquido, que é um meio bidimensional. F
Ondas Tridimensionais: se propagam em três direções
v= ,
µ
(espaço), como as ondas sonoras e as ondas
luminosas.
onde F é a força de tração exercida na corda.
Ondas Periódicas
Conclusões:
Sucessão de pulsos iguais, que se propagam • A onde se propaga com maior velocidade na
em espaços e tempos iguais (se repetem corda de menor densidade linear.
periodicamente). • A onda se propaga com maior velocidade na
corda mais tracionada.
Reflexão de Pulsos
• Extremidade fixa: A reflexão ocorre com inversão de
fase.
A parte mais alta denomina-se crista e a parte
mais baixa denomina-se vale.
Definições:
Comprimento de onda (λ): distância entre duas cristas
consecutivas ou dois vales consecutivos.
Amplitude (A): valor máximo da elongação.
Período (T): intervalo de tempo de uma oscilação
completa.
Freqüência (f): número de oscilações por unidade de
tempo.
4

5. • Quando o pulso passa de uma corda mais grossa
para uma corda mais fina, parte do pulso se refrata e
a outra parte se reflete sem inversão de fase.
• Extremidade livre: A reflexão ocorre sem inversão de Fenômenos Ondulatórios
fase.
Reflexão
Mudança na direção de propagação,
mantendo-se a mesma velocidade de propagação.
Leis da reflexão:
1a) O raio incidente, o raio refletido e a normal são
coplanares.
2a) O ângulo de incidência é igual ao ângulo de
Refração de Pulsos reflexão.
• Quando o pulso passa de uma corda mais fina para Obs.: Na reflexão, a freqüência, a velocidade de
uma corda mais grossa, parte do pulso se refrata e a propagação e o comprimento de onda não variam.
outra parte se reflete com inversão de fase.
Refração
Mudança na direção de propagação, variando-
se a velocidade de propagação.
5

6. Se as duas ondas de fases opostas tivessem a
mesma amplitude em módulo, uma iria destruir a outra
Leis da refração:
e a onda resultante seria nula no momento do
cruzamento.
1a) O raio incidente, o raio refratado e a normal são
Após a superposição, cada onda se propaga
coplanares.
independentemente da outra, com as mesmas
2a) Lei de Snell – Descartes:
características que tinham anteriormente.
sen i n 2 λ1 v1
= = =
sen r n 1 λ 2 v 2 Observação:
No caso de interferência de ondas luminosas,
n1 e n2 → índices de refração absoluta dos meios 1 e 2. os pontos onde a interferência é construtiva aparecem
Aplicando a Lei de Snell, temos: brilhantes e os pontos onde a interferência é destrutiva
• n2 > n1 ⇒ λ2 < λ1 ⇒ v2 < v1 ⇒ r < i aparecem escuros. No caso de ondas sonoras, a
• n2 < n1 ⇒ λ2 > λ1 ⇒ v2 > v1 ⇒ r > i interferência construtiva ou destrutiva é evidenciada por
um aumento ou uma diminuição, respectivamente, da
Obs.: Na refração, a freqüência não varia, mas a intensidade do som ouvido.
velocidade de propagação e o comprimento de onda
variam. Ondas Estacionárias
Ondas resultantes da superposição de duas
Superposição ou Interferência de Ondas ondas de mesma freqüência, mesma amplitude,
mesmo comprimento de onda, mesma direção e
Encontro ou cruzamento de duas ou mais sentidos opostos.
ondas que se propagam, simultaneamente, num Pode-se obter uma onda estacionária através
mesmo meio. de uma corda fixa numa das extremidades.
No ponto em que ocorre a superposição de
duas ou mais ondas, o efeito resultante é a soma dos
efeitos individuais de cada onda.
• Quando as ondas produzem deslocamentos no
mesmo sentido, a amplitude da onda resultante é
aumentada, produzindo uma interferência construtiva.
N = nós; V= ventres
Com uma fonte faz-se a outra extremidade
vibrar com movimentos verticais periódicos,
produzindo-se pulsos regulares que se propagam pela
corda.
• Quando as ondas produzem deslocamentos em Ao atingirem a extremidade fixa, as ondas se
sentidos opostos, a amplitude da onda resultante é refletem, retornando com sentido de deslocamento
diminuída, produzindo uma interferência destrutiva. contrário ao anterior.
Dessa forma, as ondas refletidas se superpõem
às ondas incidentes, originando ondas estacionárias.
Uma onda estacionária se caracteriza pela
amplitude variável de ponto para ponto, isto é, há
pontos da corda que não se movimentam, pois
6

7. apresentam amplitude nula (interferência destrutiva), propagação. Polarizar uma onda é fazê-la vibrar em
chamados nós, e pontos que vibram com amplitude apenas uma direção, tornando-se uma onda
máxima (interferência construtiva), chamados ventres. polarizada.
Entre os nós, os pontos da corda vibram com a Suponha que a mão da pessoa indicada na
mesma freqüência, mas com amplitudes diferentes. figura realize um movimento circular uniforme em torno
do eixo da corda, fixa numa parede por uma de suas
Observações: extremidades e a outra, na mão da pessoa.
λ
- A distância entre dois nós consecutivos vale .
2
λ
- A distância entre dois ventres consecutivos vale .
2
Obtemos, neste caso, uma onda que vibra em
- A distância entre um nó e um ventre consecutivos
planos diferentes, denominada onda não polarizada. A
λ corda vibra em todas as direções perpendiculares à
vale .
4 direção de propagação da onda.
- A onda estacionária não transmite energia de ponto Quando a pessoa realiza um movimento
para ponto da corda, pois as energias cinética e vibratório numa única direção que é perpendicular ao
potencial ficam localizadas entre os nós. eixo da corda, isto é, a mão da pessoa se move
verticalmente para cima e para baixo, as partículas da
corda vibram numa direção perpendicular à direção de
propagação da onda. Este tipo de onda é denominado
onda polarizada.
A polarização das ondas é efetuada por
dispositivos chamados polarizadores.
Difração
Fenômeno pelo qual uma onda tem a
capacidade de contornar um obstáculo, ao ser
parcialmente interrompida por ele, desde que o
obstáculo tenha dimensão comparável ao comprimento
de onda da onda incidente.
Obs.: A polarização é um fenômeno que ocorre
exclusivamente com as ondas transversais.
Quando os pontos da fenda são atingidos pela
frente de onda, eles se tornam fontes de ondas
secundárias, mudando a direção da onda incidente,
fazendo com que transponham o obstáculo.
Polarização
Uma onda não polarizada é aquela que possui
várias direções de vibração, em relação à direção da
7

8. A velocidade das ondas sonoras depende das
características do meio onde se propagam. Sua
velocidade é tanto maior quanto mais rígido o meio de
propagação: v sólidos > v líquidos > v gases
Qualidades fisiológicas do som
Altura: qualidade que permite classificar os sons em
graves e agudos, estando relacionada com a
freqüência do som.
graves → freqüência menor
agudos → freqüência maior
A voz do homem tem freqüência que varia
entre 100 Hz e 200 Hz e a da mulher entre 200 Hz e
400 Hz; portanto, a voz do homem é mais grave e a
voz da mulher é mais aguda.
Intensidade: qualidade que permite classificar os sons
em fortes e fracos, estando relacionada com a energia
transportada pela onda.
fracos → menor amplitude de vibração
fortes → maior amplitude de vibração
A intensidade mínima audível é chamada limiar
da percepção auditiva, e a máxima, limiar da sensação
dolorosa.
Timbre: qualidade que permite ao ouvido distinguir dois
sons de mesma altura e mesma intensidade, emitidos
por fontes diferentes, estando relacionado com a forma
das vibrações, isto é, com a forma da onda sonora.
ACÚSTICA Fenômenos Sonoros
O som é uma onda mecânica longitudinal, que Dos fenômenos ondulatórios (reflexão,
se propaga através de vibrações e ondas de refração, interferência, difração e polarização), uma
compressão e rarefação nos meios materiais; portanto, onda sonora só não sofre polarização, pois é uma onda
não se propaga no vácuo. longitudinal.
O ouvido, ao ser atingido por uma onda sonora
(o tímpano passa a vibrar com a mesma freqüência), Reflexão
converte a variação de pressão no ar em estímulo
nervoso, o qual, ao alcançar o cérebro, produz a Reforço: ocorre quando a diferença entre os instantes
sensação auditiva. de recebimento do som refletido e do som direto é
Elementos do canal auditivo: praticamente nula. O observador ouve o som direto
juntamente com o som refletido. Há somente um
aumento da intensidade sonora.
Reverberação: ocorre quando o som refletido atinge o
observador no momento em que o som direto está se
extinguindo, ocasionando o prolongamento da
sensação auditiva.
Eco: ocorre quando uma pessoa emite um som e
recebe, além do som direto, o som refletido em um
anteparo, após um intervalo de tempo maior que 0,1s.
Admitindo a velocidade do som no ar 340m/s, em 0,1s
o som percorre 34m, sendo 17m para atingir o anteparo
e 17m para voltar. Portanto, a menor distância de um
observador a um anteparo para provocar o eco deverá
ser 17m.
Velocidade do som:
8

9. Refração portanto, diferentes modos de vibração ou diferentes
harmônicos.
A onda sonora passa de um meio para outro,
mudando sua velocidade de propagação e o n = 1 → 1º harmônico ou som fundamental
comprimento de onda, mas mantendo constante a
freqüência.
Interferência
Consiste no recebimento de dois ou mais sons
de fontes diferentes. n = 2 → 2º harmônico
som forte → interferência construtiva
som fraco → interferência destrutiva
Obs.: Um caso particular de interferência sonora ocorre
quando há superposição de ondas sonoras de mesma
amplitude e freqüências ligeiramente diferentes.
n = 3 → 3º harmônico
Ouvem-se então os denominados batimentos, que
consistem em flutuações periódicas da intensidade do
som resultante ouvido.
Difração
O som contorna obstáculos, ou seja, as ondas
sonoras sofrem desvios nas extremidades dos
obstáculos que encontram. Desse modo, uma pessoa, n = 4 → 4º harmônico
atrás de uma parede, pode ouvir o som emitido por
uma fonte atrás dela.
Ressonância n = 5 → 5º harmônico
Fenômeno em que um sistema oscilante
começa a vibrar por influência de outro, que está
vibrando na mesma freqüência natural do sistema.
Se um sistema físico recebe energia
periodicamente, com uma freqüência igual à sua
freqüência natural de vibração, o sistema passa a O comprimento L da corda e o comprimento de
vibrar com amplitude crescente, que tende ao maior onda λ são tais que:
valor possível. λ 2L
No caso do som, a ressonância consiste numa L=n⋅ ou λ =
sobreposição de sons, provocando a sensação de que 2 n
o som foi reforçado.
Considerando a velocidade com que as ondas
Cordas Vibrantes propagam-se na corda, teremos:
v
Consideremos uma corda esticada e com suas v = λ. ⋅ f ⇒ f=
λ
duas extremidades fixas. Provocando uma perturbação
v v
na corda, estabelecem-se nela ondas transversais que, f= ⇒ fn = n ⋅ (n = 1, 2, 3 ...)
superpondo-se às ondas refletidas nas extremidades, 2L 2L
originam ondas estacionárias na corda.
n
Quando a corda vibra, faz com que o ar ao seu
redor vibre também, com a mesma freqüência; assim, a
As vibrações da corda transmitem-se para o ar freqüência f é a de vibração dos pontos da corda e
da região ao seu redor, dando origem às ondas também é a freqüência da onda sonora.
sonoras que terão a mesma freqüência de oscilação
dos pontos da corda. Freqüência de cada harmônico:
As extremidades fixas da corda serão os nós.
Entre elas haverá a formação de n ventres. Haverá,
9

10. v
• som fundamental: f1 =
2L
• n-ésimo harmônico: f n = n ⋅ f1
Obs.: A freqüência de qualquer harmônico é sempre i = 5 → 5º harmônico
um múltiplo inteiro do som fundamental.
Tubos Sonoros
Um tubo sonoro é uma coluna de ar na qual se
4L v
estabelecem ondas estacionárias longitudinais (através λ= → fi = i ⋅
da vibração do ar no interior do tubo), determinadas i 4L
pela superposição de ondas geradas numa f i = i ⋅ f 1 ; (i = 1, 3, 5 ...)
extremidade com as ondas refletidas na outra
extremidade. As ondas estacionárias fazem vibrar o ar
que envolve o tubo, dando origem a uma onda sonora. Obs.: No tubo fechado, obtêm-se freqüências naturais
Existem dois tipos de tubos sonoros: abertos e apenas dos harmônicos ímpares.
fechados. Nas extremidades abertas, formam-se
ventres (interferência construtiva); nas extremidades
fechadas, formam-se nós (interferência destrutiva). Efeito Doppler
Considere os tubos sonoros de comprimento L O efeito Doppler ocorre quando há uma
e a velocidade de propagação das ondas v: aproximação ou um afastamento entre o observador e
a fonte sonora, fazendo com que a freqüência da onda
Tubo aberto: possui as duas extremidades abertas. sonora percebida pelo observador seja diferente da
freqüência real da onda emitida pela fonte, devido ao
A distância entre dois ventres consecutivos é movimento relativo entre eles.
λ
igual a meio comprimento de onda: . 1º caso: observador em repouso e fonte em
2 movimento:
Quando a fonte sonora se aproxima de um
n = 1 → 1º harmônico ou som fundamental observador parado, este recebe mais ondas do que
receberia se a fonte estivesse parada (encurtamento
aparente do comprimento de onda). Nesta situação, a
freqüência percebida pelo observador (fO) é maior que
a freqüência do som emitido pela fonte (fF).
n = 2 → 2º harmônico Quando a fonte sonora se afasta de um
observador parado, este recebe menos ondas do que
receberia se a fonte estivesse parada (alongamento
aparente do comprimento de onda). Nesta situação, a
freqüência percebida pelo observador (fO) é menor que
n = 3 → 3º harmônico a freqüência do som emitido pela fonte (fF).
2º caso: fonte em repouso e observador em
movimento:
Ao se aproximar da fonte sonora, o observador
encontra uma maior quantidade de ondas do que
2⋅L v
λ = → fn = n ⋅ encontraria se estivesse parado; assim ele percebe
n 2L uma freqüência (f0) maior que a freqüência do som
emitido pela fonte (fF).
f n = n ⋅ f1 (n = 1, 2, 3 ...); n é o número de nós Ao se afastar da fonte sonora, o observador
encontra uma menor quantidade de ondas do que
Tubo fechado: possui uma extremidade fechada e outra encontraria se estivesse parado; assim ele percebe
aberta. uma freqüência (f0) menor que a freqüência do som
A distância entre um ventre e o nó consecutivo emitido pela fonte (fF).
λ
equivale a um quarto do comprimento de onda: . 3º caso: observador e fonte em movimento relativo
4
sobre a mesma reta.
i = 1 → 1º harmônico ou som fundamental
De acordo com a altura do som, maior
freqüência significa som mais agudo e menor
freqüência significa som mais grave.
i = 3 → 3º harmônico
10

11. Aproximação ⇒ f0 > fF ⇒ o som que o observador
recebe é mais agudo que o som da fonte.
Afastamento ⇒ f0 < fF ⇒ o som que o observador
recebe é mais grave que o som da fonte.
Para qualquer caso, vale a seguinte relação:
⎛ v ± vo ⎞
fo = fF ⋅ ⎜ S
⎜v ±v ⎟ ⎟
⎝ S F⎠
f0 : freqüência percebida pelo observador (freqüência
aparente)
fF : freqüência emitida pela fonte (freqüência real)
vS : velocidade do som
v0 : velocidade do observador
vF : velocidade da fonte
Convenção de Sinais:
Orienta-se um eixo positivamente do
observador (O) para a fonte (F).
• vO e vF estão no sentido positivo: adota-se o sinal +
• vO e vF estão no sentido negativo: adota-se o sinal –
⎧→ + observador se aproxima da fonte
vo ⎨
⎩← − observador se afasta da fonte
⎧→ + fonte se afasta do observador
vF ⎨
⎩← − fonte se aproxima do observador
vO = 0 → observador parado
vF = 0 → fonte parada
11