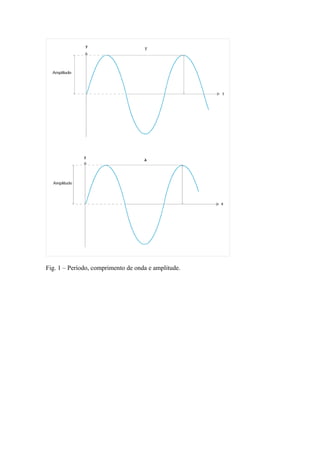
O documento discute as características fundamentais das ondas, incluindo: 1) Uma onda pode ser representada matematicamente por uma função que depende da posição no espaço e do tempo; 2) Características-chave de uma onda incluem período, frequência, comprimento de onda e amplitude; 3) Ondas podem se propagar transversalmente ou longitudinalmente em relação à direção do movimento.

1. Função de onda
As ondas periódicas possuem uma série de características que são geralmente comuns.
Vamos tentar representar uma onda matematicamente.
Sabemos que uma onda vai-se deslocando no tempo. Assim, se fixarmos um
determinado instante de tempo, a amplitude (ou noutro termos, o valor em altura que a
onda toma) vai variando desde uma posição mínima até uma máxima. Ou seja, por
exemplo, para t = 0 temos y(x,0) = f(x).
Esta função é ligeiramente diferente das que estamos habituados a ver. É mais comum
vermos uma função f(x) que contém apenas uma única variável e logo o valor da
imagem vai depender apenas desta variável. Contudo, pode acontecer que tenhamos
duas variáveis distintas que sejam necessárias de modo a sabermos qual o valor da
função. É o que vai acontecer para as ondas. Estas dependem de uma posição no espaço
x e de um valor no tempo t.
Se a onda se desloca no tempo ela irá fazê-lo com uma determinada velocidade v.
Imaginemos que ela se desloca para a direita. Neste caso após vt metros o valor da
amplitude vai ser o mesmo que em t = 0. Assim
y(x,t) = y(x − vt,0)
ou podemos representar da seguinte forma
y(x,t) = f(x − vt)
Caso a onda se deslocasse no sentido contrário teríamos
y(x,t) = f(x + vt)
A esta função y que depende de x e de t chamamos função de onda e é ela que nos
permite observar o comportamento geral da onda.
Podemos recordar da matemática que tipo de funções têm este comportamento
periódico. A função sin x tem exactamente a mesma forma que uma onda periódica e,
por isso, se chamam habitualmente ondas sinusoidais.

2. Período, frequência e comprimento de onda
Período
Característica essencial que caracteriza uma onda. Geralmente define-se pelo tempo que
um ciclo demora a ser percorrido e a sua unidade SI é o segundo (s).
Outras características estão associadas ao período.
Frequência
É dada pela expressão
Esta grandeza corresponde ao número de vezes que um ciclo é percorrido por unidade
de tempo e em unidades SI vem em s-1 ou Hz (em homenagem ao Físico Heirich Hertz).
Também associado à frequência e ao período há uma grandeza relacionada com a
distância.
Comprimento de Onda
É a distância que um ciclo tem no espaço.
Amplitude
Distância entre o ponto de equilíbrio da onda e o ponto de desvio máximo relativamente
a ele.
De um modo geral, as características de uma onda podem ser observadas no seguinte
esquema:

3. Fig. 1 – Período, comprimento de onda e amplitude.

4. Função de onda
De acordo com a figura 1, num instante t = 0, podemos definir que para x = 0 temos
y = 0. O mesmo se passa para x = λ/2 e para x = λ.
Tratando-se de uma onda sinusoidal, para isso acontecer temos sin λ =0 e para sin 0 =
0. Assim sendo, a função de onda pode ser escrita como:
Vamos verificar que é assim mesmo. Quando x = 0 temos sin 0 e quando x = λ/2 temos
sin π.
O que fizemos até agora foi para um instante de tempo fixo. Ora nós sabemos que uma
onda varia conforme o tempo. Vimos que para uma onda que se desloque para a direita
temos y(x,t) = f(x − v,t) pelo que
Velocidade de onda
É a velocidade de propagação da onda e define-se como
É a velocidade à qual um ponto, caracterizado por uma determinada fase, se desloca no
espaço.
Outras quantidades relacionadas com a velocidade ou a frequência são as que se
apresentam em seguida.
O número de onda (k) é o número de ondas que cabe num metro:
e a sua unidade SI é m-1.
A frequência angular vai ser
Com estas definições podemos já escrever a função de onda na forma mais habitual:

5. Representação gráfica da função de onda.
Representação gráfica da função de onda.
A fórmula mais habitual da frequência angular é
ω = kv
cuja unidade em SI é s-1.
Pode acontecer que para x = 0 e t = 0, y não seja 0. Quando isto acontece temos de
adicionar uma fase inicial φ, pelo que a função de onda é assim escrita de um modo
geral como: y(x,t) = A sin (kx - ωt + φ).
Chama-se ao argumento do seno, a fase. Podemos concluir que, quando a fase inicial
, então a função de onda pode ser escrita apenas com um coseno (através das
propriedades trigonométricas destas funções).
Este conceito de fase é importante em diversos campos da Física. É possível concluir
que diversas ondas com a mesma frequência e com o mesmo comprimento de onda
podem ter fases diferentes. Isto pode tornar-se importante quando queremos utilizar
diversas ondas juntas.

6. Propagação das ondas
Ondas transversais e longitudinais
É possível distinguir as ondas relativamente ao modo como se propagam. Existem dois
casos que se definem.
Onda transversal
Uma onda sinusoidal que se move perpendicularmente à direcção de propagação.
O caso do impulso na corda é um exemplo simples de uma onda deste tipo. Podemos
ver este caso tomando em atenção a direcção de propagação da onda.
Fig. 2 - Onda na corda.
Onda Longitudinal
Uma onda longitudinal move-se paralelamente à direcção de propagação.
Suponhamos que temos uma mola. O comportamento de uma mola a abanar também se
trata de uma onda. Neste caso, a zona comprimida vai-se deslocando ocupando os
lugares onde anteriormente estava uma zona expandida. Como este movimento é
repetido constantemente trata-se então de uma onda. Ora contrariamente ao caso da
corda, este fenómeno acontece na mesma direcção da propagação da onda.

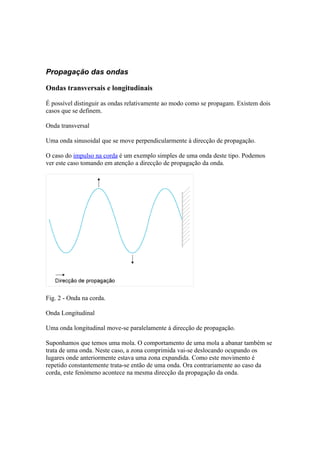
7. Fig. 3 - Mola com zonas comprimidas e distendidas.
As ondas sonoras são também um exemplo de ondas longitudinais.
LUZ
A luz é uma onda eletromagnética, cujo comprimento de onda se inclui num
determinado intervalo dentro do qual o olho humano é a ela sensível.[1] Trata-se, de
outro modo, de uma radiação electromagnética que se situa entre a radiação
infravermelha e a radiação ultravioleta. As três grandezas físicas básicas da luz são
herdadas das grandezas de toda e qualquer onda eletromagnética: intensidade (ou
amplitude), frequência e polarização (ângulo de vibração). No caso específico da luz, a
intensidade se identifica com o brilho e a frequência com a cor. Deve ser ressaltada
também a dualidade onda-partícula, característica da luz como fenômeno físico, em que
esta tem propriedades de onda e partículas, sendo válidas ambas as teorias sobre a
natureza da luz.
Um raio de luz é a trajetória da luz em determinado espaço, e sua representação indica
de onde a luz é criada (fonte) e para onde ela se dirige. O conceito de raio de luz foi
introduzido por Alhazen. Propagando-se em meio homogéneo, a luz percorre trajetórias
retilíneas; somente em meios não-homogêneos a luz pode descrever trajetórias curvas.