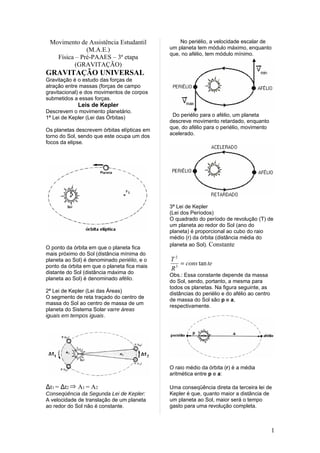
O documento resume as três leis de Kepler que descrevem o movimento planetário e a lei da gravitação universal de Newton. As leis de Kepler explicam que as órbitas planetárias são elípticas, que a área varrida em tempos iguais é a mesma, e que o quadrado do período é proporcional ao cubo do raio médio da órbita. A lei da gravitação de Newton estabelece que a força de atração entre dois corpos é diretamente proporcional ao produto de suas massas e inversamente propor

1. Movimento de Assistência Estudantil No periélio, a velocidade escalar de
(M.A.E.) um planeta tem módulo máximo, enquanto
que, no afélio, tem módulo mínimo.
Física – Pré-PAAES – 3ª etapa
(GRAVITAÇÃO)
GRAVITAÇÃO UNIVERSAL
Gravitação é o estudo das forças de
atração entre massas (forças de campo
gravitacional) e dos movimentos de corpos
submetidos a essas forças.
Leis de Kepler
Descrevem o movimento planetário.
1ª Lei de Kepler (Lei das Órbitas) Do periélio para o afélio, um planeta
descreve movimento retardado, enquanto
Os planetas descrevem órbitas elípticas em que, do afélio para o periélio, movimento
torno do Sol, sendo que este ocupa um dos acelerado.
focos da elipse.
3ª Lei de Kepler
(Lei dos Períodos)
O quadrado do período de revolução (T) de
um planeta ao redor do Sol (ano do
planeta) é proporcional ao cubo do raio
médio (r) da órbita (distância média do
planeta ao Sol). Constante
O ponto da órbita em que o planeta fica
mais próximo do Sol (distância mínima do
planeta ao Sol) é denominado periélio, e o T2
ponto da órbita em que o planeta fica mais = cons tan te
R3
distante do Sol (distância máxima do Obs.: Essa constante depende da massa
planeta ao Sol) é denominado afélio. do Sol, sendo, portanto, a mesma para
todos os planetas. Na figura seguinte, as
2ª Lei de Kepler (Lei das Áreas) distâncias do periélio e do afélio ao centro
O segmento de reta traçado do centro de de massa do Sol são p e a,
massa do Sol ao centro de massa de um respectivamente.
planeta do Sistema Solar varre áreas
iguais em tempos iguais.
O raio médio da órbita (r) é a média
aritmética entre p e a:
Δt1 = Δt2 ⇒ A1 = A2 Uma conseqüência direta da terceira lei de
Conseqüência da Segunda Lei de Kepler: Kepler é que, quanto maior a distância de
A velocidade de translação de um planeta um planeta ao Sol, maior será o tempo
ao redor do Sol não é constante. gasto para uma revolução completa.
1

2. Importante: As três leis de Kepler são atraído pela Terra com uma força
válidas para

gravitacional Fg . Esta força é a força peso
quaisquer sistemas em que corpos
gravitam em torno de um corpo central. do corpo de massa m.
Exemplos: planetas em torno do
Sol, Lua em torno da Terra, satélites
artificiais em torno da Terra.
Lei de Newton da Gravitação
Universal
Dois corpos, de massas m1 e m2, atraem-se
mutuamente com forças que têm a direção
da reta que os une e cujas intensidades
são diretamente proporcionais ao produto
das massas e inversamente proporcionais
ao quadrado da distância d que os separa.
m1 .m2
Fg = G
d2
P = Fg
G é a constante de gravitação universal: M .m
G = 6,67 ⋅ 10-11 N.m2/kg2 m.g = G
r2
O campo gravitacional é dado por:
M .m
g =G
( R + h) 2
Nos pontos da superfície da Terra:
M .m
g =G
R2
As forças gravitacionais mantêm os Esta expressão mostra que a intensidade
planetas em órbita em torno do Sol, bem do campo gravitacional decresce com o
como quaisquer corpos gravitam em torno quadrado da distância do corpo ao centro
de um corpo central. da Terra. Obs.: As expressões anteriores
são válidas para qualquer planeta, sendo M
Obs.: As forças gravitacionais obedecem à a massa do planeta e R o seu raio.
terceira lei de Newton (lei da ação e
reação). Satélites em Órbitas Circulares
Campo Gravitacional (aceleração da Considere um satélite de massa m
gravidade) descrevendo uma órbita circular de raio r
Quando dois corpos de massas M e m se em torno de um planeta de massa M.
atraem, dizemos que cada um deles se
encontra num campo de força gerado pelo
outro corpo, denominado campo
gravitacional g. Na região que envolve a
Terra, bem como qualquer outro planeta,
dizemos que há um campo gravitacional,
pois qualquer corpo colocado em suas
proximidades fica submetido à força de
atração gravitacional.
Considere um corpo de massa m situado
em um ponto a uma altura h em relação à
superfície da Terra, e sejam M e R a massa
e o raio da Terra, respectivamente. O vetor
campo gravitacional gerado pela Terra, que

atua no corpo, é representado por g , e
corresponde à aceleração da gravidade, à
Cálculo da velocidade de translação do
qual o corpo fica sujeito. O corpo será
satélite:
2

3. A força gravitacional que o planeta exerce Obs.: A velocidade de translação e o
no satélite é a resultante centrípeta que período de translação não dependem da
mantém o satélite em órbita. massa m do corpo em órbita, mas apenas
da massa M do corpo central. Importante: A
Fcp = Fg força de atração gravitacional que o planeta
exerce no satélite está sendo usada como
v2 Mm resultante centrípeta, que tem como função
m =G 2 manter os corpos em órbita. Por isso, os
r r corpos no interior do satélite flutuam
GM (imponderabilidade).
v=
r
sendo r = R + h, em que R é o raio do
planeta e h é a altura do satélite em relação
à superfície do planeta.
Obs.: Esta expressão da velocidade orbital
pode ser aplicada no movimento de
planetas em torno do Sol, considerando-se
a órbita elíptica como aproximadamente
circular.
Dedução da constante da 3ª lei de Kepler:
Da velocidade linear de um corpo em
M.C.U.,
2πr
v=
T
e da velocidade de translação,
GM
v=
r
GM 2πr
temos: =
r T
Elevando ambos os membros ao quadrado,
vem:
2
 GM  2πr 
2
  =  
 r   T 
 
GM 4π 2 r 2
=
r T2
Finalmente, obtém-se a expressão da 3ª lei
de Kepler:
T 2 4π 2 r 2
=
r3 GM
A constante da 3ª lei de Kepler é dada por
4 π 2 /GM, onde M é a massa do corpo
central. No caso do sistema planetário, M é
a massa do Sol.
3