O documento descreve os conceitos fundamentais de estática de corpos rígidos, incluindo:
1) Forças são caracterizadas por ponto de aplicação, intensidade, direção e sentido.
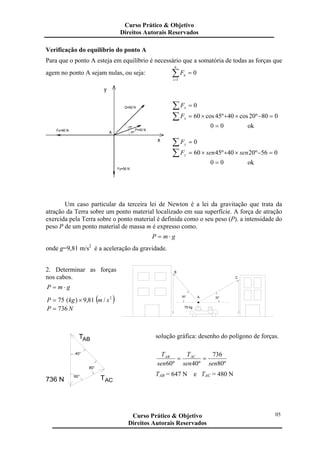
2) Um ponto está em equilíbrio quando a resultante de todas as forças que atuam nele é nula.
3) A resultante de um sistema de forças pode ser determinada graficamente ou analiticamente.