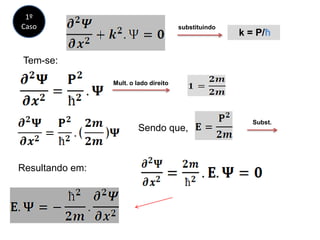
1) Erwin Schrödinger formulou a equação de onda, chamada Equação de Schrödinger, que descreve o comportamento de partículas subatômicas. 2) A Equação de Schrödinger surgiu da necessidade de conciliar a dualidade onda-partícula observada na física quântica. Ela relaciona a função de onda de uma partícula com a sua energia sob determinados potenciais. 3) A equação pode descrever tanto partículas livres quanto partículas sob a influência de um pot

1. Prof. Felipe de Almeida
UNIVERSIDADE FEDERAL RURAL DA AMAZÔNIA
GRADUAÇÃO EM ENGENHARIA AMBIENTAL e ENERGIAS
RENOVÁVEIS
Belém – Pará
2014
CIÊNCIA & TECNOLOGIA DE MATERIAIS

2. Equação de Schrödinger

3. Erwin Rudolf Josef Alexander Schrödinger
 Nasceu em 12 de agosto de 1887, em Viena;
 Físico da área de Física Quântica;
 Em 1933, em Oxford, juntamente com Paul Dirac,
ganhou o Prêmio Nobel pela formulação da equação
de onda chamada Equação de Schrödinger ;
 Participou da 1ª Guerra Mundial como oficial
de artilharia;

4. • Max Planck – Radiação de corpo Negro:
- “A energia é quantizada e não contínua”.
E = h.ν = h.ω/2π = h/2π.ω = ħ.ω
Assim,
E = ħ.ω ou ω = E/ħ
• Albert Einstein – Efeito Fotoelétrico:
- “A luz, onda eletromagnética, é formada por pequenas partículas, ‘quantum de
luz’, os fótons”.
E = h. ν = ħ.ω (energia do fóton)
Pela Teoria da Relatividade, temos que para uma partícula sem massa de
repouso (fótons):
P = E/ c (momento de p. sem massa)
Demonstração da equação de Schrödinger

5. Sendo E = h. ν e c = λ. ν, temos:
P = E/c = h.ν/λ.ν = h/2π/k = h/2π/k = ħ.k
Assim,
P = ħ.k ou k = P/ħ k é o n° de onda
Em resumo:
“A luz seria ENERGIA de caráter ondulatório (λ) e formada por partículas,
matéria, representada pelo momento (P) e também MATÉRIA com a mesma
característica dual”.
Teoria incompreendida por Schrödinger, o que o levou a
formulação da famosa Mecânica Ondulatória.

6.  Função de onda:
- Derivando em t: - Derivando em x:
então:ou
Antes da Equação de Schrödinger avaliemos que:
Parte-se a partir dessa equação.

7. k = P/ħ
substituindo
Tem-se:
Mult. o lado direito
Sendo que,
Subst.
Resultando em:
1º
Caso

8. Se,
lembre-se de que,
Então, substituindo no lado esquerdo, tem-se que:
Equação de Schrödinger
para partícula livre.
2º
Caso
Em sistemas conservativos, as partículas estão sujeitas
a um dado Potencial de energia.

9. Potencial de uma partícula
numa dada trajetória
n
Índice de refração de um raio
de luz numa dada trajetória
Sendo, Então o número de onda é dado por:
Substituindo esses valores, na equação de partida anterior, é dado:
Subst. n e

10. Mult.
Tem-se:
Multiplicando a EQ. anterior por,
x
Lembre:
com

11. Finalmente:
Equação de Schrödinger para uma partícula
sob um potencial V qualquer.