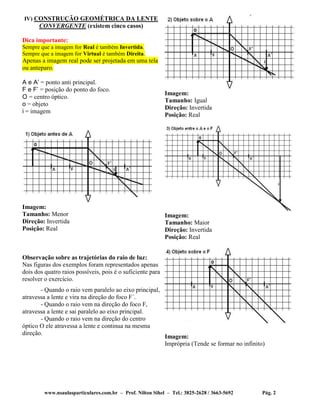
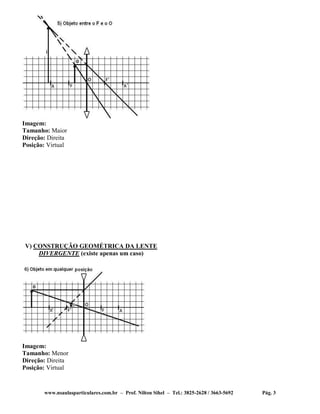
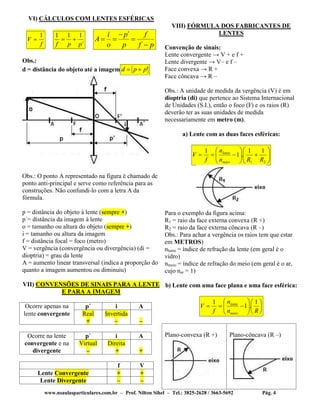
1) O documento discute os tipos e comportamento óptico de lentes esféricas, incluindo lentes convergentes e divergentes. 2) É apresentada a construção geométrica de lentes convergentes e divergentes, mostrando como cada uma forma imagens. 3) Instrumentos óticos como máquinas fotográficas, projetores, lupas e microscópios são explicados com base no comportamento das lentes.

1. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 1
LENTES ESFÉRICAS
I) TIPOS DE LENTES
Lentes de bordos
delgados:
Lentes de bordos
espessos:
II) REPRESENTAÇÃO DAS LENTES
Lentes Convergentes: Lentes Divergentes:
III) COMPORTAMENTO ÓPTICO
Sendo n1 = índice de refração do meio e
n2 = índice de refração da lente
Lentes Convergentes:
n2 > n1
n2 < n1
Lentes Divergentes:
n2 < n1
n2 > n1

2. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 2
IV) CONSTRUÇÃO GEOMÉTRICA DA LENTE
CONVERGENTE (existem cinco casos)
Dica importante:
Sempre que a imagem for Real é também Invertida.
Sempre que a imagem for Virtual é também Direita.
Apenas a imagem real pode ser projetada em uma tela
ou anteparo.
A e A’ = ponto anti principal.
F e F’ = posição do ponto do foco.
O = centro óptico.
o = objeto
i = imagem
Imagem:
Tamanho: Menor
Direção: Invertida
Posição: Real
Observação sobre as trajetórias do raio de luz:
Nas figuras dos exemplos foram representados apenas
dois dos quatro raios possíveis, pois é o suficiente para
resolver o exercício.
- Quando o raio vem paralelo ao eixo principal,
atravessa a lente e vira na direção do foco F´.
- Quando o raio vem na direção do foco F,
atravessa a lente e sai paralelo ao eixo principal.
- Quando o raio vem na direção do centro
óptico O ele atravessa a lente e continua na mesma
direção.
Imagem:
Tamanho: Igual
Direção: Invertida
Posição: Real
Imagem:
Tamanho: Maior
Direção: Invertida
Posição: Real
Imagem:
Imprópria (Tende se formar no infinito)

3. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 3
Imagem:
Tamanho: Maior
Direção: Direita
Posição: Virtual
V) CONSTRUÇÃO GEOMÉTRICA DA LENTE
DIVERGENTE (existe apenas um caso)
Imagem:
Tamanho: Menor
Direção: Direita
Posição: Virtual

4. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 4
VI) CÁLCULOS COM LENTES ESFÉRICAS
f
V
1

´
111
ppf

´i p f
A
o p f p

  

Obs.:
d = distância do objeto até a imagem 'ppd 
Obs.: O ponto A representado na figura é chamado de
ponto anti-principal e serve como referência para as
construções. Não confundi-lo com a letra A da
fórmula.
p = distância do objeto à lente (sempre +)
p´= distância da imagem à lente
o = tamanho ou altura do objeto (sempre +)
i = tamanho ou altura da imagem
f = distância focal = foco (metro)
V = vergência (convergência ou divergência) (di =
dioptria) = grau da lente
A = aumento linear transversal (indica a proporção do
quanto a imagem aumentou ou diminuiu)
VII) CONVENSÕES DE SINAIS PARA A LENTE
E PARA A IMAGEM
Ocorre apenas na p´ i A
lente convergente Real
+
Invertida
– –
Ocorre na lente p´ i A
convergente e na
divergente
Virtual
–
Direita
+ +
f V
Lente Convergente + +
Lente Divergente – –
VIII) FÓRMULA DOS FABRICANTES DE
LENTES
Convenção de sinais:
Lente convergente → V + e f +
Lente divergente → V– e f –
Face convexa → R +
Face côncava → R –
Obs.: A unidade de medida da vergência (V) é em
dioptria (di) que pertence ao Sistema Internacional
de Unidades (S.I.), então o foco (F) e os raios (R)
deverão ter as suas unidades de medida
necessariamente em metro (m).
a) Lente com as duas faces esféricas:













21
11
.1
1
RRn
n
f
V
meio
lente
Para o exemplo da figura acima:
R1 = raio da face externa convexa (R +)
R2 = raio da face externa côncava (R –)
Obs.: Para achar a vergência os raios tem que estar
em METROS)
nlente = índice de refração da lente (em geral é o
vidro)
nmeio = índice de refração do meio (em geral é o ar,
cujo nar = 1)
b) Lente com uma face plana e uma face esférica:













Rn
n
f
V
meio
lente 1
.1
1
Plano-convexa (R +) Plano-côncava (R –)

5. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 5
IX) ASSOCIAÇÃO DE LENTES = LENTES
JUSTAPOSTAS
É a lente equivalente da associação de duas lentes
justapostas. Sua vergência resultente V é igual a soma
algébrica das vergências das lentes associadas.
21 VVV 
X) INSTRUMENTOS ÓPTICOS
1) Máquina fotográfica: Como o objeto está muito
afastado da lente, a imagem fica real, invertida e
menor.
2) Projetor (slide, filmes, datashow): O objeto se
encontra entre o ponto anti principal e o foco,
formando assim uma imagem real, maior e
invertida.
f
V
1

´
111
ppf

pf
f
p
p
o
i
A


´
Atenção para a convenção de sinal
Lembre-se: apenas uma imagem real pode ser
projetada em uma tela ou anteparo.
3) Lupa ou lente de aumento:
Quando usada como lente de
aumento, a lupa tem a configuração
abaixo, formando uma imagem
virtual, direita e maior.
f
V
1

´
111
ppf

pf
f
p
p
o
i
A


´
Atenção para a convenção de sinal
Porém, se colocada na frente de um objeto
luminoso, pode servir como uma lente de uma
máquina fotográfica ou de um projetor de slide
(observe os exemplos 1 e 2).
É usada também para queimar objetos, pois os raios
solares vem de muito longe e paralelos, ao passar
pela lente, convergem para o foco. Como tem muita
luz (energia) concentrado em um único ponto, gera
calor.

6. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 6
4) Microscópio composto: É o aparelho óptico
constituído pela associação de duas lentes
convergentes.
A lente objetiva é a lente que está mais próxima do
objeto, fornecendo deste a primeira imagem.
A lente ocular situa próxima do olho do observador,
fornecendo a imagem final do sistema.
21´ ppd 
d= distância
entre as
lentes
ocularobjetiva AA
o
i
A  2
A = Aumento linear
transversal do
microscópio
1
1
1
f
V 
111 ´
111
ppf

11
1
1
1
1
1 ´
pf
f
p
p
o
i
Aobjetiva


2
2
1
f
V 
222 ´
111
ppf

22
2
2
2
1
2 ´
pf
f
p
p
i
i
Aocular


Esquema do Microscópio Composto
p1 = distância do objeto até a lente objetiva.
p1´= distância da imagem 1 até a lente objetiva (+)
p2 = distância da imagem 1 até a lente ocular (+)
(para a lente ocular, a imagem 1 equivale ao seu
objeto)
p2´= distância da imagem 2 até a lente ocular (-) (é
negativa pois esta segunda imagem é virtual)
o = tamanho do objeto
i1 = tamanho da imagem 1 (é negativa em relação à
lente objetiva e positiva em relação à lente ocular)
i2 = tamanho da imagem 2 que será vista pelo
observador. (+)
d = distância entre a lente objetiva e a ocular.
f1 = foco da lente objetiva
f2 = foco da lente ocular
A = aumento linear transversal (-)
Aobjetiva = aumento linear transversal da lente
objetiva (-)
Aocular = aumento linear transversal da lente ocular
(+)
5) Luneta
2
1
f
f
G 
21 pfd 
2
2
1
f
V 
G = aumento visual de uma luneta
f1 = foco da lente objetiva
f2 = foco da lente ocular
d = distância entre as lentes
i1 = tamanho da imagem 1 (é
negativa em relação à lente objetiva
e positiva em relação à lente ocular)
i2 = tamanho da imagem 2 que será
vista pelo observador. (+)
p2 = distância da imagem 1 até a
lente ocular (+) (para a lente ocular,
a imagem 1 equivale ao seu objeto)
p2´= distância da imagem 2 até a
lente ocular (-) (é negativo pois esta
segunda imagem é virtual)
222 ´
111
ppf

22
2
2
2
1
2 ´
pf
f
p
p
i
i
Aocular



7. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 7
XI) DEFEITOS DA VISÃO
1) Miopia: Ocorre com pessoas que tem dificuldade
em ver com nitidez imagens muito longe.
A imagem se forma antes da retina, o que faz com que
a pessoa veja uma imagem embaçada, sem nitidez.
Sua correção é feita com lente divergente, que
aproxima a imagem do olho.
Está cada vez mais freqüente em razão da
hereditariedade e da ação do meio ambiente.
O seu foco é igual ao valor do ponto remoto (pR),
porém, como é uma lente divergente, seu valor é
negativo. A unidade de medida tem que ser o metro.
Ponto remoto é a posição de um objeto que está
muito afastado do olho.
Rpf 
f
V
1

A vergência é o grau do óculos. Como
o foco está em metros (m), a
vergência é dada em dioptrias (di), ou
seja, -5di equivale a uma lente
divergente de 5º
A miopia pode ser corrigida através da cirurgia a laser,
onde se aumenta o raio de curvatura do cristalino
mudando assim o seu foco.
2) Hipermetropia e Presbiopia (vista cansada):
Ocorre com pessoas que tem dificuldade em ver com
nitidez imagens muito perto.
A imagem se forma depois (atrás) da retina, o que faz
com que a pessoa veja uma imagem embaçada, sem
nitidez. Com a idade, a visão se torna cada vez mais
embaçada. Sua correção é feita com lente
convergente, que afasta a imagem do olho até o valor
do ponto próximo de um olho saudável.
pp é o ponto próximo da pessoa com hipermetropia.
Na fórmula aparece o sinal negatio pois é uma
imagem virtual, semelhante a da lente de aumento.
Ponto próximo é o ponto mais próximo do olho
para se ver com nitidez. Seu valor, em geral, é de 25
cm ou 0,25 m para um olho saudável.
ppf
V
1
25,0
11

Como se trata de uma lente
convergente, sua vergência
(em dioptrias) e seu foco
(em metros) são
considerados positivos. Assim uma lente de +5di
equivale a uma lente convergente de 5º.
A hipermetropia pode ser corrigida através da
cirurgia a laser, onde modifica-se a curvatura da
córnea para a imagem ser projetada na retina.