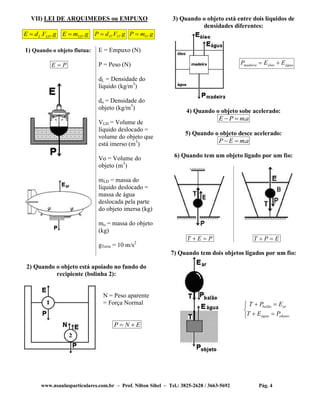
1) O documento apresenta os principais conceitos de hidrostática, incluindo densidade, massa específica, volume, pressão, teorema de Stevin sobre pressão de líquidos, tubos em U, princípio de Pascal e lei de Arquimedes. 2) São definidas equações para calcular densidade, massa específica, pressão, pressão de líquidos em função da altura e volume de objetos geométricos como prisma, cilindro, paralelepípedo e esfera. 3) Exemplos ilustram a var

1. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 1
HIDROSTÁTICA
I) DENSIDADE
TV
m
d 
II) MASSA ESPECÍFICA
MV
m

VM = VT – Vvazio (oco)
Obs.: Quando o objeto for
maciço, d = µ
CÁLCULO DO VOLUME:
Prisma e Cilindro
Volume = Área da base x altura
Área do círculo: A =  . r2
Paralelepípedo
Volume = comprim. x larg. x alt.
Cubo
Volume = lado3
Esfera
3
3
4
RV 
d = Densidade
(kg/m3
; kg/; g/cm3
)
VT = Volume total do
objeto
(m3
; cm3
;  = litro)
m = Massa (Kg ; g)
 = Massa específica
(kg/m3
; kg/; g/cm3
)
VM = Volume só do
material
(m3
; cm3
;  = litro)
Lembrando que:
1 g/cm3
= 1.000 kg/m3
1 kg/ = 1.000 kg/m3
1 m3
= 1.000 
1 kg = 1.000 g
1 m = 100 cm
1 m2
= 10.000 cm2
1 m3
= 1.000.000 cm3
III) PRESSÃO
A
F
p 
P = pressão
[N/m2
= Pa (pascal)]
F = Força (N)
A = área (m2
)
Observações importantes:
Nas figuras a seguir a força é a mesma, porém a
pressão não. Quanto menor a área, maior será a
pressão.
1)
pressão I < pressão II < pressão III
Peso I = Peso II = Peso III
2)
pressão I > pressão II
Peso I = Peso II
3)
pressão na ponta da tachinha > pressão na cabeça da ta chinha
Força na ponta da tachinha = Força na cabeça da tachinha

2. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 2
IV) TEOREMA DE STEVIN ou
PRESSÃO DE UM LÍQUIDO
A pressão de um líquido é diretamente
proporcional à altura dele. Quanto maior a
profundidade, maior será a pressão no fundo.
hgdpliq ..
atmphgdp  ..
g = 10 m/s2
plíq = Pressão do líquido ou
pressão hidrostática
p = Pressão ou Pressão total
[N/m2
= Pa (pascal)]
patm = Pressão atmosférica = 1
atm  105
N/m2
d = densidade do líquido (kg/m3
)
h = altura (m)
atmA pp 
11 .. hgdpp atmB 
2211 .... hgdhgdpp atmC 
332211 ...... hgdhgdhgdpp atmD 
Observações importantes:
Observe a diferença dos jatos pelo nível de água.
Quanto maior a altura da coluna de água, maior
será a pressão.
Na garrafa com tampa
a pressão do ar impede
a saída de água pelo
primeiro furo:
Note que para líquidos diferentes a densidade
modifica a
inclinação do
gráfico da
pressão:
Barragem: Note que
na parte de baixo a
barragem deve ser
mais larga pois tem
maior pressão:
Independente do formato das garrafas, a pressão
no fundo é igual para todas, pois, considerando
sempre o
mesmo
líquido, a
pressão
depende da
altura.
V) TUBO EM U ou
VASOS COMUNICANTES
1) Tubo aberto dos dois lados:
Obs.: Traçar uma linha horizontal passando pelo
ponto mais baixo que separa os dois líquidos.
A B
p p

atmliqliqatmliq ppppp  321

1 2 3liq liq liq
p p p 

1 1 2 2 3 3
d gh d gh d gh 

332211 ... hdhdhd 

3. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 3
2) Tubo fechado de um dos lados:
Obs.: Traçar uma linha horizontal passando pelo
ponto mais baixo que separa o líquido do gás.
a) Quando o líquido no tubo é o MERCÚRIO, a
própria altura da coluna de Hg (mercúrio) é
considerado a pressão.
A B
p p

gás liq atm
p p p 

cmHgoummHgematmliqgás php 
Neste exemplo:
Pgás = 150 mmHg + 760 mmHg = 910 mmHg
Patm = 76 cmHg = 760 mmHg = 1 atm
(pgás com unidades em mmHg ou cmHg)
b) Quando é dado um líquido qualquer no tubo:
A B
p p

gás liq atm
p p p 

atmgás phgdp  ..
Observação:
Mangueira de
plástico
transparente para
usar como nível
em obra através
do nível da água.
O conta gotas permite o
líquido subir pois a pressão do
gás no seu interior fica menor
que a pressão atmosférica
VI) PRINCÍPIO DE PASCAL ou PRENSA
HIDRÁULICA
21 pp 
2
2
1
1
A
F
A
F

V1 = V2
2211 .. hAhA 
2
.rAcírculo 
p = pressão
(N/m2
= Pa)
F = Força (N)
A = área do
êmbolo (círculo)
(m2
)
h = altura
deslocada pelo
êmbolo (m)
r = raio do
círculo do
êmbolo
F1 < F2 < F3 < F4
p1 = p2 = p3 = p4

4. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 4
VII) LEI DE ARQUIMEDES ou EMPUXO
gVdE LDL .. gmE LD . gVdP OO .. gmP O .
1) Quando o objeto flutua:
PE 
E = Empuxo (N)
P = Peso (N)
dL = Densidade do
líquido (kg/m3
)
do = Densidade do
objeto (kg/m3
)
VLD = Volume de
líquido deslocado =
volume do objeto que
está imerso (m3
)
Vo = Volume do
objeto (m3
)
mLD = massa do
líquido deslocado =
massa de água
deslocada pela parte
do objeto imersa (kg)
mo = massa do objeto
(kg)
gTerra = 10 m/s2
2) Quando o objeto está apoiado no fundo do
recipiente (bolinha 2):
N = Peso aparente
= Força Normal
ENP 
3) Quando o objeto está entre dois líquidos de
densidades diferentes:
águaóleomadeira EEP 
4) Quando o objeto sobe acelerado:
amPE .
5) Quando o objeto desce acelerado:
amEP .
6) Quando tem um objeto ligado por um fio:
PET  EPT 
7) Quando tem dois objetos ligados por um fio:





objetoágua
arbalão
PET
EPT