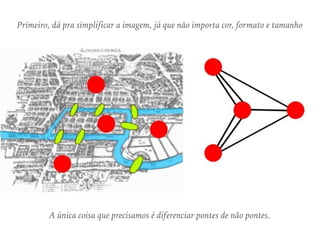
1) A teoria dos grafos surgiu a partir do problema das sete pontes de Königsberg na Alemanha no século 18. 2) Euler resolveu o problema ao modelá-lo matematicamente usando vértices e arestas, fundando assim a teoria dos grafos. 3) Grafos podem ser usados para modelar diversos sistemas reais como redes de transporte, relações sociais em redes sociais.

1. TEORIA DOS GRAFOS
Victor Hazin da Rocha

2. ORIGEM DA
TEORIA DOS
GRAFOS
“As 7 pontes de Konigsberg”

3. AS SETE PONTES DE KONIGSBERG
Na cidade de Konigsberg,
Alemanha, um rio passava pela
cidade e a dividia em quatro
partes. Para interligar estas
partes, haviam sete pontes.
Dada a situação ilustrada na
imagem, é possível (passando só
uma vez por cada ponte) fazer
um caminho que passe por todas
elas?

5. É impossível traçar um caminho
que passe só uma vez por cada
ponte e, no final, tenha
atravessado todas elas!

6. No entanto, se o número de
pontes fosse, digamos, seis,
haveria tal caminho.
O caminho exibido é hoje
chamado de Caminho Euleriano.

7. EULER “O FILHO DO VENTO”
Para mostrar que era impossível
responder que sim ao problema,
Euler fundou uma área da
Matemática que se chama Teoria
dos Grafos, que é um modelo
cujas preocupações estão nas
relações entre pares de
entidades.

8. EULER
(O original)

9. A única coisa que precisamos é diferenciar pontes de não pontes.
Primeiro, dá pra simplificar a imagem, já que não importa cor, formato e tamanho

10. ➤ Vamos chamar as pontes de
arestas e o que não são pontes
de vértices, dessa forma o
problema se torna mais
genérico.
➤ O grau de um vértice é a
quantidade de arestas que se
conectam a ele.
➤ Todo vértice vai ter um rótulo
único(nesse caso uma letra)
que o representa, o mesmo
vale para arestas (números).

11. ➤ Neste grafo, cada vértice tem
grau ÍMPAR.
➤ Os vértices A, B e D têm a
mesma quantidade de arestas,
três. C tem cinco.
➤ Se você parte de um vértice
com um número ímpar de
arestas, você estará condenado
a não terminar nele, caso
queira percorrer todas as
arestas só uma vez.

12. ➤ Se tenho três arestas. Saio por
uma, restam duas. Volto por
outra, sobra uma. Saio pela
última. Não consigo mais voltar
a este vértice, respeitando as
condições impostas.
➤ Se começo fora de um vértice V,
e V tem número ímpar de
arestas, o que acontece?
Mesmo raciocínio.
➤ Podemos então concluir que
um vértice com grau ímpar
deve ser onde começa ou
termina nosso caminho.

13. ➤ Podemos então concluir que
um vértice com grau ímpar
deve ser onde começa ou
termina nosso caminho.
➤ Para o caso das pontes de
Konigsberg, há quatro vértices
de grau ímpar.
➤ Mas já vimos que tais vértices
devem estar no início ou no
fim (e só há um início e um
fim)

14. ➤ Mas já vimos que tais vértices
devem estar no início ou no
fim (e só há um início e um
fim)
➤ Portanto, podemos ter no
máximo dois vértices de grau
ímpar para resolver o
problema. Acho que
concordamos que 4 > 2.
Assim, é impossível traçar tal
caminho, nas condições dadas.

15. ALGUMAS
APLICAÇÕES
DE GRAFOS

16. REDES DE TRANSPORTE
➤ Podemos modelar uma rede de
transporte com grafo.
➤ Vamos supor que estamos
interessados na conectividade entre
um grupo de cidades.
➤ Os vértices podem ser as cidades (ex:
São Paulo, Campinas, Ribeirão Preto,
etc).
➤ Já as arestas, podem ser
simplesmente a conexão direta entre
duas cidades.
➤ Você ainda poderia dizer que as
arestas guardam as distâncias duma
cidade até outra (aí já entra o conceito
de grafo ponderado, isto é, com peso
nos vértices e/ou arestas).

17. AMIGOS NO FACEBOOK
➤ Os nós são os “perfis”.
➤ As arestas são as relações de
amizade"

18. TEORIA DOS
GRAFOS
conceitos

19. “A teoria dos grafos é um ramo da matemática que estuda
as relações entre os objetos de um determinado conjunto.
Para tal são empregadas estruturas chamadas de GRAFOS,

20. “Um grafo é uma estrutura abstrata que representa um
conjunto de elementos denominados vértices e suas
relações de interdependência ou arestas.

21. “Um grafo G(V,A) é definido pelo par de conjuntos V e A,
onde:
V é conjunto não vazio: os vértices ou nós do grafo;
A é conjunto de pares ordenados a=(v,w), v e w ∈ V:
as arestas do grafo
definição matemática

22. Seja, por exemplo, o grafo G(V,A)
dado por:
V = { p | p é uma pessoa }
A = { (v,w) | < v é amigo de w > }
Esta definição representa toda uma
família de grafos.
Um exemplo de elemento desta
família é dado por:
V = { Maria, Pedro, Joana, Luiz }
A = { (Maria, Pedro), (Pedro,
Maria), (Joana, Maria), (Maria,
Joana), (Pedro, Luiz), (Luiz, Pedro),
(Joana, Pedro) , (Pedro, Joana) }
*Neste exemplo estamos considerando que a relação <v é amigo de w> é
uma relação simétrica, ou seja, se <v é amigo de w> então <w é amigo
de v>. Como conseqüência, as arestas que ligam os vértices não possuem
qualquer orientação
Maria
Pedro
Joana Luiz
G1

23. DÍGRAFO (GRAFO ORIENTADO)
Considere, agora, o grafo
definido por:
V = { p | p é uma pessoa da família
Castro }
A = { (v,w) | < v é pai/mãe de w > }
Um exemplo de deste grafo é:
V = { Emerson, Isadora, Renata,
Antonio, Cecília, Alfredo }
A = {(Isadora, Emerson),
(Antonio, Renata), (Alfredo,
Emerson), (Cecília, Antonio),
(Alfredo, Antonio)}
Renata
Emerson
Antonio
Cecília
Alfredo
Isadora
G2

24. DÍGRAFO (GRAFO ORIENTADO)
A relação definida por A não é
simétrica;
pois se <v é pai/mãe de w>, não
é o caso de <w é pai/mãe de v>.
Há, portanto, uma orientação na
relação, com um correspondente
efeito na representação gráfica de
G.
Esse grafo é dito ser um grafo
orientado (ou dígrafo), sendo
que as conexões entre os vértices
são chamadas de arcos.
Renata
Emerson
Antonio
Cecília
Alfredo
Isadora
G2

25. GRAFO COMPLETO
➤ Um grafo completo com v vértices, escrito Kv, é um grafo
simples onde todo par de vértices é ligado por uma aresta.
➤ Em outras palavras, um grafo completo é um grafo simples
que contém o número máximo de arestas.

26. SUBGRAFO
➤ Um grafo G2(V2,E2) é um subgrafo de
um grafo G1(V1,E1) se:
➤ V2 ⊆ V1;
➤ E2 ⊆ E1.
➤ Podemos verificar facilmente os
seguintes enunciados:
➤ Todo grafo é subgrafo dele
mesmo.
➤ O subgrafo de um subgrafo de
G é um subgrafo de G.
➤ Um vértice de G é um subgrafo
de G.
➤ Um aresta de G com os dois
vértices que ele liga é um
subgrafos de G.
G1

27. SUBGRAFO
➤ Um grafo G2(V2,E2) é um subgrafo de
um grafo G1(V1,E1) se:
➤ V2 ⊆ V1;
➤ E2 ⊆ E1.
➤ Podemos verificar facilmente os
seguintes enunciados:
➤ Todo grafo é subgrafo dele
mesmo.
➤ O subgrafo de um subgrafo de
G é um subgrafo de G.
➤ Um vértice de G é um subgrafo
de G.
➤ Um aresta de G com os dois
vértices que ele liga é um
subgrafos de G.
G1
G2

28. SUBGRAFOS
➤ Clique: Uma clique é um subgrafo que é completo.
➤ Subgrafo induzido: Seja H(W,F) um subgrafo de G = (V,E).
Se uma aresta entre dois vértices de W existe se e somente se
essa aresta existe em V, digamos que H é um subgrafo
induzido por W.
➤ Conjunto independente de vértices: Um subgrafo induzido
de G que não contém nenhuma aresta.

29. ADJACÊNCIA
➤ Em um grafo simples (G1)
dois vértices v e w são
adjacentes (ou vizinhos) se há
uma aresta a=(v,w) em G.
➤ Está aresta é dita ser incidente
a ambos, v e w.
➤ É o caso dos vértices Maria
e Pedro em G1.
Maria
Pedro
Joana Luiz
G1

30. ADJACÊNCIA
➤ No caso do grafo ser dirigido (G2),
a adjacência(vizinhança) é
especializada em:
➤ Sucessor: um vértice w é sucessor
de v se há um arco que parte de v e
chega em w.
➤ Em G2, por exemplo, diz-se que
Emerson e Antonio são
sucessores de Alfredo.
➤ Antecessor: um vértice v é
antecessor de w se há um arco que
parte de v e chega em w.
➤ Em G2, por exemplo, diz-se que
Alfredo e Cecília são
antecessores de Antonio.
Renata
Emerson
Antonio
Cecília
Alfredo
Isadora
G2

31. ORDEM
➤ A ordem de um grafo G é dada pela cardinalidade do conjunto
de vértices, ou seja, pelo número de vértices de G.
Ordem = 4
Ordem = 6
Maria
Pedro
Joana Luiz
G1
Renata
Emerson
Antonio
Cecília
Alfredo
Isadora
G2

32. GRAU
➤ O grau de um vértice é dado
pelo número de arestas que
lhe são incidentes.
➤ Em G1, por exemplo:
➤ grau(Pedro) = 3
➤ grau(Maria) = 2
Maria
Pedro
Joana Luiz
G1

33. GRAU
➤ No caso do grafo ser dirigido (G2), a
noção de grau é especializada em:
➤ Grau de emissão: o grau de emissão
de um vértice v corresponde ao
número de arcos que partem de v.
➤ grauDeEmissão(Antonio) = 1
➤ grauDeEmissao(Alfredo) = 2
➤ grauDeEmissao(Renata) = 0
➤ Grau de recepção: o grau de
recepção de um vértice v corresponde
ao número de arcos que chegam a v.
➤ grauDeRecepção(Antonio) = 2
➤ grauDeRecepção(Alfredo) = 0
➤ grauDeRecepção(Renata) = 1
Renata
Emerson
Antonio
Cecília
Alfredo
Isadora
G2

34. FONTE
➤ Um vértice v é uma fonte se
grauDeRecepção(v) = 0.
➤ É o caso dos vértices Isadora,
Alfredo e Cecília em G2.
Renata
Emerson
Antonio
Cecília
Alfredo
Isadora
G2

35. SUMIDOURO
➤ Um vértice v é um sumidouro
se grauDeEmissão(v) = 0.
➤ É o caso dos vértices Renata e
Emerson em G2.
Renata
Emerson
Antonio
Cecília
Alfredo
Isadora
G2

36. LAÇO
➤ Um laço é uma aresta ou arco
do tipo a=(v,v), ou seja, que
relaciona um vértice a ele
próprio.
➤ Em G3 há três ocorrências de
laços para um grafo não
orientado.C
A B
D
G3

37. GRAFO REGULAR
➤ Um grafo é dito ser regular quando todos os seus vértices tem
o mesmo grau.

38. GRAFO BIPARTIDO
➤ Um grafo é dito ser bipartido
quando seu conjunto de
vértices V puder ser
particionado em dois
subconjuntos V1 e V2, tais que
toda aresta de G une um
vértice de V1 a outro de V2.
H={h | h é um homem}
M={m | m é um mulher}
MuMaria CarlaJoana
LuizPedro H
M
G(V,A) é um grafo onde:
V = H U M
A = {(v,w) | (v ∈ H e w ∈ M) ou (v ∈ M e w ∈ H)
e <v foi namorado de w>}

39. GRAFO BIPARTIDO COMPLETO
➤ Um grafo é dito ser bipartido
completo quando todos os
vértices de uma partição estão
ligados a todos os vértices da
outra partição.
MuMaria CarlaJoana
LuizPedro

40. GRAFO ROTULADO
➤ Um grafo G(V,A) é dito ser
rotulado em vértices (ou
arestas) quando a cada vértice
(ou aresta) estiver associado
um rótulo.
Maria CarlaJoana
LuizPedro

41. GRAFO VALORADO
➤ Um grafo G(V,A) é dito ser
valorado quando existe uma
ou mais funções relacionando
V e/ou A com um conjunto de
números.
➤ Seja G(V,A) onde:
➤ V = {v | v é uma cidade
com aeroporto}
➤ A = {(v,w,t) | <há linha
aérea ligando v a w, sendo t
o tempo esperado de voo>}
Sao
Paulo
Curitiba
Recife
Porto
Alegre
20
12060
150

42. MULTIGRAFO
➤ Um grafo G(V,A) é dito ser
um multigrafo quando
existem múltiplas arestas
entre pares de vértices de G.
➤ No exemplo, há duas arestas
entre os vértices São Paulo e
Curitiba e entre os vértices
Curitiba e Recife,
caracterizando-o como um
multigrafo.
Sao
Paulo
Recife
Porto
Alegre
Curitiba

43. HIPERGRAFO
➤ Um hipergrafo é uma
generalização de um grafo,
com suas arestas ligando
quaisquer quantidades
positivas de vértices.
➤ Um hipergrafo H(V,A) é
definido pelo par de conjuntos
V e A, onde:
➤ V - conjunto não vazio;
➤ A - uma família e partes não
vazias de V.
Maria
Pedro
Joana Luiz

44. CADEIA
➤ Uma cadeia é uma sequência qualquer
de arestas adjacentes que ligam dois
vértices.
➤ O conceito de cadeia vale também para
grafos orientados, bastando que se
ignore o sentido da orientação dos
arcos.
➤ Uma cadeia é dita ser elementar se não
passa duas vezes pelo mesmo vértice.
➤ É dita ser simples se não passa duas
vezes pela mesma aresta (arco).
➤ O comprimento de uma cadeia é o
número de arestas (arcos) que a
compõe.
➤ A seqüência de vértices (x6, x5, x4, x1)
é um exemplo de cadeia
x1
x6x3
x2 x5
x4

45. CAMINHO
➤ Um caminho é uma cadeia na
qual todos os arcos possuem a
mesma orientação. Aplica-se,
portanto, somente a grafos
orientados.
➤ A seqüência de vértices (x1,
x2, x5, x6, x3) é um exemplo
de caminho.
x1
x6x3
x2 x5
x4

46. CICLO
➤ Um ciclo é uma cadeia simples
e fechada (o vértice inicial é o
mesmo que o vértice final).
➤ A seqüência de vértices (x1,
x2, x3, x6, x5, x4, x1) é um
exemplo de ciclo elementar.
x1
x6x3
x2 x5
x4

47. CIRCUITO
➤ Um circuito é um caminho
simples e fechado.
➤ A seqüência de vértices (x1,
x2, x5, x4, x1) é um exemplo
de circuito elementar.
x1
x6x3
x2 x5
x4

48. FECHO TRANSITIVO
➤ O fecho transitivo direto
(FTD) de um vértice v é o
conjunto de todos os vértices
que podem ser atingidos por
algum caminho iniciando em
v.
➤ O FTD do vértice x5 do grafo
é o conjunto: {x1, x2, x3, x4,
x5, x6}.
➤ Note que o próprio vértice faz
parte do FTD já que ele é
alcançável partindo-se dele
mesmo.
x1
x6x3
x2 x5
x4
x7

49. FECHO TRANSITIVO
➤ O fecho transitivo inverso
(FTI) de um vértice v é o
conjunto de todos os vértices a
partir dos quais se pode
atingir v por algum caminho.
➤ O FTI do vértice x5 do grafo é
o conjunto: {x1, x2, x4, x5,
x7}.
➤ Note que o próprio vértice faz
parte do FTI já que dele se
pode alcançar ele mesmo.
x1
x6x3
x2 x5
x4
x7

50. GRAFO CONEXO
➤ Um grafo G(V,A) é dito ser
conexo se há pelo menos uma
cadeia ligando cada par de
vértices deste grafo G.
x1
x6x3
x2 x5
x4

51. GRAFO DESCONEXO
➤ Um grafo G(V,A) é dito ser
desconexo se há pelo menos
um par de vértices que não
está ligado por nenhuma
cadeia.
x1
x6x3
x2 x5
x4

52. COMPONENTE CONEXA
➤ Um grafo G(V,A) desconexo é
formado por pelo menos dois
subgrafos conexos, disjuntos
em relação aos vértices e
maximais em relação à
inclusão.
➤ Cada um destes subgrafos
conexos é disto ser uma
componente conexa de G.
x6
x5
x1
x3
x2
x4

53. GRAFO FORTEMENTE CONEXO
➤ No caso de grafos orientados,
um grafo é dito ser fortemente
conexo (f-conexo) se todo par
de vértices está ligado por pelo
menos um caminho em cada
sentido, ou seja, se cada par de
vértices participa de um
circuito.
➤ Isto significa que cada vértice
pode ser alcançável partindo-
se de qualquer outro vértice
do grafo.
x1
x6x3
x2 x5
x4

54. COMPONENTE FORTEMENTE CONEXA
➤ Um grafo G(V,A) que náo é
fortemente conexo é formado
por pelo menos dois subgrafos
fortemente conexos, disjuntos
em relação aos vértices e
maximais em relação à
inclusão.
➤ Cada um destes subgrafos é
disto ser uma componente
fortemente conexa de G, a
exemplo dos subgrafos
identificados por S1, S2 e S3.
x1
x6x3
x2 x5
x4
x7
S3
S1
S2

55. VÉRTICE DE CORTE
➤ Um vértice é dito ser um
vértice de corte se sua
remoção (juntamente com as
arestas a ele conectadas)
provoca um redução na
conexidade do grafo.
➤ Os vértices x2 é um exemplos
de vértices de corte.
x1
x6x3
x2 x5
x4

56. PONTE
➤ Uma aresta é dita ser um a
ponte se sua remoção provoca
um redução na conexidade do
grafo.
➤ As arestas (x1, x2) são
exemplos de pontes.
x1
x3
x2
x4

57. BASE
➤ Uma base de um grafo G(V,A)
é um subconjunto B ⊆ V, tal
que:
➤ Dois vértices quaisquer de
B não são ligados por
nenhum caminho;
➤ Todo vértice não
pertencente a B pode ser
atingido por um caminho
partindo de B.
B1
B2
X1
X2
X3
A1
A2
A3
B
A

58. ANTI-BASE
➤ Uma anti-base de um grafo
G(V,A) é um subconjunto A ⊆
V, tal que:
➤ Dois vértices quaisquer de
A não são ligados por
nenhum caminho;
➤ De todo vértice não
pertencente a A pode ser
atingir A por um caminho.
B1
B2
X1
X2
X3
A1
A2
A3
B
A

59. RAIZ
➤ Se a base de um grafo
G(V,A) é um conjunto
unitário, então esta base é a
raiz de G.
B2
X2
X3
A1
A2
A3
B
A

60. ANTI-RAIZ
➤ Se a anti-base de um grafo
G(V,A) é um conjunto
unitário, então esta anti-base é
a anti-raiz de G.
B1
B2
X1
X2
X3
A3
B
A

61. ÁRVORE
➤ Uma árvore é um grafo conexo sem ciclos.
➤ Seja G(V,A) um grafo com ordem n ≥ 2.
As propriedades seguintes são
equivalentes e suficientes para caracterizar
G como uma árvore:
1. G é conexo e sem ciclos;
2. G é sem ciclos e tem n-1 arestas;
3. G é conexo e tem n-1 arestas;
4. G é sem ciclos e por adição de uma
aresta se cria um ciclo e somente um;
5. G é conexo, mas deixa de sê-lo se
uma aresta é suprimida (todas as
arestas são pontes);
6. Todo par de vértices de G é unido por
uma e somente uma cadeia simples.
X1
X2
X3
X4
X5
X6

62. ARBORESCÊNCIA
➤ Uma arborescência é uma
árvore que possui uma raiz.
➤ Aplica-se, portanto, somente a
grafos orientados.
X1
X2
X3
X4
X5
X6

63. FLORESTA
➤ Uma floresta é um grafo cujas
componentes conexas são
árvores.
X1
X2
X3
X4
X5
X6

64. GRAFO PLANAR
➤ Um grafo G(V,A) é dito ser
planar quando existe alguma
forma de se dispor seus
vértices em um plano de tal
modo que nenhum par de
arestas se cruze.

65. COLORAÇÃO
➤ Seja G(V,A) um grafo e C um
conjunto de cores.
➤ Uma coloração de G é uma
atribuição de alguma cor de C
para cada vértice de V, de tal
modo que a dois vértices
adjacentes sejam atribuídas cores
diferentes.
➤ Assim sendo, uma coloração de G
é uma função f:
➤ V → C tal que para cada par de
vértices (v,w) ∈ A → f(v) ≠
f(w).
➤ O exemplo ao lado mostra um
4-coloração para o grafo.

66. NÚMERO CROMÁTICO
➤ Denomina-se número
cromático X(G) de um grafo G
ao menor número de cores k,
para o qual existe uma k-
coloração de G.
➤ O exemplo ao lado mostra
uma 3-coloração para o grafo,
que é o número cromático
deste grafo.

67. ISOMORFISMO
➤ Sejam dois grafos G1(V1,A1) e
G2(V2,A2).
➤ Um isomorfismo de G1 sobre
G2 é um mapeamento bijetivo f:
➤ V1 ↔ V2
➤ Tal que (x,y) ∈ A1 se e
somente se (f(x),f(y)) ∈ A2,
para todo x,y ∈ V1.
➤ Os grafos ao lado são isomorfos
pois há a função { (a,2), (b,1),
(c,3), (d,4), (e,6), (f,5) } que
satisfaz a condição descrita
acima.
A
DE
F C
B
2
4
6
5 3
1

69. EXCENTRICIDADE
➤ A excentricidade ou Ex(v) de
um vértice v pertencente a G é
a maior distância entre v e w,
para todo w pertencente a G.
➤ Ela pode ser pensada como o
quanto um nó é distante do nó
mais distante dele no grafo.
V
W

70. EXCENTRICIDADE
➤ A excentricidade ou Ex(v) de
um vértice v pertencente a G é
a maior distância entre v e w,
para todo w pertencente a G.
➤ Ela pode ser pensada como o
quanto um nó é distante do nó
mais distante dele no grafo.
V
W

71. EXCENTRICIDADE
➤ A excentricidade ou Ex(v) de
um vértice v pertencente a G é
a maior distância entre v e w,
para todo w pertencente a G.
➤ Ela pode ser pensada como o
quanto um nó é distante do nó
mais distante dele no grafo.
V
W

72. EXCENTRICIDADE
➤ A excentricidade ou Ex(v) de
um vértice v pertencente a G é
a maior distância entre v e w,
para todo w pertencente a G.
➤ Ela pode ser pensada como o
quanto um nó é distante do nó
mais distante dele no grafo.
V
W

73. EXCENTRICIDADE
➤ A excentricidade ou Ex(v) de
um vértice v pertencente a G é
a maior distância entre v e w,
para todo w pertencente a G.
➤ Ela pode ser pensada como o
quanto um nó é distante do nó
mais distante dele no grafo.
➤ Observe que não existe outro
nós mais distante que w.
V
W
Ex(v) = 4

74. RAIO
➤ O raio de um grafo é a
excentricidade mínima de
qualquer vértice do grafo.
➤ É o menor valor de
excentricidade para todo
vertice v pertencente a um
grafo G.
v
w

75. RAIO
➤ O raio de um grafo é a
excentricidade mínima de
qualquer vértice do grafo.
➤ É o menor valor de
excentricidade para todo
vertice v pertencente a um
grafo G.
v
w

76. RAIO
➤ O raio de um grafo é a
excentricidade mínima de
qualquer vértice do grafo.
➤ É o menor valor de
excentricidade para todo
vertice v pertencente a um
grafo G.
v
w

77. RAIO
➤ O raio de um grafo é a
excentricidade mínima de
qualquer vértice do grafo.
➤ É o menor valor de
excentricidade para todo
vertice v pertencente a um
grafo G.
v
w
Rad(G) = 3

78. DIÂMETRO
➤ O diâmetro de um grafo é a
excentricidade máxima de
qualquer vértice do grafo.
➤ Ou seja, ele é a maior
distância entre qualquer par
de vértices. Para achar o
diâmetro de um grafo,
primeiro encontre o caminho
mínimo entre cada par de
vértices.
➤ O maior comprimento de
qualquer um desses caminhos
é o diâmetro do grafo.
V
W

79. DIÂMETRO
➤ O diâmetro de um grafo é a
excentricidade máxima de
qualquer vértice do grafo.
➤ Ou seja, ele é a maior
distância entre qualquer par
de vértices. Para achar o
diâmetro de um grafo,
primeiro encontre o caminho
mínimo entre cada par de
vértices.
➤ O maior comprimento de
qualquer um desses caminhos
é o diâmetro do grafo.
V
W

80. DIÂMETRO
➤ O diâmetro de um grafo é a
excentricidade máxima de
qualquer vértice do grafo.
➤ Ou seja, ele é a maior
distância entre qualquer par
de vértices. Para achar o
diâmetro de um grafo,
primeiro encontre o caminho
mínimo entre cada par de
vértices.
➤ O maior comprimento de
qualquer um desses caminhos
é o diâmetro do grafo.
V
W

81. DIÂMETRO
➤ O diâmetro de um grafo é a
excentricidade máxima de
qualquer vértice do grafo.
➤ Ou seja, ele é a maior
distância entre qualquer par
de vértices. Para achar o
diâmetro de um grafo,
primeiro encontre o caminho
mínimo entre cada par de
vértices.
➤ O maior comprimento de
qualquer um desses caminhos
é o diâmetro do grafo.
V
W

82. DIÂMETRO
➤ O diâmetro de um grafo é a
excentricidade máxima de
qualquer vértice do grafo.
➤ Ou seja, ele é a maior
distância entre qualquer par
de vértices. Para achar o
diâmetro de um grafo,
primeiro encontre o caminho
mínimo entre cada par de
vértices.
➤ O maior comprimento de
qualquer um desses caminhos
é o diâmetro do grafo.
V
W

83. DIÂMETRO
➤ O diâmetro de um grafo é a
excentricidade máxima de
qualquer vértice do grafo.
➤ Ou seja, ele é a maior
distância entre qualquer par
de vértices. Para achar o
diâmetro de um grafo,
primeiro encontre o caminho
mínimo entre cada par de
vértices.
➤ O maior comprimento de
qualquer um desses caminhos
é o diâmetro do grafo.
V
W
diam(G) = 5

84. CENTRO
➤ O Centro de um grafo G é o
subconjunto de vertices de
excentricidade mínima.

85. CENTRO
➤ O Centro de um grafo G é o
subconjunto de vertices de
excentricidade mínima.
Centro de G

86. ATIVIDADE
➤ Duplas
➤ Preparar uma apresentação sobre uma exemplo de
aplicabilidade da teoria dos grafos.
➤ Mostrar o problema real, explicar como modelar esse
problema real na forma de grafos.
➤ Mostrar “os ganhos” por utilizar teoria dos grafos nesse
problema.
➤ Preparar uma apresentação de 10 minutos.
➤ Apresentações na próxima aula!

87. REFERÊNCIAS
➤ Capítulo 1: Grafos : conceitos, algoritmos e aplicações (2012)
- Marco Goldbarg, Elizabeth Goldbarg.
➤ http://www.inf.ufsc.br/grafos/definicoes/definicao.html

88. TEORIA DOS GRAFOS
Victor Hazin da Rocha