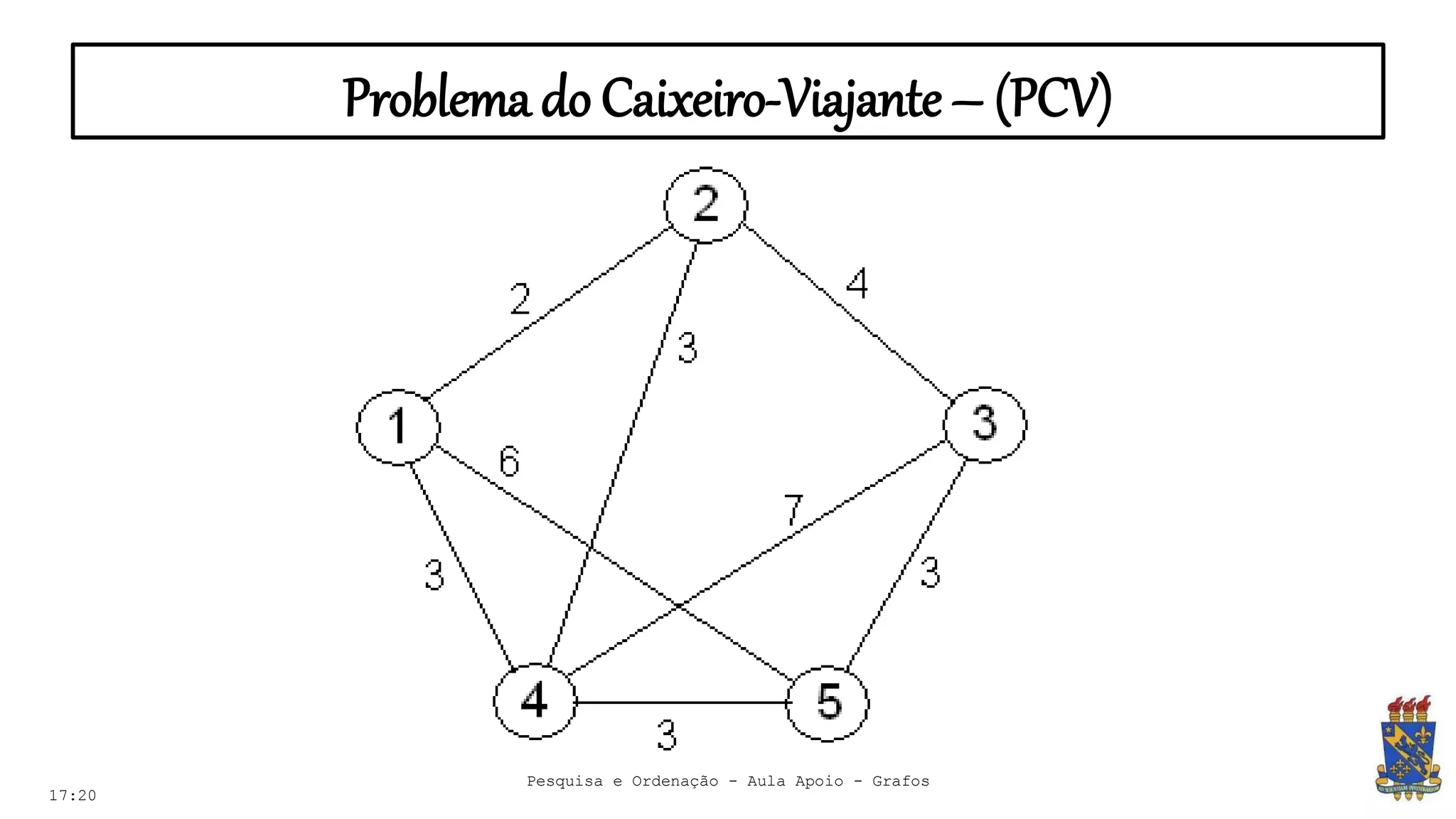
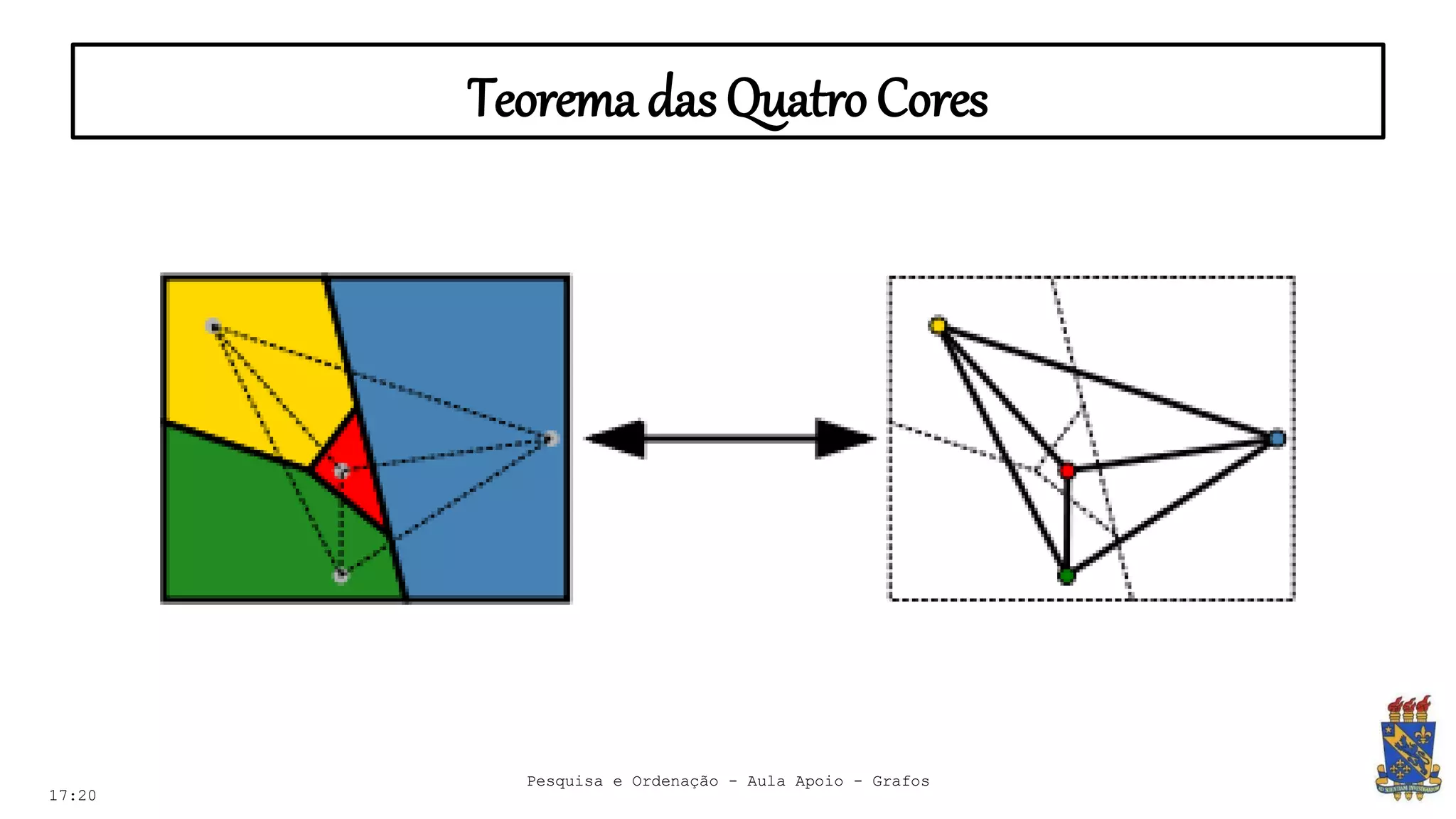
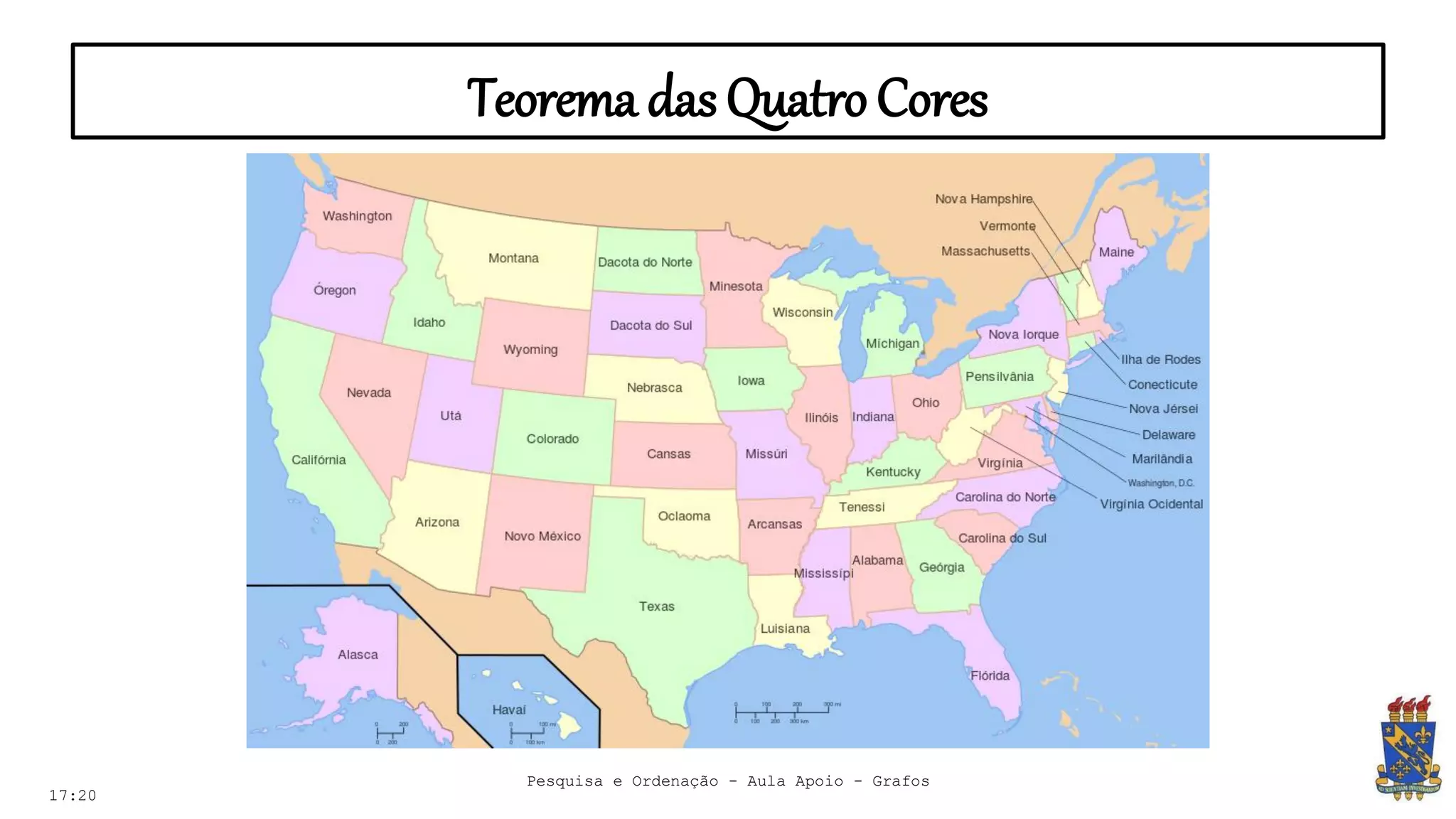
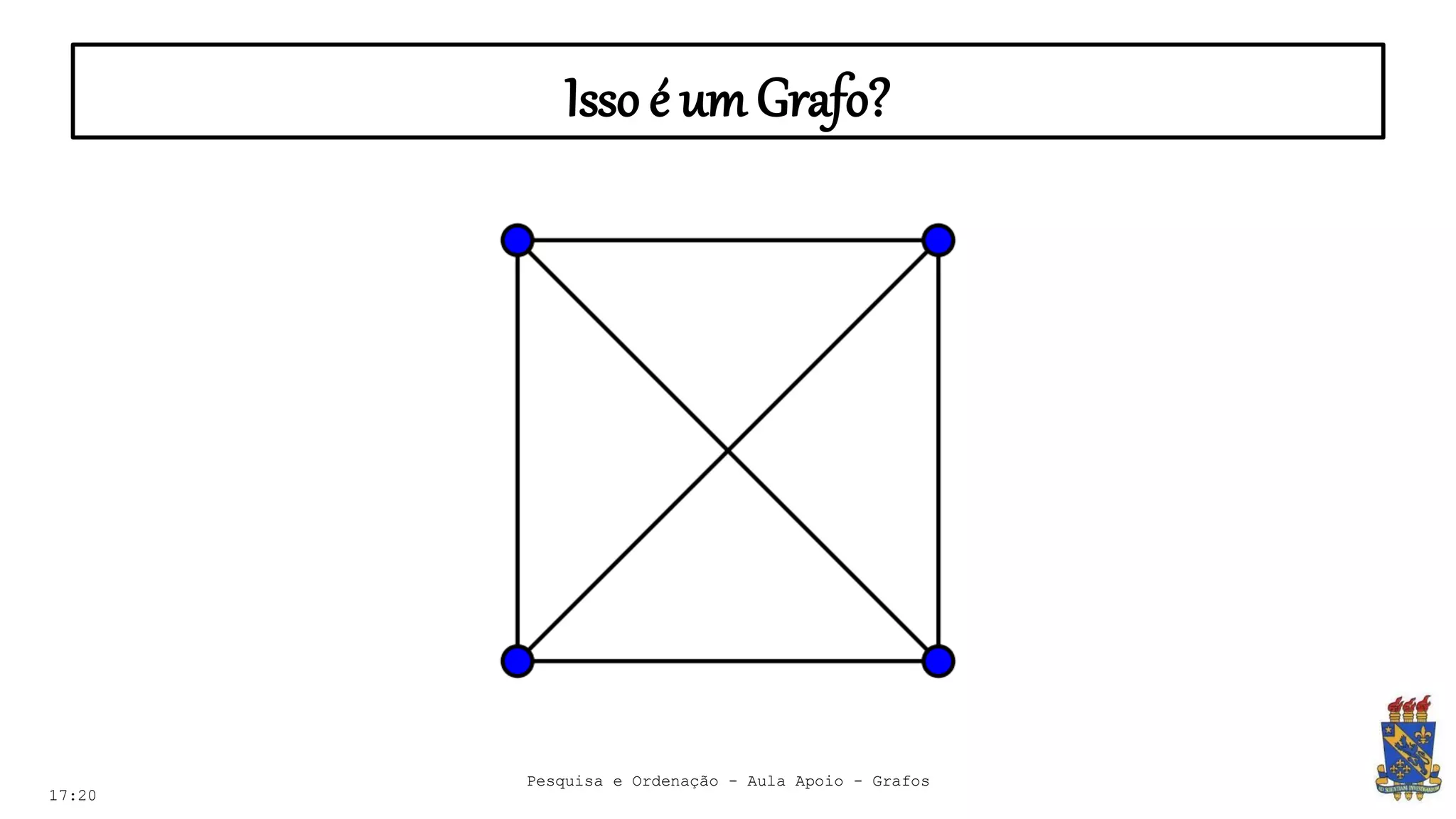
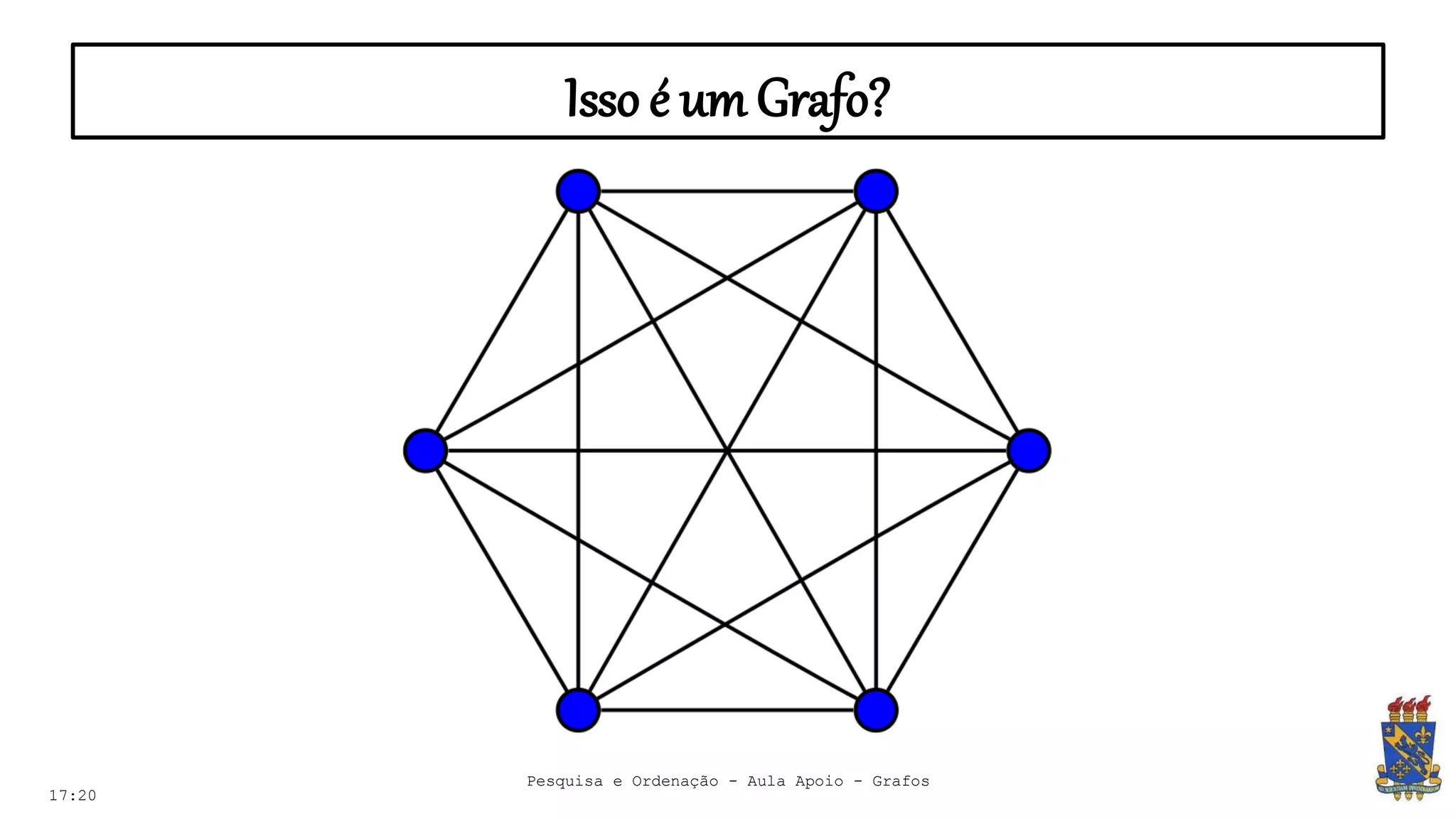
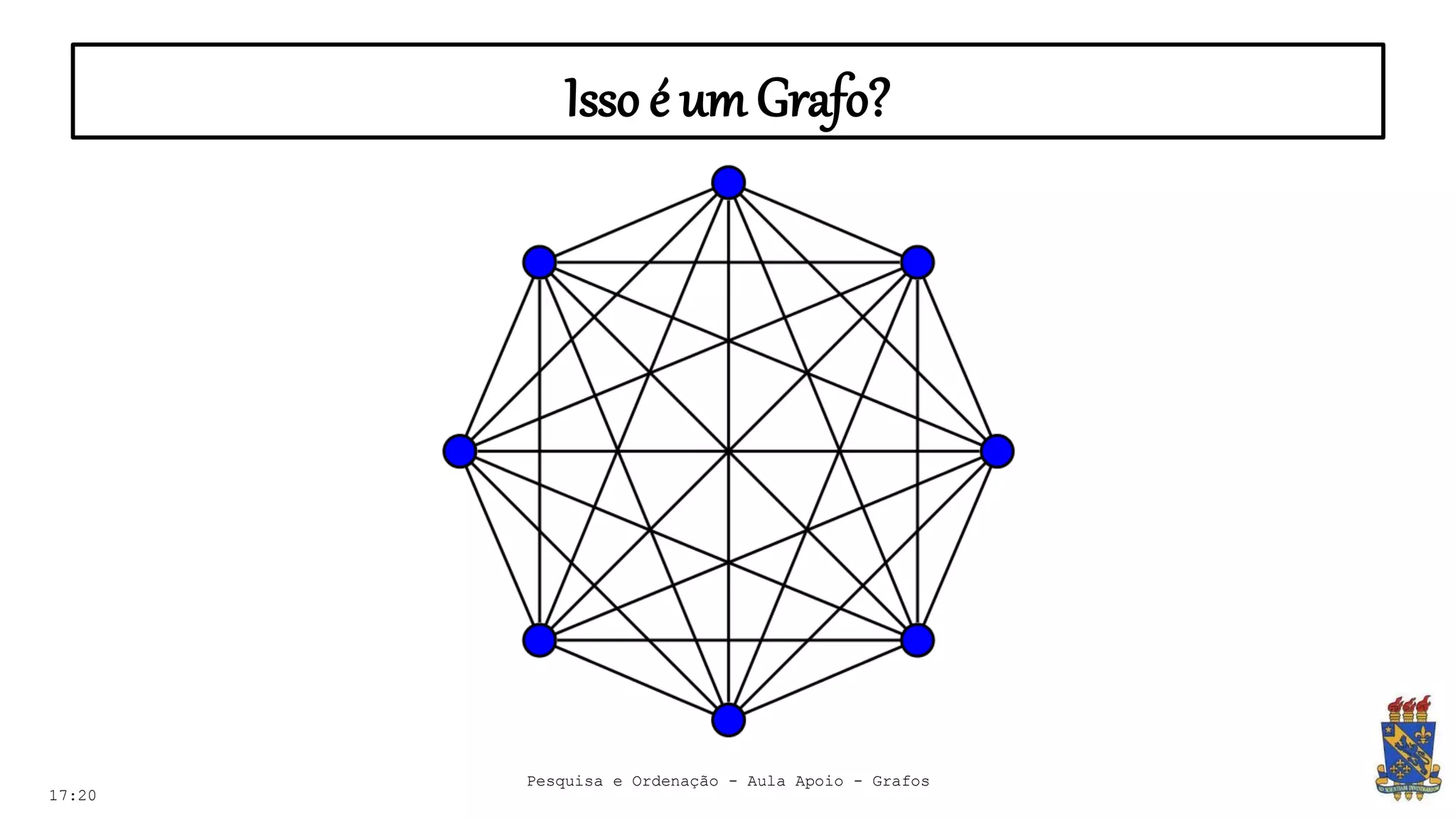
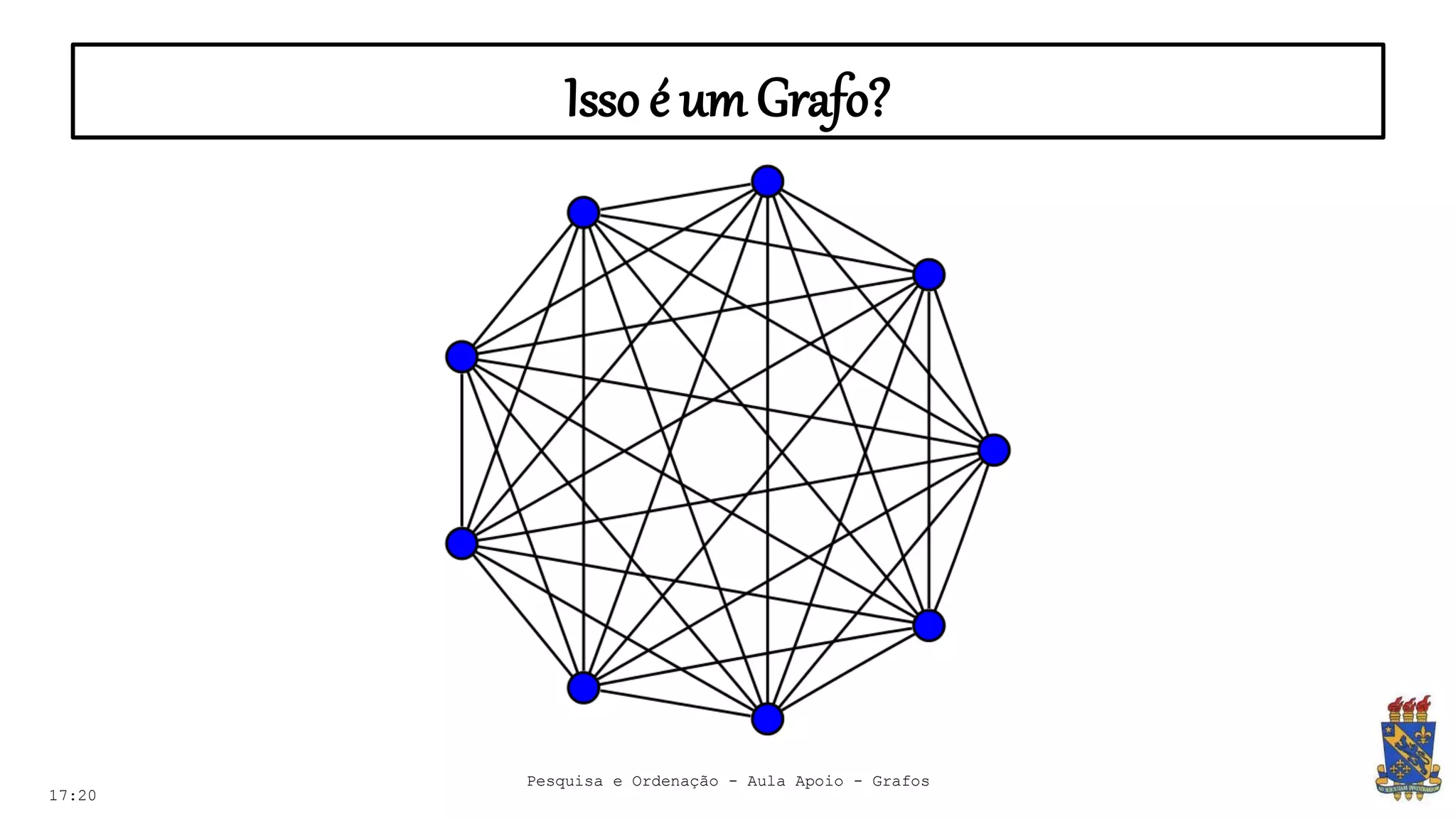
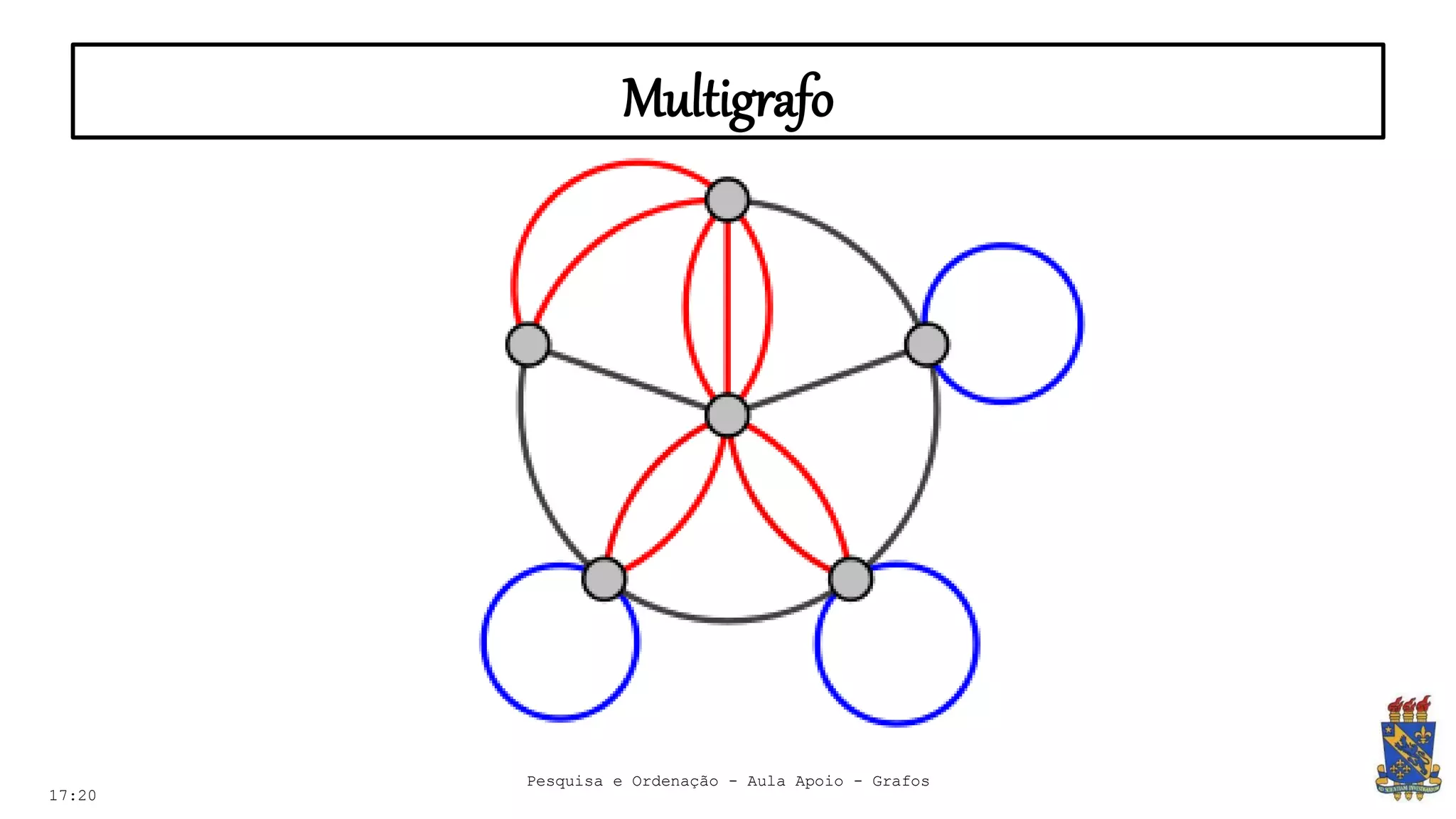
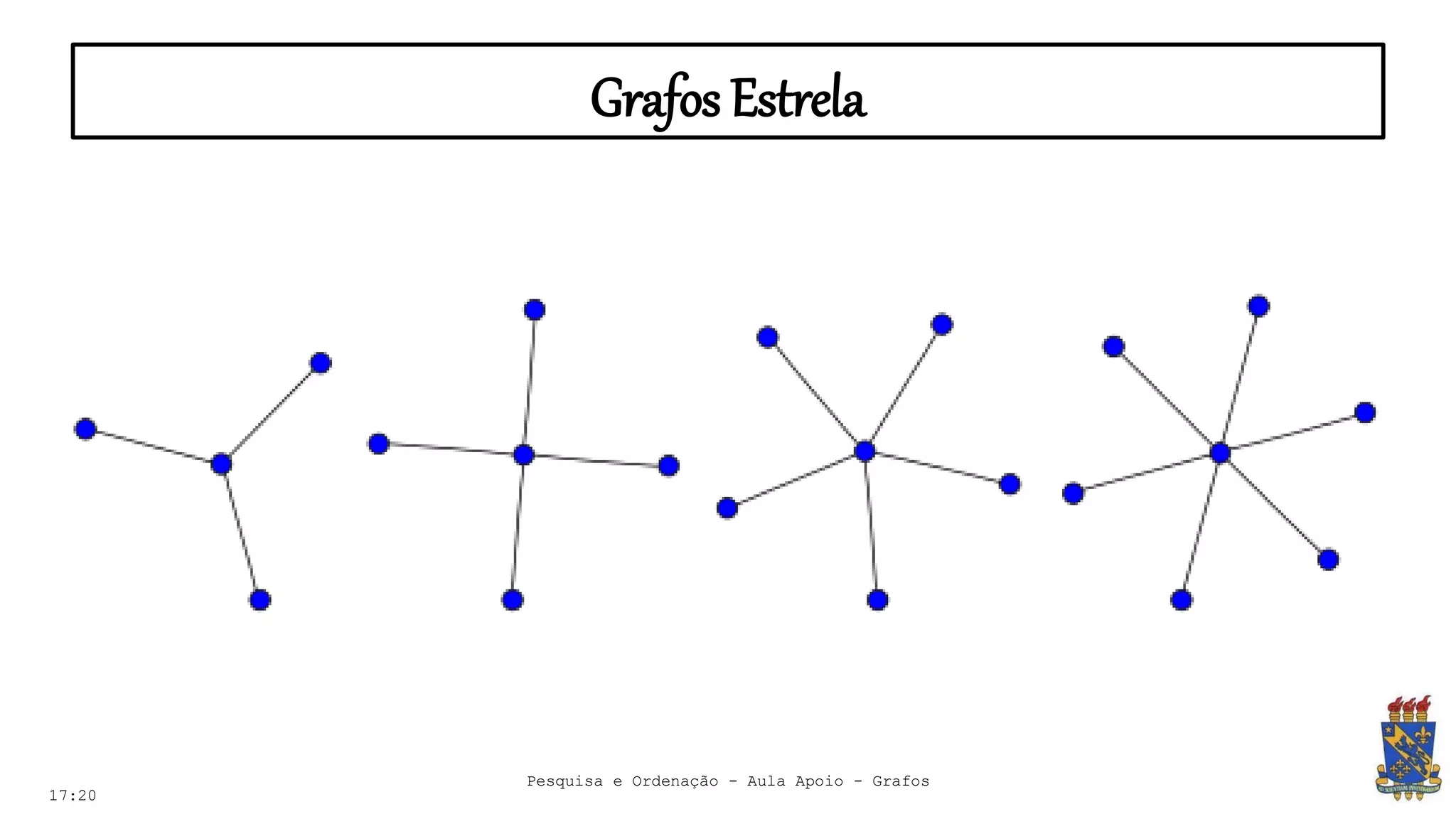
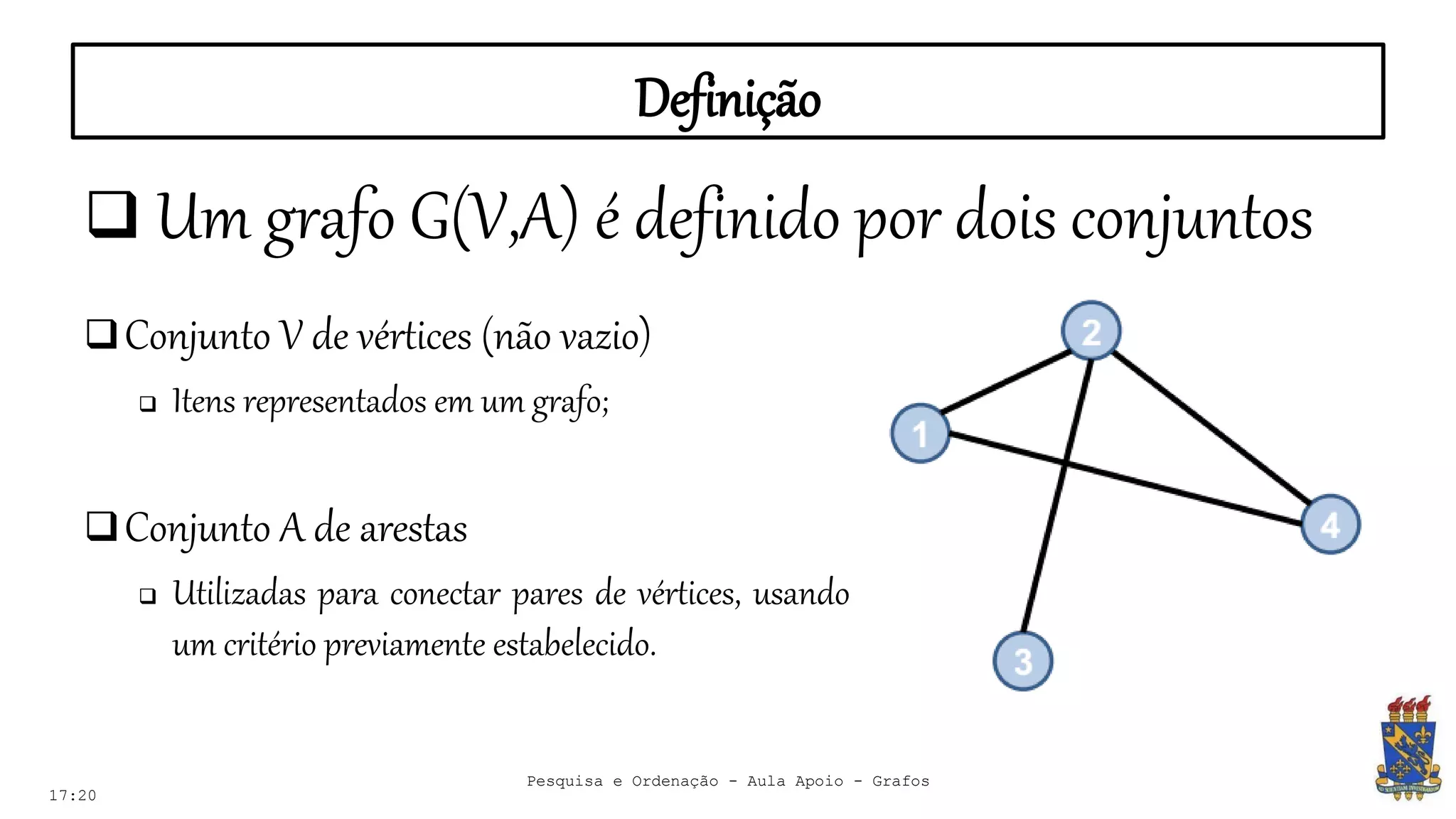
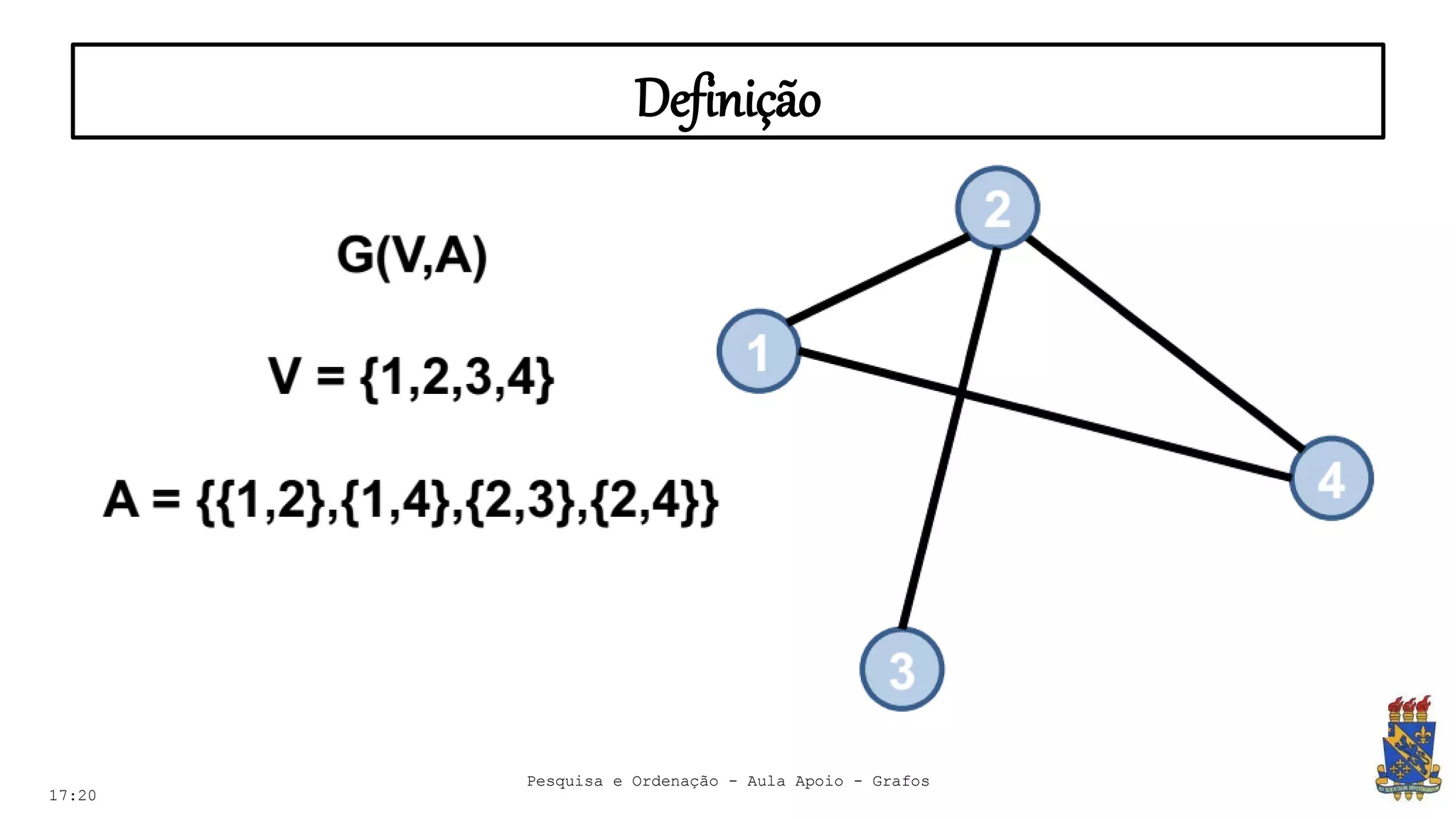
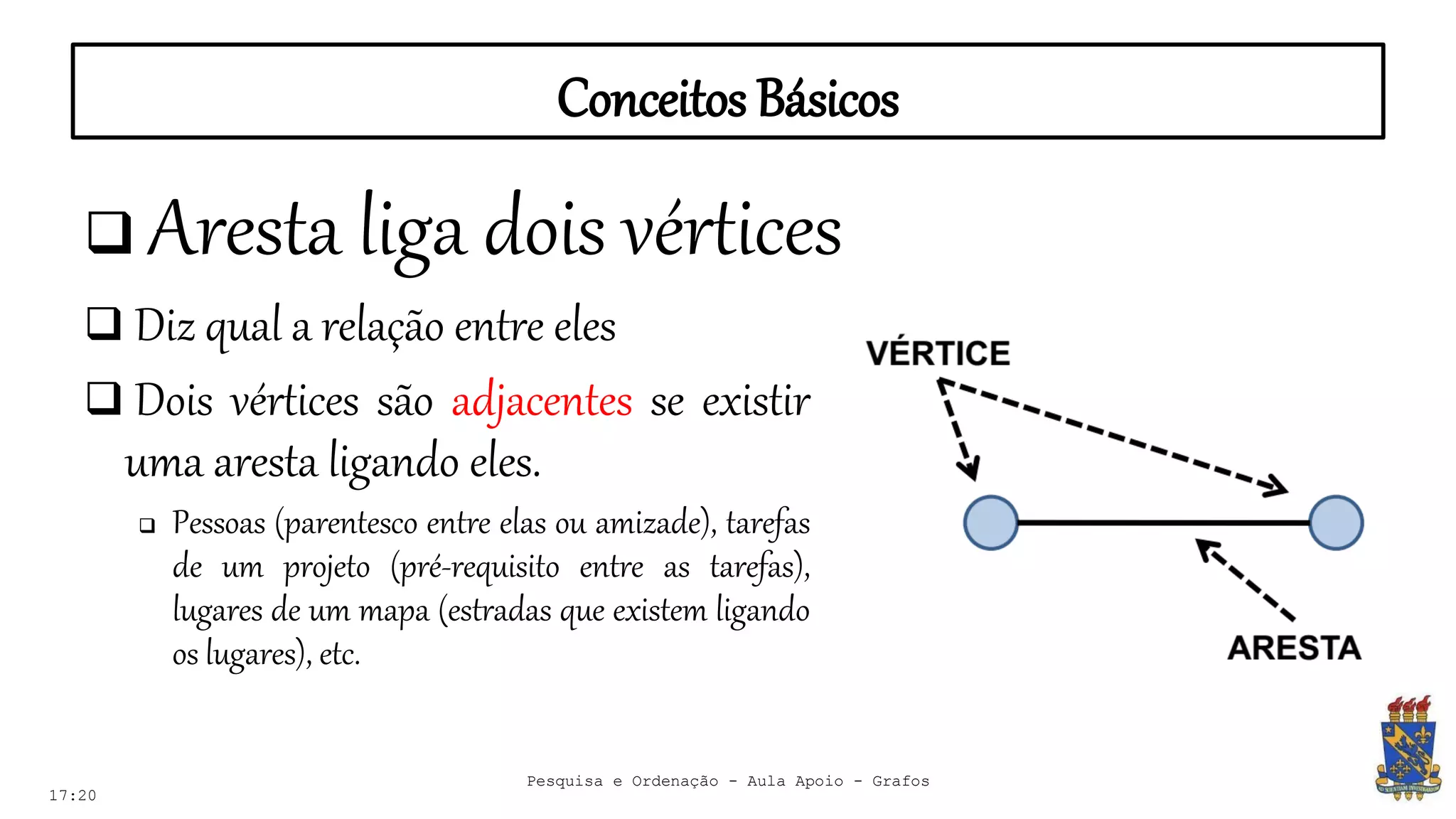
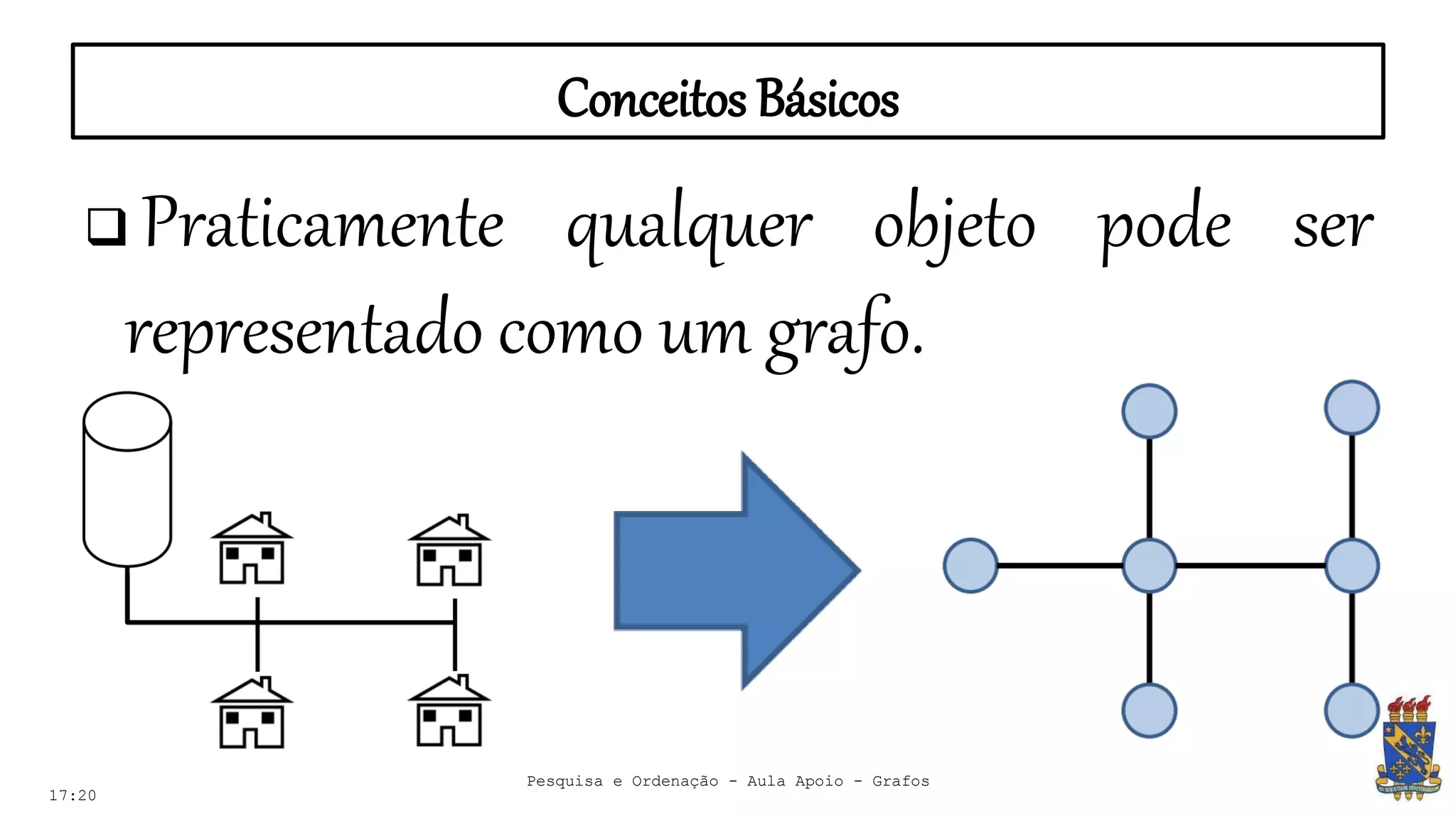
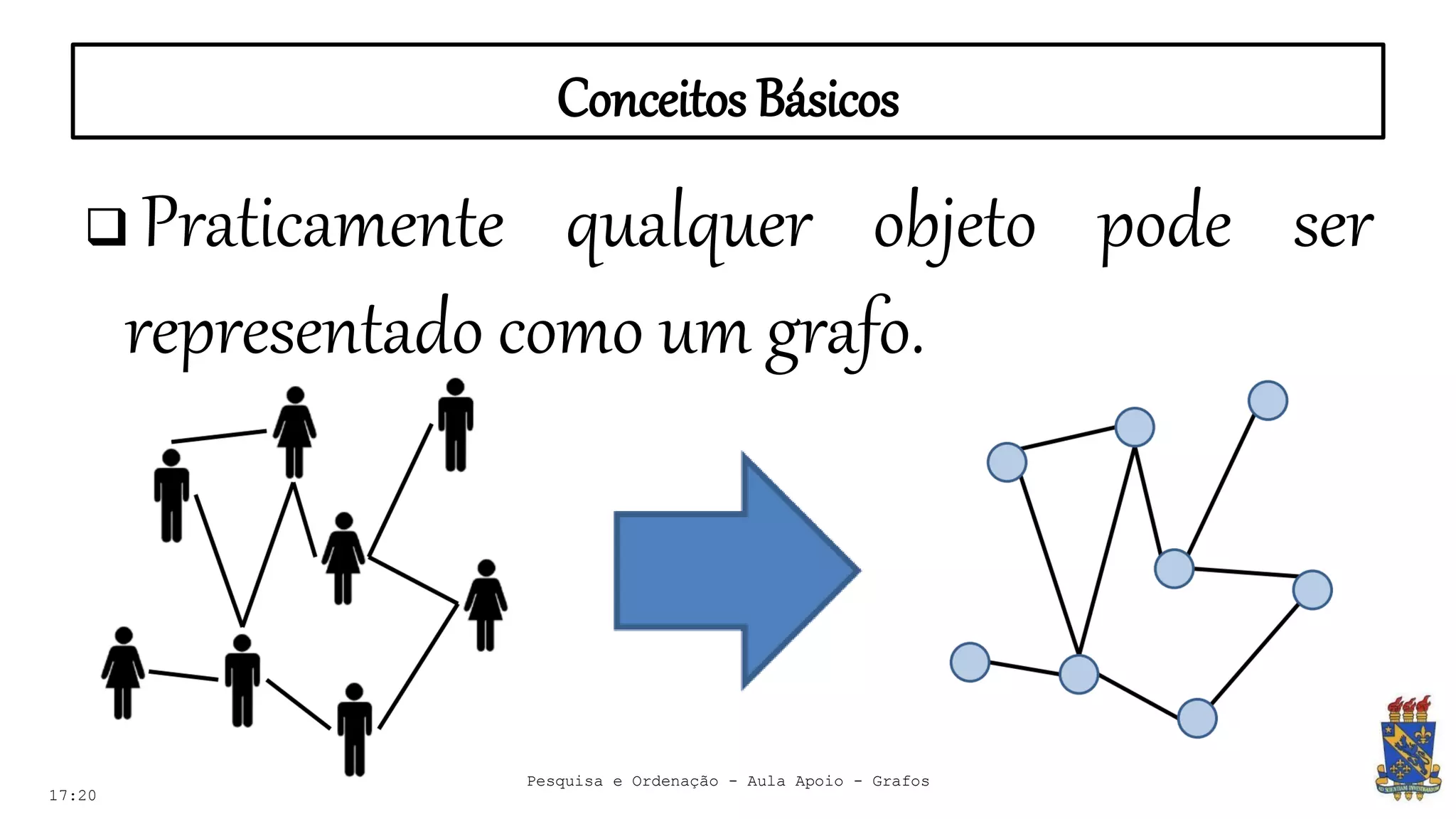
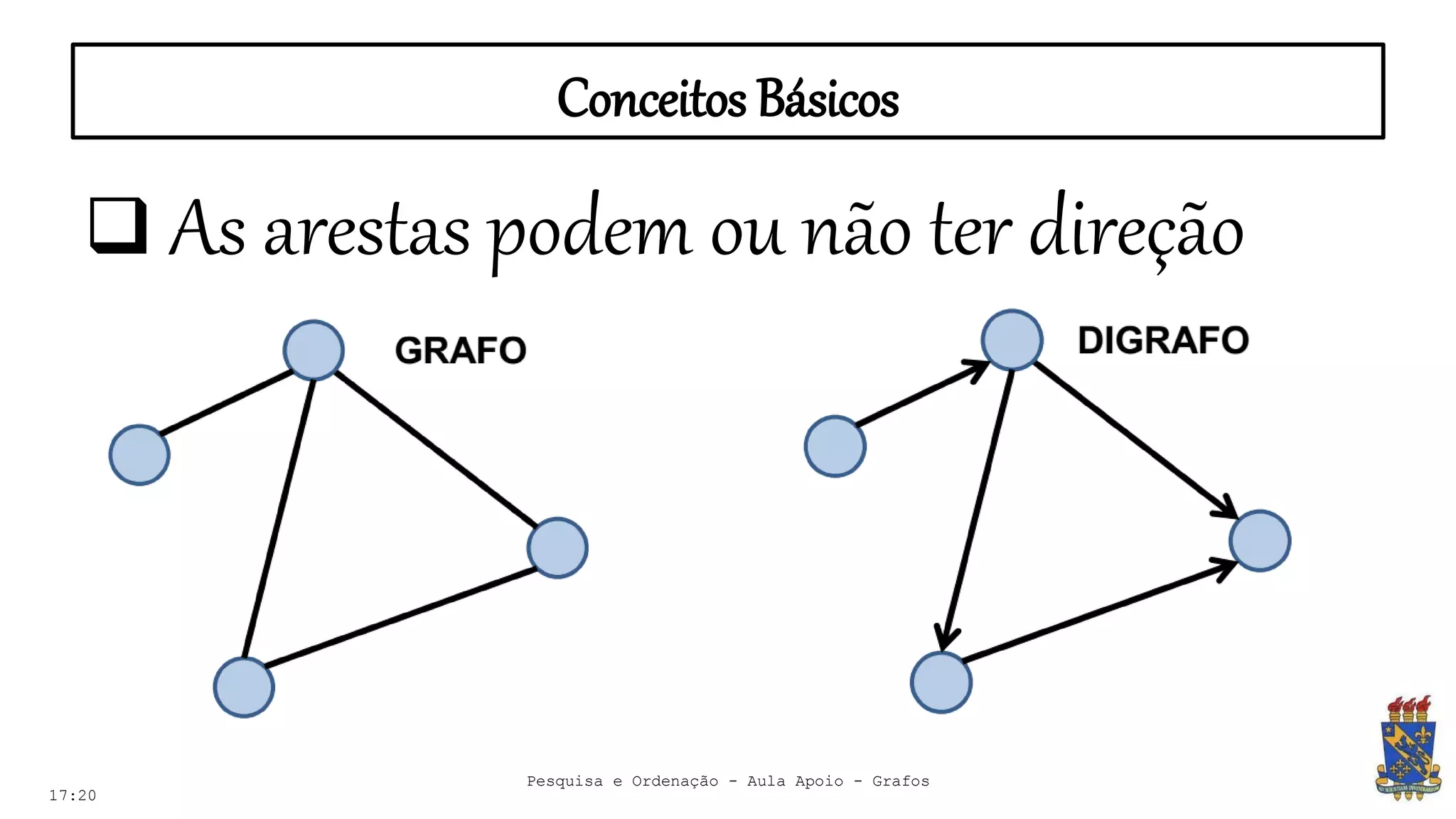
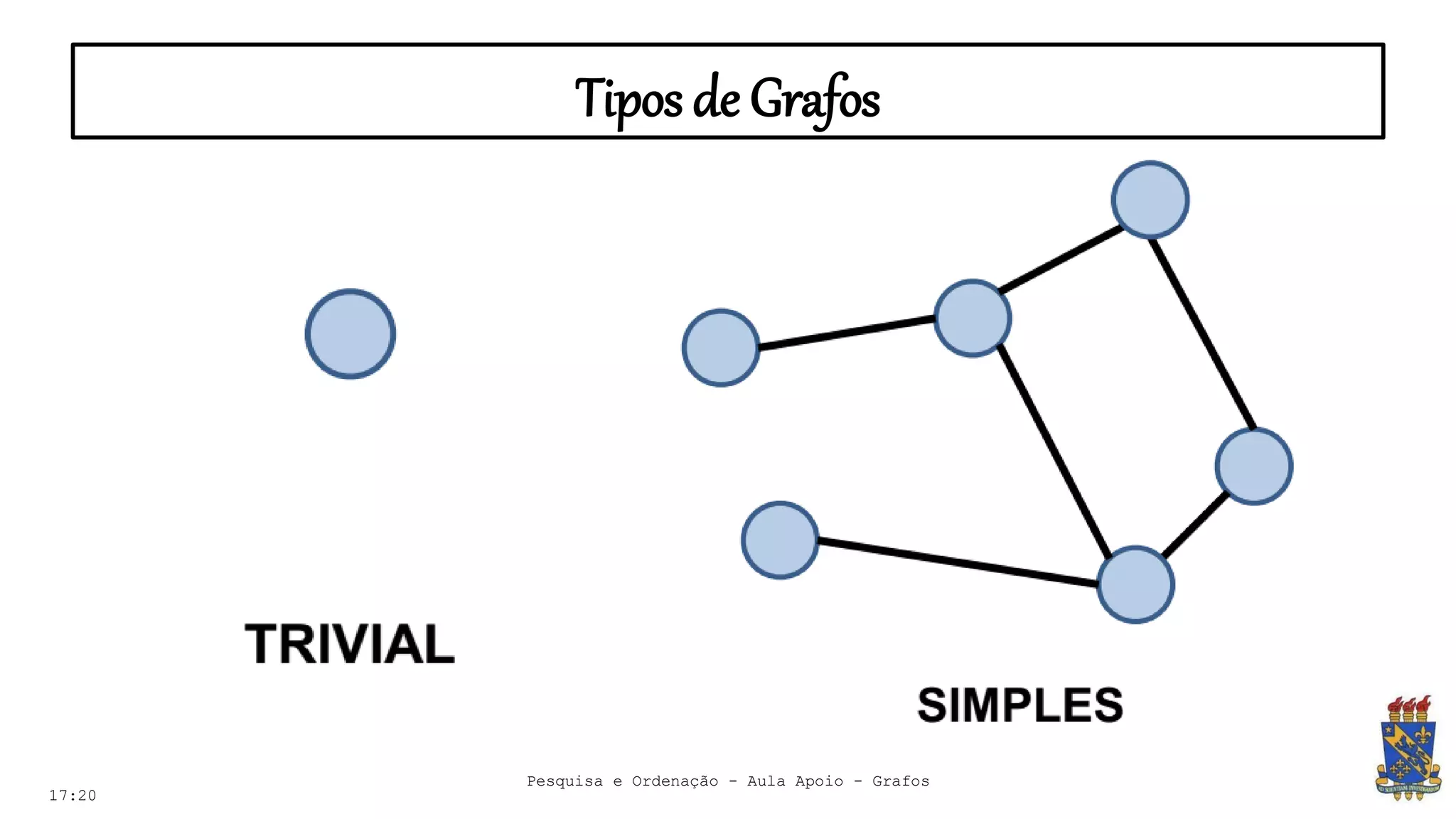
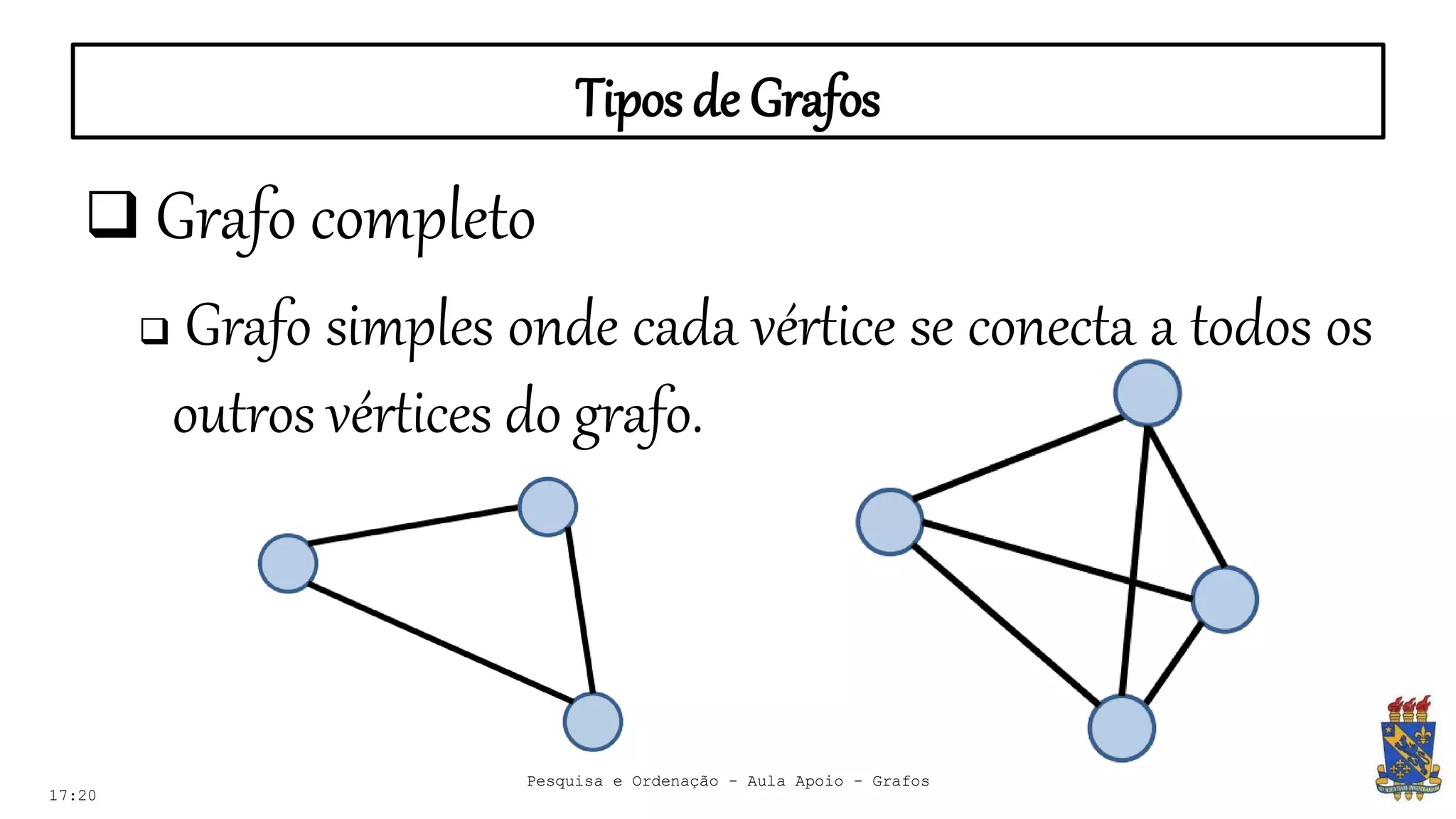
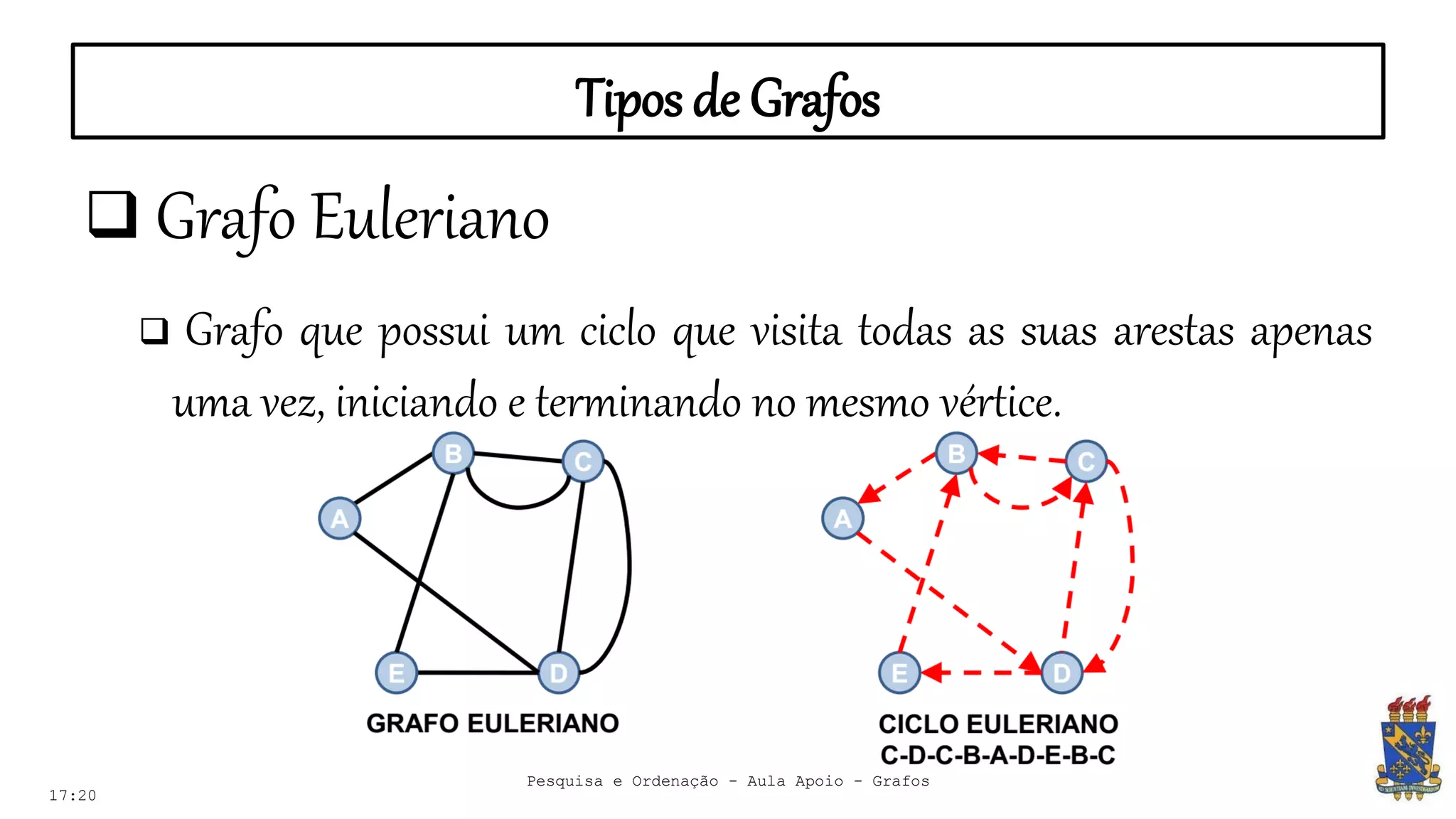
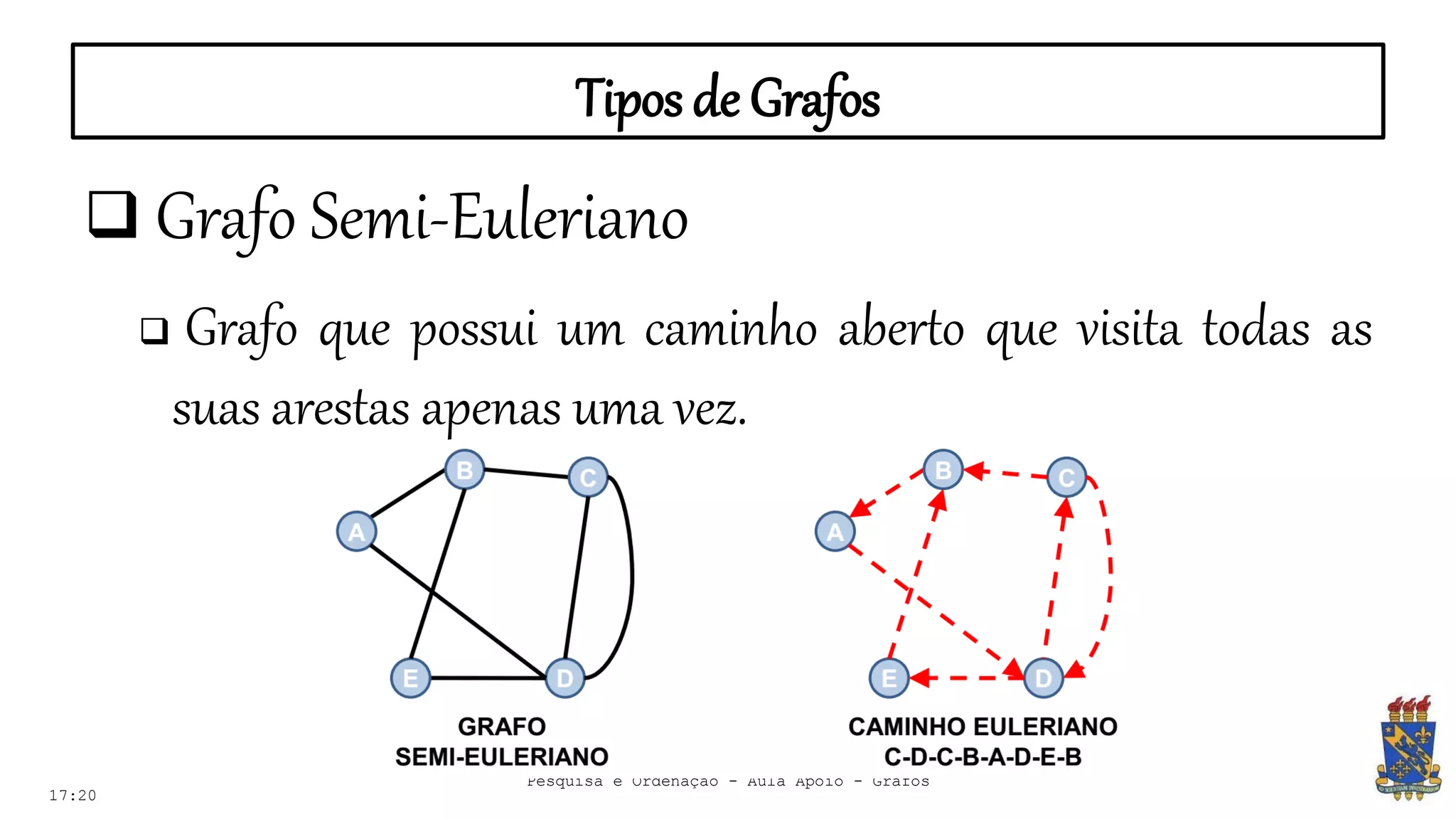
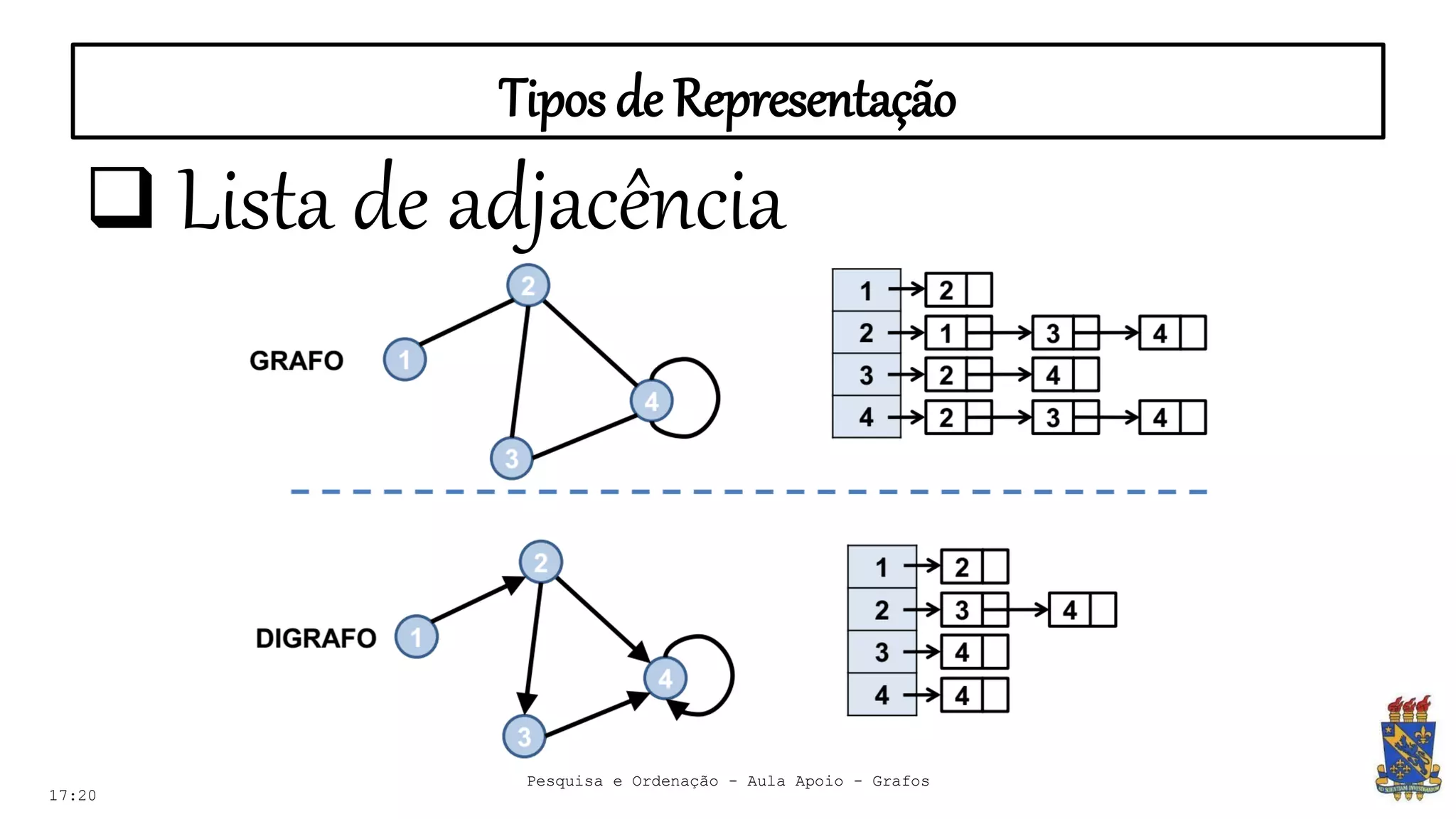
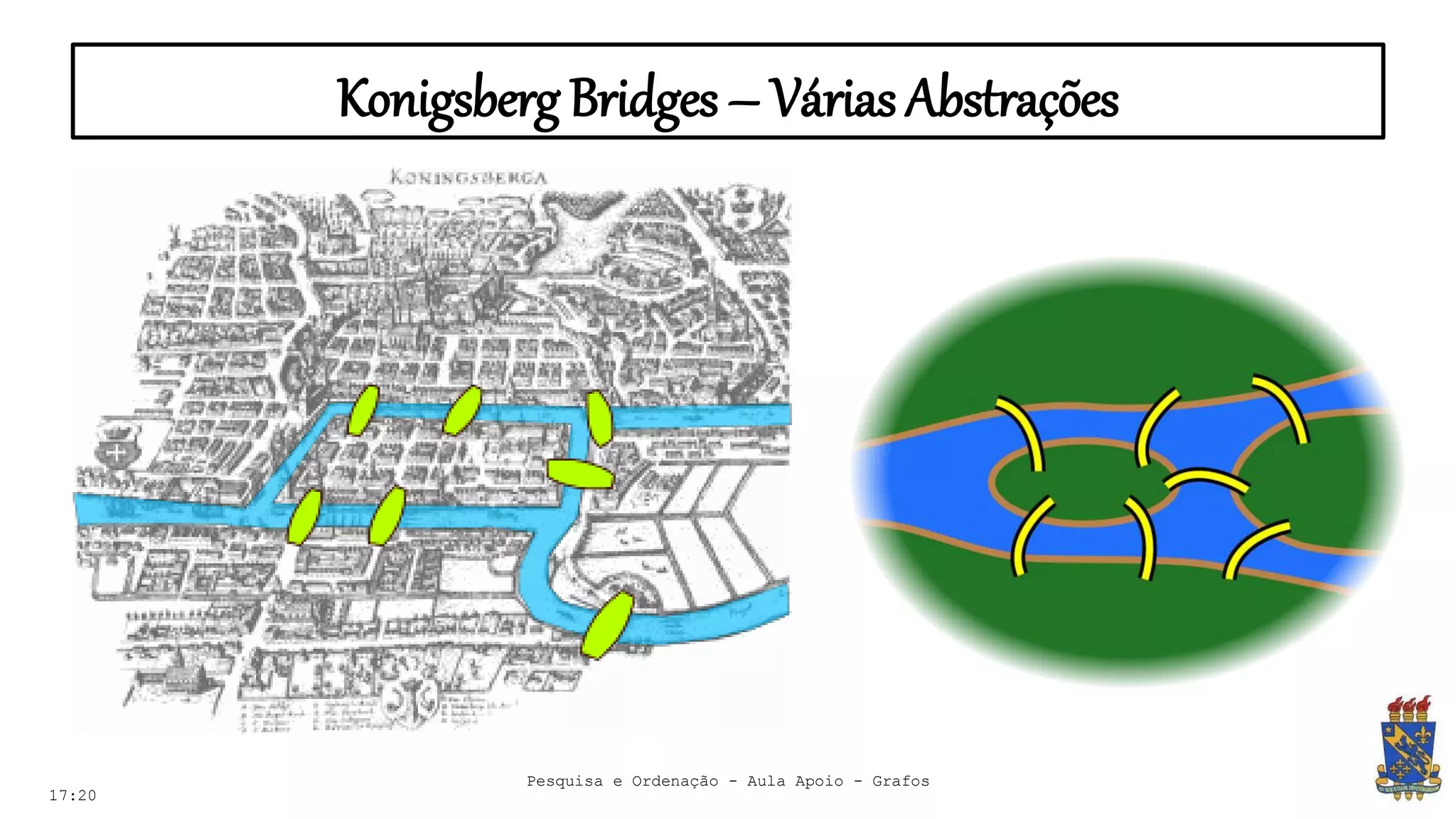
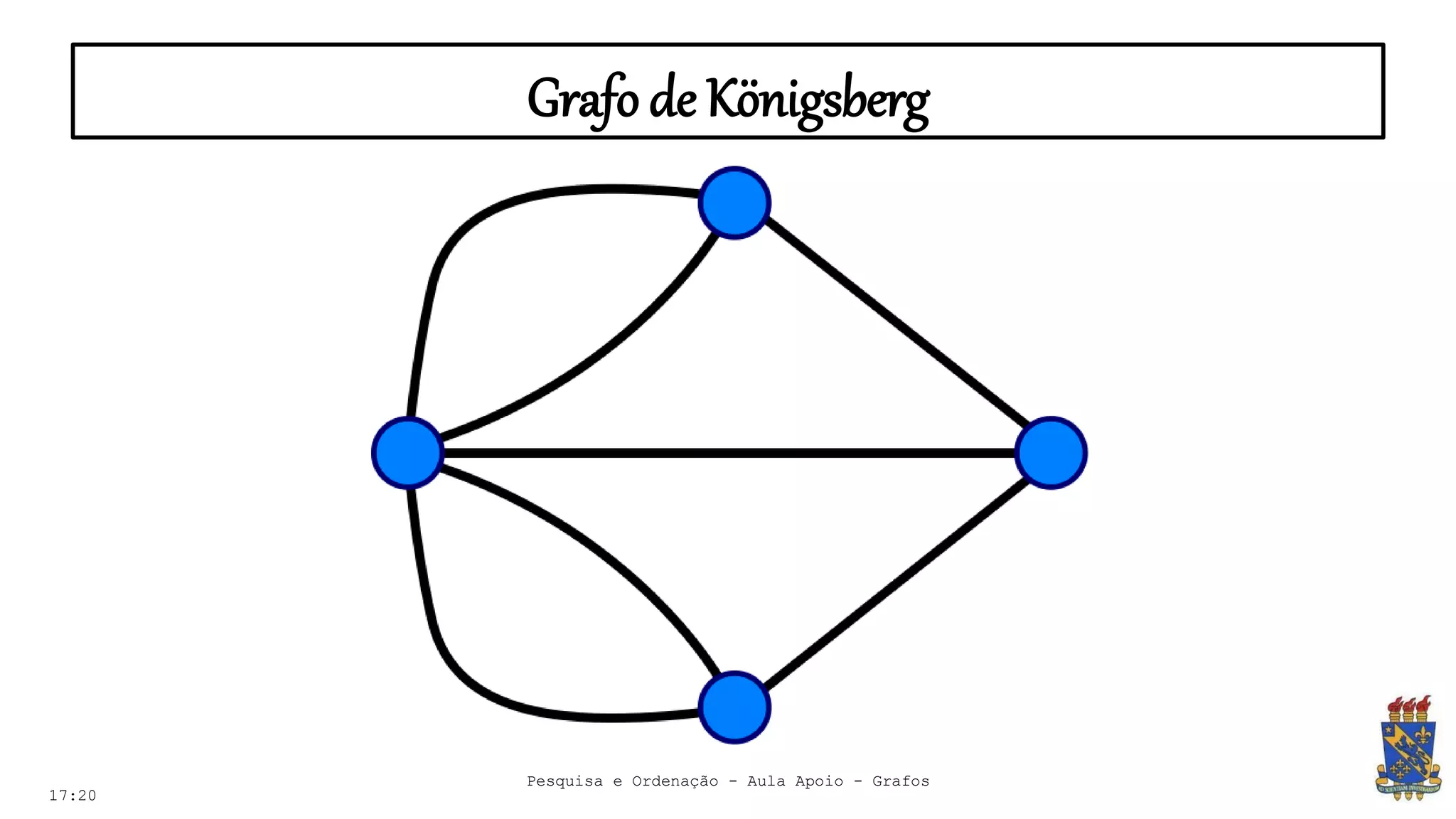
O documento discute grafos e sua representação em computação. Ele define grafos, apresenta conceitos básicos como vértices, arestas e grau. Também descreve tipos de grafos como completos, regulares e ponderados. Por fim, aborda formas de representar grafos no computador como matriz e lista de adjacência.





























![Neo4J
17:20
MATCH (keanu:Person { name:'Keanu Reeves' })-
[:ACTED_IN]-(movie:Movie)
RETURN movie
Pesquisa e Ordenação - Aula Apoio - Grafos](https://image.slidesharecdn.com/estruturadedados-aulaapoio-grafos-170207193013/75/Estrutura-de-Dados-Grafos-36-2048.jpg)

![ArangoShell
17:20
arangosh> var graph_module = require("org/arangodb/general-graph");
arangosh> var graph = graph_module._create("myGraph");
arangosh> graph;
[ Graph myGraph EdgeDefinitions: [ ] VertexCollections: [ ] ]
arangosh> graph._addVertexCollection("shop");
arangosh> graph._addVertexCollection("customer");
arangosh> graph._addVertexCollection("pet");
arangosh> graph
arangosh> var rel = graph_module._directedRelation("isCustomer", ["shop"], ["customer"]);
arangosh> graph._extendEdgeDefinitions(rel);
arangosh> graph;
[ Graph myGraph EdgeDefinitions: [
"isCustomer: [shop] -> [customer]"
] VertexCollections: [ ] ]
Pesquisa e Ordenação - Aula Apoio - Grafos](https://image.slidesharecdn.com/estruturadedados-aulaapoio-grafos-170207193013/75/Estrutura-de-Dados-Grafos-38-2048.jpg)
















































![Matriz de Adjacência
17:20
Pesquisa e Ordenação - Aula Apoio - Grafos
Uma matriz de adjacência é uma das formas de se representar um grafo.
Dado um grafo G com n vértices, podemos representá-lo em uma matriz 𝑛 𝑥 𝑛
𝐴(𝐺) = [𝑎𝑖𝑗] (ou simplesmente 𝐴).](https://image.slidesharecdn.com/estruturadedados-aulaapoio-grafos-170207193013/75/Estrutura-de-Dados-Grafos-100-2048.jpg)